220414_TIL / (Scree plot, K-mean Clustering)

어제 eigenvercotr, eigenvalue, PCA에 워낙 뚜드려 맞아서인지, 오늘 배운 것은 그래도 괜찮게 느껴졌다. 😆 오늘 배운 개념 및 파이썬으로의 구현에 대한 기록을 남겨둔다.

Key words

• Scree plot
• K-mean Clustering (오늘의 Main)

---

# Scree plot

어제 PCA에 대해서 배웠다. PCA를 할 때 원 데이터의 정보를 가장 잘 보존하고 있는 PC만을 사용하며 차원축소를 한다고 했는데, 그럼 이런 궁금증이 들 수 있을 것이다.

PCA를 통해 몇 차원으로 축소하는게 좋을까?
(= 몇 개의 PC를 사용하는 게 가장 좋을까?)

바로 그럴 때 활용할 수 있는 것이 바로 Scree Plot이다.

Scree Plot의 예시를 한 번 보자.

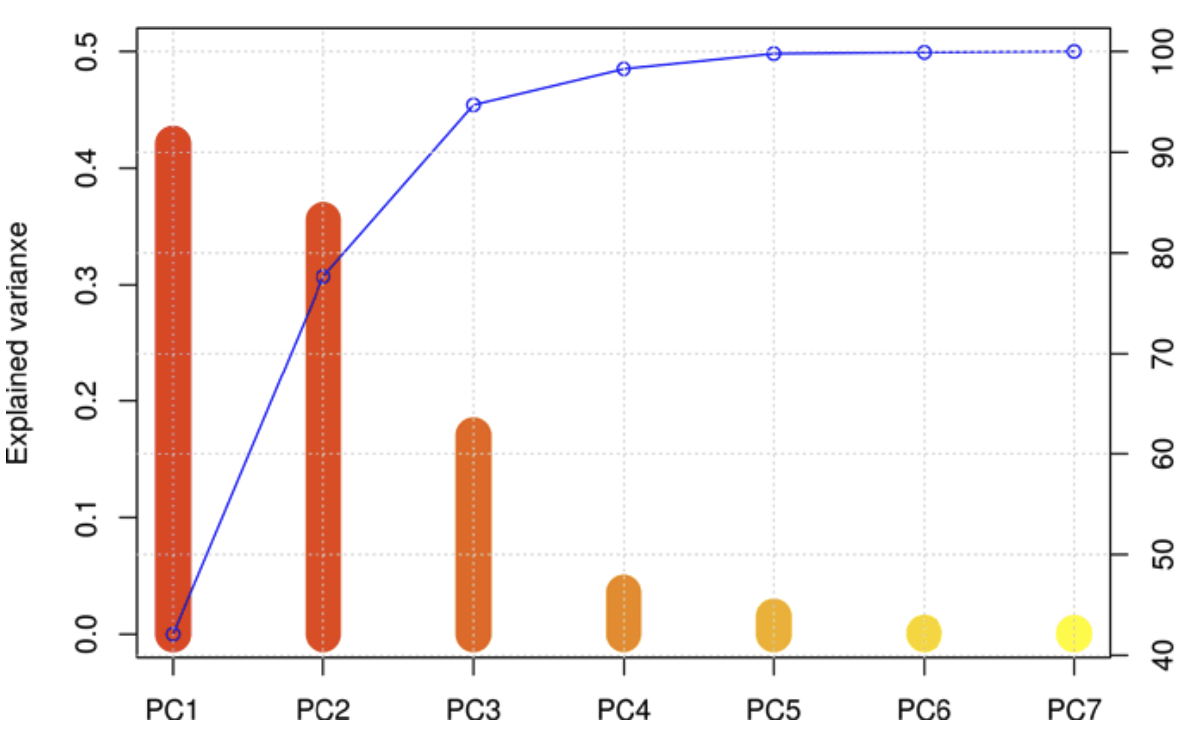
각 PC별로 Explained Variance 즉 Eigenvalue값이 얼마나 나오는지를 보여준다. 선은 누적 값을 나타낸 것이다.

해석은 이렇게 하면 된다.

• PC1이 전체 분산에서 40% 정도를 가지고 있고, PC2는 약 35% 정도를 차지하고 있다.
  • 둘의 누적은 75%이다. (즉, 2차원으로 축소한다면 정보의 손실이 약 25% 정도는 발생할 것이라고 예상할 수 있다.)
• (통상적으로 70~80% 정도만 되어도 괜찮은 것으로 본다고는 하한다는데..) 위 그래프의 경우에는 누적 분산이 완만해지는 PC3까지는 사용해야 데이터의 특징을 가장 잘 담고 있겠구나~ 주성분 3개를 쓰자~ 는 식으로 판단할 수도 있다.

몇 개의 주성분을 선택할지 무조건 옳다고 정해진 답은 없겠지만, scree plot을 통해 판단에 도움을 받을 수 있다니 흥미롭다.

# K-mean Clustering

K-mean Clustering은 비지도 학습(Unsupervised Learning)의 대표적인 기법 중 하나이다. 어제 배운 PCA도 비지도 학습의 하나인데, 데이터를 압축하거나 군집화, 시각화를 통해 데이터의 특징을 찾기 위해 쓰인다고 생각하자.

K-mean Clustering이 뭔지를 시각적으로 이해하기에 정말x100 좋은 사이트가 있다. 사실 여기 들어가서 몇 번만 돌려보면 K-mean Clustering이 뭔지 단번에 이해가 될 것이다.

간단히만 프로세스를 요약해서 말해보자면

1. K개의 random point를 찍어 각 cluster의 중심점으로 설정한다.
2. 각 cluster 중심점(아까 찍은 임의의 point)에 근접해 있는 데이터끼리 묶는다.
3. 각 cluster의 중심점(이때는 mean)을 새로 찾아 설정한다.
4. 새로 설정된 중심점(centorid point)을 기준으로 근접해 있는 데이터끼리 다시 묶어 나눈다.
   -유의미한 변화가 없을 때까지 3, 4를 반복한다.

다시 한번 강조하지만 위 사이트 링크에 들어가서 직접 돌려보는 걸 강력히 추천한다!

처음에 K개의 random point를 찍어주었는데, 그럼 몇 개로 하는게 좋을까?

물론 도메인 지식이 있다면 그걸 바탕으로 정해도 된다. 하지만 그렇지 않다면, 수학적으로는 Elbow Method라는 방법을 통해 도움을 받을 수 있다.

Elbow Method는 Cluster의 개수를 1개, 2개, 3개 .. 차례로 늘리면서, Cluster 간 거리의 합을 나타내는 inertia가 급격이 떨어지는 구간을 찾아내서, 초기 K값을 설정하는데 도움을 주는 방법이다. (말보다는 이 영상을 보면 더 쉽게 이해할 수 있다.)

• 예시를 보자.
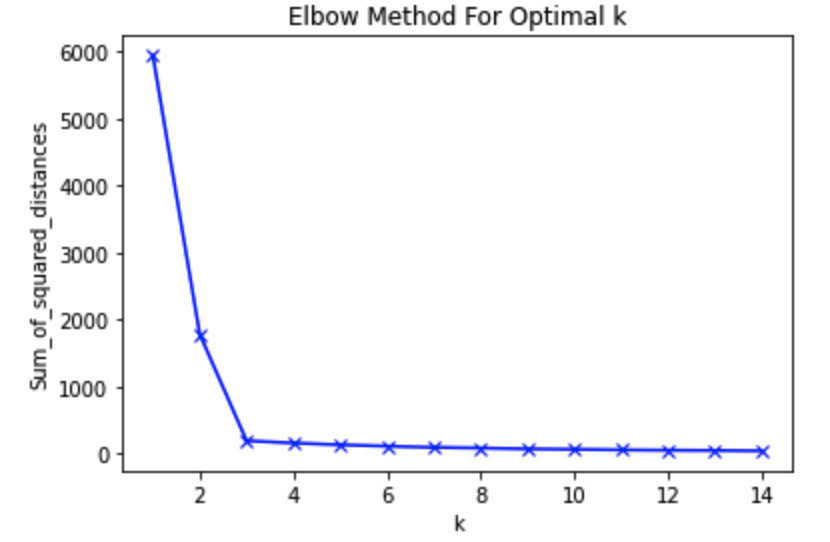
• 위를 보면 3개의 Cluster를 넘었을 때 데이터 간 거리의 변화가 작아진다. 그럼 K는 3으로 설정해서 K-mean Clustering 돌려보자~ 라고 판단할 수 있는 것이다.

잠깐. 그럼 K값 그냥 맘대로 해도 되는거 아냐? 왜 굳이 이래야하지? 라고 한다면,

K-mean Clustering은 단점도 있다.

초기에 K개의 임의의 중심점(centroid)를 찍고 그걸 바탕으로 쭉 클러스터링이 진행되다보니, 이 초기의 centroid에 따라 클러스터링의 영향이 안 좋거나, 끝없이 반복해야 하는 경우도 있다.

예시를 보자.

• 
• 위 추천 사이트에서 돌려본 것인데, 초기 중심점 설정에 따라 클러스터링이 이렇게도 일어날 수 있다. 사람이 보면 저렇게 클러스터링이 되면 안될 것이 딱 보인다고 해도 말이다.

당연히 초기에 K를 몇 개로 지정해주느냐에 따라 클러스터링의 결과가 영향을 받을 수도 있을 것이다.

파이썬에서 해보자

개념에 대해서는 정리가 된 것 같고, 이제 파이썬에서 K-mean Clustering을 어떻게 하는지 기록해둔다.

캐글의 이 데이터셋이다.

이 데이터셋에는 이미 Diagnosis라는 라벨 칼럼이 있다. K-mean Clustering을 해서 원래의 라벨과 얼마나 차이가 나는지를 보는게 목표다.

초기에 데이터를 불러오는 과정은 생략한다.

먼저 데이터를 표준화 해준다.

• 데이터 간 특성이 다른 경우 표준화 해주는 것을 잊지 말자.
  (예를 들어, kg, cm 정보가 같이 있다면 이걸 표준화해줘서 같이 비교할 수 있게 하는 것이다)

#Diagnosis lable
label = df[['diagnosis']] #원래 라벨 정보는 따로 저장해둔다.

#StandardScaler
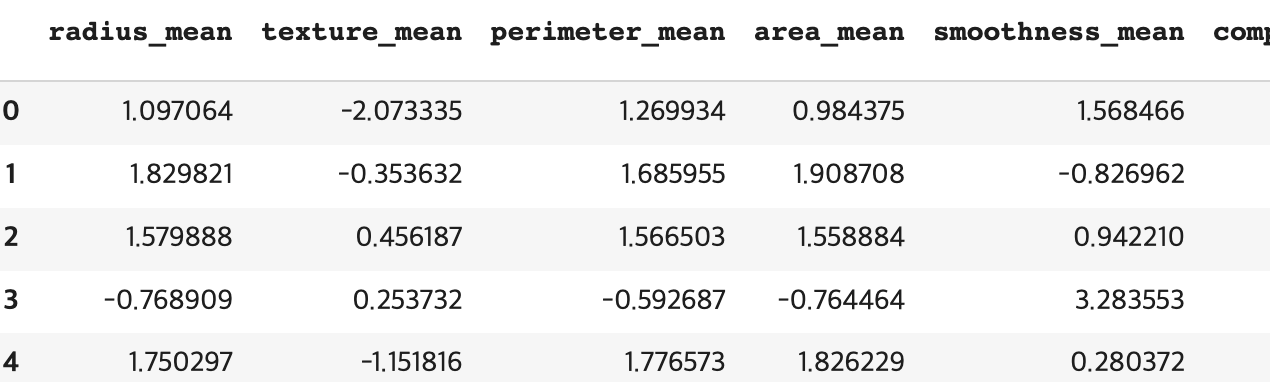
std_feature = df.loc[:, 'radius_mean': 'fractal_dimension_worst'] #diagnosis를 보는데 의미있는 칼럼들만 준비

scaler = StandardScaler()
stded = scaler.fit_transform(std_feature) 
std_df = pd.DataFrame(stded, columns = df.columns[2:32])

output

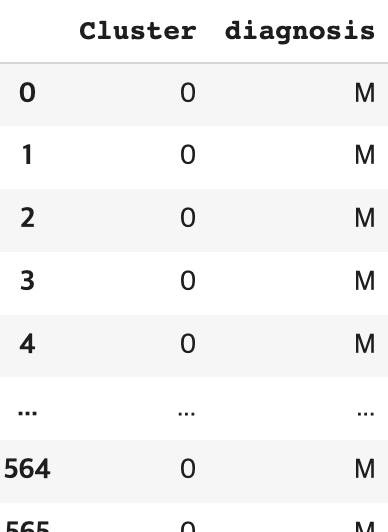
K-mean Clustering

#k-mean clusterting
kmeans = KMeans(n_clusters = 2, random_state = 42)
kmeans.fit(std_df)
labels = kmeans.labels_

#labels dataframe 변환
label_df = pd.DataFrame(labels)

#std_df에 라벨 데이터 추가. 
std_df['Cluster'] = label_df

#Cluster, Diagnosis 데이터만 'df' 할당
df = pd.concat([std_df['Cluster'], label], axis = 1)
df

output

• 

이제 원래 Diagnosis 라벨과 비교를 해보자.

# 분석하기 쉽게 df['cluster']를 M, B로 바꾸자.

df['Cluster'] = df['Cluster'].replace(0,"M")
df['Cluster'] = df['Cluster'].replace(1,"B")

#두 칼럼의 값이 일치하는지를 알 수 있도록 칼럼을 추가하자.
same_or_not = []

for i in range(0, 569):
  if df['Cluster'][i] == df['diagnosis'][i]:
    same_or_not.append(1) # 두 값이 일치하면 숫자 1을 추가한다. 
  else:
    same_or_not.append(0) # 두 값이 일치하지 않으면 숫자 0을 추가한다. 

same_or_not_df = pd.DataFrame(same_or_not)

new_df = pd.concat([df, same_or_not_df], axis = 1)

# 최종
Acc = same_or_not_df.sum() / len(new_df.index)
Acc #0.910369 91% 정도 나온다. 

마지막에 flatten 함수를 이용해서 하는 방법도 있는 것 같은데, 나한테는 위처럼 하는게 더 직관적으로 다가오는 것 같다.

---

오늘도 재밌었다!