오늘은 어제에 이어 선형대수 두 번째 시간이다.
중요한 개념들이지만 마찬가지로 아주 헷갈릴 수 있는 부분인 것 같다. 한 달 뒤의 내가 기억할 수 있도록 날 도와줘 TIL!
Key words
- Covariance (공분산)
- Correlation coefficient (상관 계수)
- Orthogonality (직교성)
- span (⭐)
- rank
공분산 보기 전에 기본 개념부터 챙겨보자!
분산이란?
- 데이터가 흩어진 정도로, 각 값들의 평균과의 차이(=편차)의 제곱의 평균이다.
- 파이썬에서는
np.var()를 통해 계산할 수 있다.
표준 편차란?
- 분산에 루트를 씌운 것이다. 왜?
- 분산 계산할 때 제곱을 하기 때문에, 데이터의 스케일에 따라서 같은 퍼짐이어도 분산 값이 크게 차이가 날 수도 있기 때문이다.
- 이 스케일의 차이를 줄여주기 위해서 루트를 씌워서 보려는 것이다.
- 이 분산과 표준편차의 관계는 공분산과 상관계수의 관계와 똑같다.
- 파이썬에서는
np.std()를 통해 계산할 수 있다.
공분산이란?
한 개의 변수 값이 변화할 때 다른 변수가 어떤 연관성을 가지고 변화하는지를 측정하는 값이다.
- 수학적인 식으로는, x의 편차와 y의 편차를 곱한 것의 평균이다.
- : x가 증가할 때 y는 감소한다.
- : 뚜렷한 연관이 없다.
- : x가 증가할 때 y도 증가한다.
- 파이썬에서는
df.cov(x, y)를 통해서 구할 수 있다.-
예를 들어,
[243, 278, 184, 249, 207],[88, 89, 83, 112, 104]이 둘의 공분산을 구하려 한다면,#df 준비 df = pd.DataFrame({'a':[243, 278, 184, 249, 207], 'b': [88, 89, 83, 112, 104] }) df.cov()이렇게 간단히 구할 수 있다.
-
나온 결과 해석하는 것도 한 번 보자.

-
이걸 해석할 때는 a와 a의 공분산이 1363.7, a와 b의 공분산이 71.7이라고 하면 된다. (a와 a의 공분산이라 하면 그냥 a의 분산이다)
-
상관계수
공분산도 데이터 스케일의 영향을 받는다.(즉, 2개의 데이터 셋이 동일한 연관성을 가진다고 해서 공분산의 값이 반드시 동일한 것은 아니다) 이걸 보정하기 위해 사용하는 것이 바로 상관계수다. (따라서 상관계수는 데이터의 평균 혹은 분산의 크기에 영향을 받지 않는다)
- -1 ~ 1 사이의 값이다.
- 수학적으로는 공분산을 두 변수의 표준편차로 나눠주면 된다고 하는데.. 직접 계산할 일은 아마 없지 않을까 싶다.
- 상관계수를 보면 공분산 봤을 때와 마찬가지로 x, y가 양의 관계에 있는지 음의 관계에 있는지 볼 수 있다.
- : 음의 선형관계- : 뚜렷한 연관이 없음.
- : 양의 선형관계
- 수의 계산이므로 당연히 numerical data에 대해서만 구할 수 있는데, categorical data의 경우
Spearman correlation이라는 것을 통해 구할 수 있다고 하는데.. 우선 패스! - 파이썬에서는
df.corr()를 통해서 구할 수 있다.
- 위의 예를 이어서 들면, 결과는 이렇게 나온다.
- (해석은 공분산이랑 동일하게 하면 된다)
우리가 어떨 때 이 상관계수를 쓰게 될거냐면, 나중에 데이터 분석할 때 수많은 feature 중에서 어떤 것이 타겟과 가장 연관성이 높은지 볼 때 이 상관계수를 계산해서 확인한다!!!
소소하지만 중요한 것
orthogonality
두 벡터가 직교하는 경우를 말한다. 즉, 두 벡터의 내적이 0인 경우이다.
왜 그러냐보다는 우선 이 정도만 기억하고 넘어가도 된다고 한다.
Unit Vectors (단위 벡터)
'단위 길이'를 갖는 모든 벡터라고 하는데, 말보다는 아래 예시를 보는게 더 이해가 편했다.
- 예시)
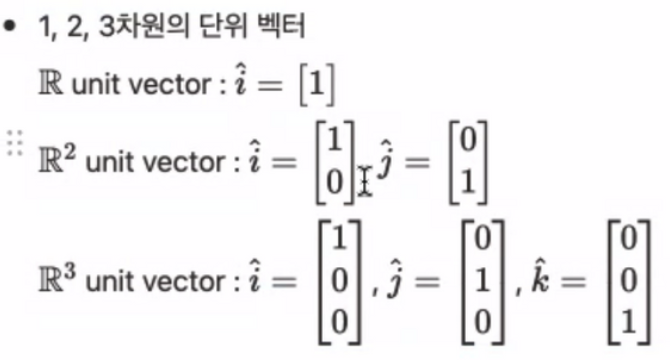
기억해야할 것은, 모든 벡터는 이 단위 벡터의 선형 조합(Linear Combination) 으로 표기할 수 있다는 것이다.
- 다른 말로 하면, 단위 벡터에 스칼라를 곱한 것이 우리가 보는 벡터다. (구성 요소가 다 1이니까 거기에 스칼라 곱하면..!)
Span
한국말로 생성이라고 번역되는 것 같은데, 그 말이 더 헷갈리니 그냥 span으로 기억하자.
먼저 span의 정의는 아래와 같다.
- 두 개 이상의 벡터의 조합(합이나 차와 같은)으로 만들 수 있는 모든 가능한 벡터의 집합.
이건 실례를 보는게 더 기억하기 쉬울거다.
- 선형관계에 있는 벡터
- 만약 두 벡터가 같은 선상에 있는 경우, 이 벡터들은 선형 관계에 있다고 말한다. (선형 종속이라고도 한다)
- 이 벡터를 아무리 조합해봤자 이 선 외부에 새로운 벡터를 생성할 수는 없다.
- 그러면 이때의 span은 직선이다~라고 말하면 된다.
- 선형관계가 없는 벡터
- 같은 선상에 있지 않은 두 벡터는 선형적으로 독립되어 있다고 말한다. (선형 독립이라고도 한다)
- 이 경우 주어진 공간 전부에 대해 두 벡터의 조합이 나타난다.
- 이럴 때는 이 두 벡터의 span은 평면이다~ 라고 말하면 된다.
이렇게 글로만 보면 나중에 헷갈릴 수 있다. 그렇다면 이 영상을 보자.
파이썬으로는 rank를 구하고 그걸 말로 표현하면 되니, 예시는 아래 rank에 달아두겠다.
Basis
Basis는 정확히 span의 역개념이다.
정확한 정의는 아래와 같다.
- 벡터 공간 V의 Basis는, V라는 공간을 채울 수 있는 선형관계에 있지 않은 벡터들의 모음이다.
물론 이렇게만 말하면 나중의 나는 아마 😮 이런 표정을 지을 거다.
그러니 예를 들어보자.
- 만약 두 벡터의 span이 평면이라고 하면, 그 평면을 만드는 두 벡터를 basis라고 한다.
BAAM!
근데 이 Basis를 자주 쓰게 될지는 모르겠다.
Rank
자, 오늘의 경험상 span이랑 같이 자주 말하는 것 같은 Rank다.
등수 뭐 그런거 아니고 쉽게 말해 차원이라고 생각하면 된다.
정확한 정의는 다음과 같다.
- 주어진 매트릭스(벡터가 2개 이상)에 대해서 매트릭스의 행 혹은 열을 이루고 있는 벡터들로 만들 수 있는 공간의 차원이다.
- (참고로 rank를 볼 때 행을 기준으로 해야하냐, 열을 기준으로 해야하냐 고민할 필요는 없다. 둘이 항상 같기 때문!)
이 rank를 생각할 때 중요한 것은 만약 벡터 간에 선형관계가 있는지를 아는 것이다.
- 만약 3개의 벡터가 있는데, 그 중 2개가 선형관계(선형종속)이라면? span은 3차원이 아닌 평면이 되고, rank도 3이 아닌 2가 된다.
만약 우리가 어떤 데이터를 보고 그것의 퀄리티를 판단할 때, 선형종속인 벡터들처럼 스케일만 다른 데이터가 있다면, 아~ 이 데이터는 좀 구리네?라고 생각할 수도 있다고 한다.
- 그렇게 판단이 되면, 데이터를 재수집하거나 혹은 분석방법을 바꾼다거나 이런 의사결정을 도와주게 된다.
참고로 이 rank는 파이썬에서 np.linalg.matirx_rank() 함수를 통해 쉽게 구할 수 있다.
예시)
다음 벡터들의 span은 뭐고 이게 의미하는 바는 무엇인가?
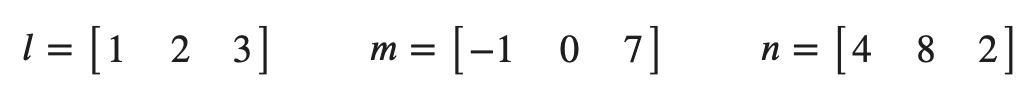
matrix = np.array([[1,2,3], [-1, 0,7], [4,8,2]])
# 다음 함수를 이용해 선형독립인 행, 열의 개수를 바로 파악할 수 있다.
res = np.linalg.matrix_rank(matrix)
print(res7)
# res7 = 3이 나오므로 위 벡터들의 span은 3차원이라고 할 수 있다. 모든 벡터는 선형독립이다.rank가 3이니 span은 3차원이다~
Linear projections
은 개념을 간단히 보았는데, 실습은 아직 해보지 못했다.
예를 들어, 벡터 w를 벡터 v로 투영시키는 것이 이 Linear projections인데,
데이터 분석시 우리에게의 이점은 정말 많은 feature들이 있을 때, 의미가 작은 피쳐들은 제거하면서(물론 loss는 좀 있겠지만) 원래 데이터가 전달하고자 하는 인사이트를 잘 파악할 수 있도록 하는, 차원 축소의 근본이 되는 개념이라고 생각하면 된다고 한다.
잊지 말자. 선형대수는 나를 도와주기 위해 있는거다 🥺
