[알고리즘] 세그먼트 트리 Segment Tree

cup-wan·2025년 8월 3일
Segment Tree세그먼트 트리알고리즘
3

Algorithm

목록 보기
4/5

이번에도 GPT한테 썸네일을 부탁했는데 이분탐색과는 다르게 4+2=9가 되는 아쉬운 모습을 보여주네요. 이미지 생성은 여전히 어려운 과제인가봐요...👽

개발을 하면서 주식 시장에서 특정 기간의 거래량 합계를 구하기, 게임 속 캐릭터의 체력이나 경험치 등 누적되는 값을 관리해야 하는 이벤트 등 데이터의 특정 구간을 다루는 일은 생각보다 자주 있습니다.

이를 쉽게 구하는 방법은 단순 for문 사용입니다. 하지만 매번 N번을 M명의 사용자에게 시도해야한다면 당연히 성능이 좋지 않습니다. 이를 해결하기 위해 세그먼트 트리를 사용할 수 있습니다.

세그먼트 트리는 구간(Segment)에 대한 정보를 트리(Tree)에 저장하여, 특정 구간의 합이나 최댓값 등을 매우 빠르게 찾아내는 자료구조

이전에 작성한 펜윅 트리보다 포괄적으로 사용되기 때문에 세그먼트 트리 먼저 작성해야 했지만... 지금이라도 포스팅해보겠습니다.

기본 구조

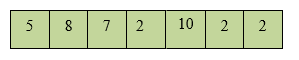
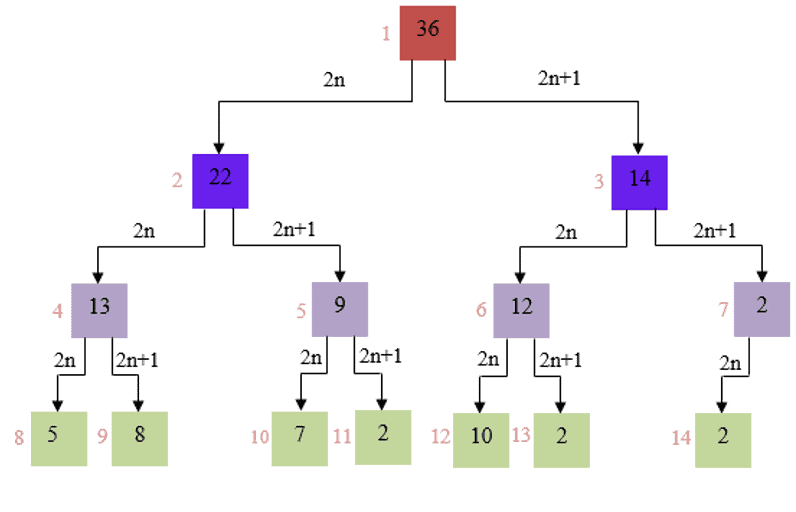
세그먼트 트리는 개념적으로는 트리지만 실제 구현할 때는 배열을 사용합니다. 위 이미지는 세그먼트 트리가 배열에 어떻게 저장되는지를 보여줍니다.

트리 구조

  • 루트 노드 (1번)은 배열 전체의 구간과 그 합(36)을 담당합니다.
  • 부모 노드는 자신의 구간을 절반으로 나누어 두 자식 노드에게 물려줍니다. (분할 정복)
  • 이 과정은 더 이상 나눌 수 없는, 즉 원소 1개짜리 구간에 도달할 때 까지 반복됩니다. 트리의 가장 아래에 있는 노드 (리프 노드)들이 원본 배열의 각 원소가 됩니다.

배열 구조

  • 이미지의 보라색 배열이 이 트리 구조를 1차원 배열에 옮겨 담은 실제 구현 모습입니다.
  • 트리를 배열로 표현하기 위해 인덱스 규칙을 사용합니다.
    • 부모 노드가 배열 n번 인덱스에 있다면
    • 왼쪽 자식은 2 * n번 인덱스
    • 오른쪽 자식은 2 * n + 1번 인덱스

이렇게 배열로 표현하여 특정 노드의 부모나 자식을 복잡한 연결 과정 없이 인덱스 계산으로 빠르게 찾아가게 됩니다.

핵심 동작 원리 및 구현

트리 생성 (init)

우선, 주어진 배열을 바탕으로 각 구간의 합을 미리 계산해 세그먼트 트리 배열에 저장해야 합니다. 이 과정은 재귀를 이용해 구현합니다.

💡 Logic
1. 탐색은 루트 노드 (인덱스 1)에서 시작하며, 루트는 전체 배열 구간 (0~N-1)을 담당
2. 현재 노드가 담당하는 구간을 자식들에게 절반씩 나눠주며 재귀적으로 더 깊이 탐색 (분할)
3. 더 이상 나눌 수 없는, 즉 원소가 1개인 리프 노드에 도달하면, 해당 배열의 원소를 트리 노드에 저장
4. 재귀 호출이 끝나고 돌아오면서, 자식 노드들의 값을 합쳐 현재 노드의 값을 계산 (정복)

import java.util.Arrays;

public class SegmentTree {

    long[] arr;  // 원본 배열
    long[] tree; // 세그먼트 트리 배열

    public SegmentTree(long[] arr) {
        this.arr = arr;
        this.tree = new long[arr.length * 4];
        
        // 트리 생성(초기화) 메서드 호출
        // 시작: 루트 노드(인덱스 1), 담당 구간: 배열 전체(0 ~ N-1)
        init(0, arr.length - 1, 1);
    }

    /**
     * 세그먼트 트리 초기화 메서드
     * @param start 현재 노드가 담당하는 원본 배열의 시작 인덱스
     * @param end   현재 노드가 담당하는 원본 배열의 끝 인덱스
     * @param node  현재 세그먼트 트리 노드의 인덱스
     * @return      생성된 노드의 값 (자식에게 값을 물려주기 위함)
     */
    private long init(int start, int end, int node) {
        // 1. 리프 노드일 경우 (더 이상 분할할 수 없을 때)
        if (start == end) {
            // 원본 배열의 값을 트리 노드에 저장
            return this.tree[node] = this.arr[start];
        }

        // 2. 내부 노드일 경우 (분할이 가능할 때)
        int mid = (start + end) / 2; // 구간을 나눌 중간 지점

        // 왼쪽 자식(node*2)과 오른쪽 자식(node*2+1)을 재귀적으로 호출
        long leftChildValue = init(start, mid, node * 2);
        long rightChildValue = init(mid + 1, end, node * 2 + 1);
        
        // 3. 자식들의 합을 현재 노드에 저장 (정복)
        return this.tree[node] = leftChildValue + rightChildValue;
    }
}

  • tree 배열 크기를 4*(원본 배열 크기)로 상정한 이유

    • 세그먼트 트리는 자식에게 절반씩 나눠주기 때문에 완전 이진 트리형태로 구현
    • 트리의 높이를 h라 할 때, 필요 노드 개수는 N에 따라 다름
    • n이 2의 거듭제곱인 경우 : h = log2(n) + 1, 노드 수 = 2 * (n-1)
    • n이 2의 거듭제곱이 아닌 경우 : 완전 이진 트리 형태 유지를 위해 n 보다 큰 가장 가까운 2의 거듭제곱 까지 필요
      • n = 6이라면 2^2 < n < 2^3 이기 때문에 8이 필요
      • 이를 방지하기 위해 4*n으로 넉넉하게 설정

  • 나머지는 모두 기존 logic을 따라가는 코드

구간 합 구하기 (query)

초기화가 완료된 세그먼트 트리를 이용해 특정 구간의 합을 구하는 메서드 입니다.

💡 Logic
1. (No Overlap) 현재 노드 구간이 내가 찾는 구간과 전혀 겹치지 않으면, 합계에 영향을 주지 않는 값(0)을 반환합니다.
2. (Full Overlap) 현재 노드 구간이 내가 찾는 구간 안에 완전히 포함되면, 이 노드에 저장된 값을 바로 반환합니다. 더 깊이 탐색할 필요가 없습니다.
3. (Partial Overlap) 일부만 겹치면, 왼쪽 자식과 오른쪽 자식에게 각각 탐색을 위임하고, 그 결과들을 더해서 반환합니다.

public class SegmentTree {

	// ....

    /**
     * 구간 합을 구하는 메서드
     * @param left  구하고자 하는 구간의 시작 인덱스
     * @param right 구하고자 하는 구간의 끝 인덱스
     * @return      구간의 합
     */
    public long query(int left, int right) {
        // 내부 재귀 함수를 호출하여 결과를 반환
        return query(0, arr.length - 1, 1, left, right);
    }

    private long query(int start, int end, int node, int left, int right) {
        // Case 1: No Overlap (찾는 구간과 현재 노드 구간이 겹치지 않음)
        if (left > end || right < start) {
            return 0;
        }

        // Case 2: Full Overlap (찾는 구간이 현재 노드 구간을 완전히 포함)
        if (left <= start && end <= right) {
            return this.tree[node];
        }

        // Case 3: Partial Overlap (일부만 겹침)
        // 왼쪽 자식과 오른쪽 자식 모두 확인 후 그 합을 반환
        int mid = (start + end) / 2;
        long leftSum = query(start, mid, node * 2, left, right);
        long rightSum = query(mid + 1, end, node * 2 + 1, left, right);
        return leftSum + rightSum;
    }
}
  • if (left > end || right < start) : 찾으려는 구간 [left, right] 가 현재 노드가 담당하는 [start, end]를 완전히 벗어난 경우. 더 이상 볼 필요가 없기에 0을 반환
  • if (left <= start && end <= right) : 현재 노드 구간 [start, end]가 찾으려는 구간 [left, right] 안에 딱 들어오는 경우. 이 노드 (tree[node])에는 해당 구간의 합이 이미 계산되어 있기에 그 값을 바로 사용.
  • return leftSum + right Sum : 겹치지만 완전히 들어오진 않는 경우. 어쩔 수 없이 왼쪽 자식과 오른쪽 자식 모두에게 겹치는 부분이 있는지 확인 후 합쳐서 return

값 변경하기 (update)

배열의 특정 원소 값이 바뀌면 그 값을 포함하는 모든 구간의 합이 영향을 받습니다. 해당 원소를 포함하는 리프 노드부터 루트 노드까지의 경로에 있는 모든 노드 값을 갱신해야 합니다.

💡 Logic
1. 값을 변경할 원소의 인덱스와 값의 차이(diff = newValue - oldValue)를 계산
2. 루트부터 시작해 인덱스를 포함하는 노드들을 따라 리프 노드까지 탐색
3. 탐색 경로에 있는 모든 노드들의 값에 diff만큼 더함. 자식들의 값을 다시 계산할 필요 없이, 차이값만 반영 (이 반영을 늦추는 방식이 lazy propagation)

/**
* 특정 원소의 값을 변경하는 외부 호출용 메서드
* @param index     값을 변경할 원소의 인덱스
* @param newValue  새로운 값
*/
public void update(int index, long newValue) {
   long diff = newValue - this.arr[index]; // 기존 값과 새로운 값의 차이
   this.arr[index] = newValue; // 원본 배열의 값도 갱신해준다.
   update(0, arr.length - 1, 1, index, diff);
}

private void update(int start, int end, int node, int index, long diff) {
    // Case 1: 변경할 index가 현재 노드 구간과 관련 없는 경우
    if (index < start || index > end) {
       return;
    }

    // Case 2: 현재 노드 구간이 변경할 index를 포함하는 경우
    // -> 현재 노드 값에 차이(diff)를 반영한다.
    this.tree[node] += diff;

    // 리프 노드가 아니라면, 자식 노드도 재귀적으로 찾아 내려간다.
    if (start != end) {
        int mid = (start + end) / 2;
        update(start, mid, node * 2, index, diff);
        update(mid + 1, end, node * 2 + 1, index, diff);
    }
}
  • if (index < start || index > end) : 변경하려는 인덱스가 현재 노드가 담당하는 구간에 포함되지 않으면 이 노드와 그 자식들은 값의 변화와 아무 관련 X. 더 깊이 탐색하지 않고 즉시 return
  • if (start != end) : 현재 노드가 리프 노드가 아닌 경우에만 재귀 호출을 계속해 경로상의 모든 노드 갱신

[전체 코드]

import java.util.Arrays;

public class SegmentTree {

    long[] arr;
    long[] tree;

    public SegmentTree(long[] arr) {
        this.arr = arr;
        this.tree = new long[arr.length * 4];
        init(0, arr.length - 1, 1);
    }

    private long init(int start, int end, int node) {
        if (start == end) {
            return this.tree[node] = this.arr[start];
        }
        int mid = (start + end) / 2;
        return this.tree[node] = init(start, mid, node * 2) + init(mid + 1, end, node * 2 + 1);
    }

    public long query(int left, int right) {
        return query(0, arr.length - 1, 1, left, right);
    }

    private long query(int start, int end, int node, int left, int right) {
        if (left > end || right < start) {
            return 0;
        }
        if (left <= start && end <= right) {
            return this.tree[node];
        }
        int mid = (start + end) / 2;
        return query(start, mid, node * 2, left, right) + query(mid + 1, end, node * 2 + 1, left, right);
    }
    
    public void update(int index, long newValue) {
        long diff = newValue - this.arr[index];
        this.arr[index] = newValue;
        update(0, arr.length - 1, 1, index, diff);
    }

    private void update(int start, int end, int node, int index, long diff) {
        if (index < start || index > end) {
            return;
        }
        this.tree[node] += diff;
        if (start != end) {
            int mid = (start + end) / 2;
            update(start, mid, node * 2, index, diff);
            update(mid + 1, end, node * 2 + 1, index, diff);
        }
    }

시간 복잡도

세그먼트 트리가 빠른 이유는 인덱스 규칙을 활용한 트리 개념 활용에 있습니다.

  • 트리 생성 (init) 시 모든 노드를 한 번씩 방문하기 때문에 시간 복잡도가 O(N) 입니다.
  • 구간 합 & 값 변경 (query & update) 는 모두 트리의 높이에 비례하는 시간이 걸립니다 (리프 to 루트). 트리의 높이는 약 logN 이므로 두 연산 모두 O(logN)이 걸립니다.
profile
cup-wan
아무것도 안해서 유죄 판결 받음
이전 포스트

[알고리즘] 펜윅 트리 Fenwick Tree

다음 포스트

[알고리즘] 표 편집

0개의 댓글