카카오 공채 문제가 아주 재밌습니다. 그 중 문제가 정말 좋다! 배운 것이 많다! 싶은 것만 골라서 기록을 남겨두려 합니다.
그 첫 문제로 표 편집 문제를 소개합니다.
이번 썸네일은 제미나이가 수고해줬습니다. 지피티랑 비슷한 수준;인 것 같아요.

문제
업무용 소프트웨어를 개발하는 니니즈웍스의 인턴인 앙몬드는 명령어 기반으로 표의 행을 선택, 삭제, 복구하는 프로그램을 작성하는 과제를 맡았습니다. 세부 요구 사항은 다음과 같습니다
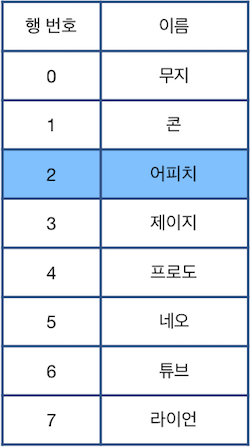
위 그림에서 파란색으로 칠해진 칸은 현재 선택된 행을 나타냅니다. 단, 한 번에 한 행만 선택할 수 있으며, 표의 범위(0행 ~ 마지막 행)를 벗어날 수 없습니다. 이때, 다음과 같은 명령어를 이용하여 표를 편집합니다.
"U X": 현재 선택된 행에서 X칸 위에 있는 행을 선택합니다.
"D X": 현재 선택된 행에서 X칸 아래에 있는 행을 선택합니다.
"C" : 현재 선택된 행을 삭제한 후, 바로 아래 행을 선택합니다. 단, 삭제된 행이 가장 마지막 행인 경우 바로 윗 행을 선택합니다.
"Z" : 가장 최근에 삭제된 행을 원래대로 복구합니다. 단, 현재 선택된 행은 바뀌지 않습니다.
예를 들어 위 표에서 "D 2"를 수행할 경우 아래 그림의 왼쪽처럼 4행이 선택되며, "C"를 수행하면 선택된 행을 삭제하고, 바로 아래 행이었던 "네오"가 적힌 행을 선택합니다(4행이 삭제되면서 아래 있던 행들이 하나씩 밀려 올라오고, 수정된 표에서 다시 4행을 선택하는 것과 동일합니다).
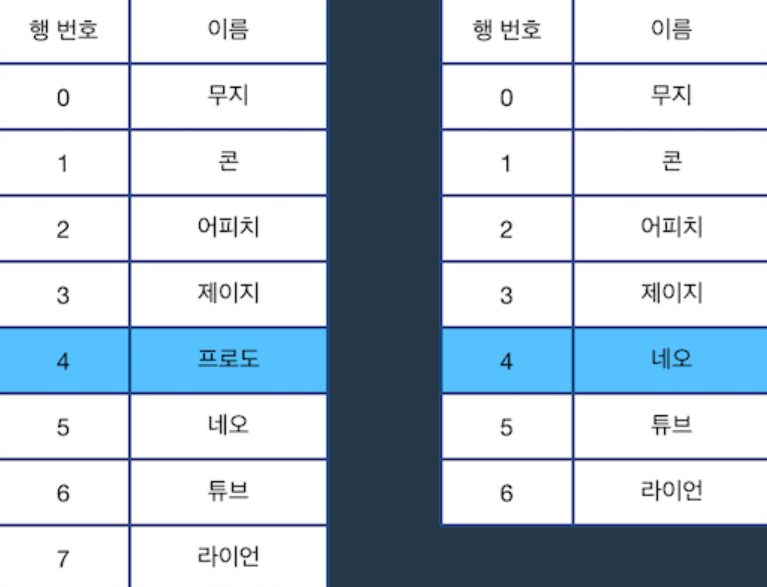
다음으로 "U 3"을 수행한 다음 "C"를 수행한 후의 표 상태는 아래 그림과 같습니다.
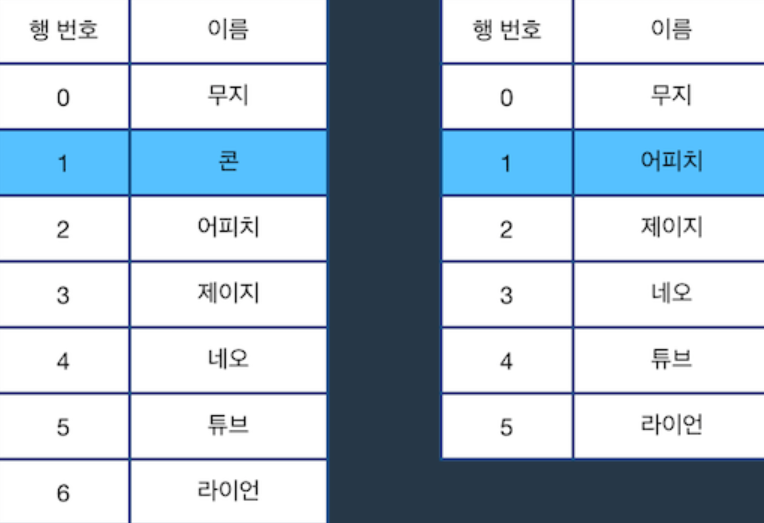
다음으로 "D 4"를 수행한 다음 "C"를 수행한 후의 표 상태는 아래 그림과 같습니다. 5행이 표의 마지막 행 이므로, 이 경우 바로 윗 행을 선택하는 점에 주의합니다.
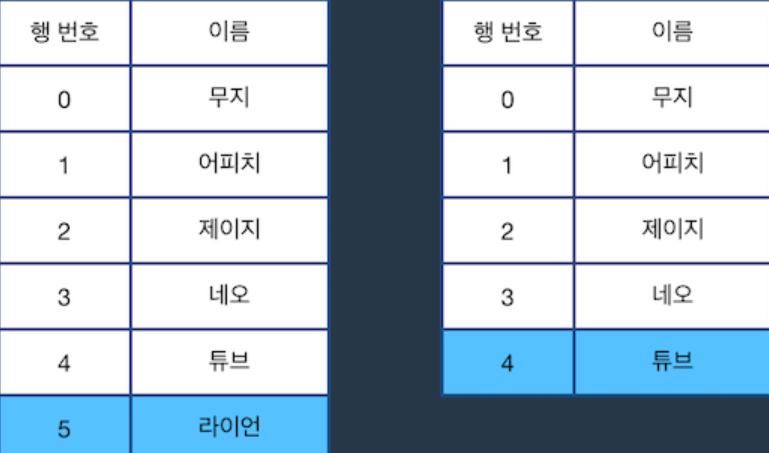
다음으로 "U 2"를 수행하면 현재 선택된 행은 2행이 됩니다.
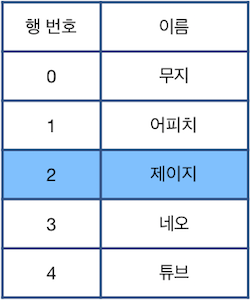
위 상태에서 "Z"를 수행할 경우 가장 최근에 제거된 "라이언"이 적힌 행이 원래대로 복구됩니다.
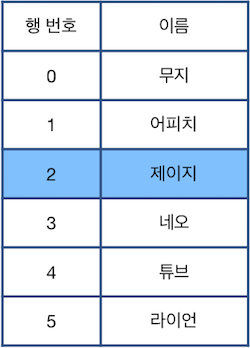
다시한번 "Z"를 수행하면 그 다음으로 최근에 제거된 "콘"이 적힌 행이 원래대로 복구됩니다. 이때, 현재 선택된 행은 바뀌지 않는 점에 주의하세요.
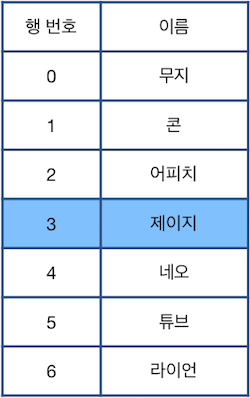
이때, 최종 표의 상태와 처음 주어진 표의 상태를 비교하여 삭제되지 않은 행은 "O", 삭제된 행은 "X"로 표시하면 다음과 같습니다.
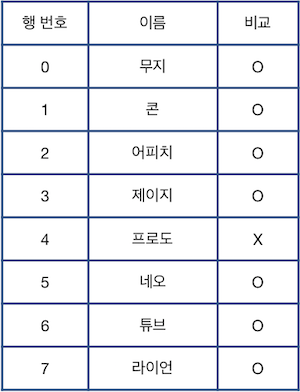
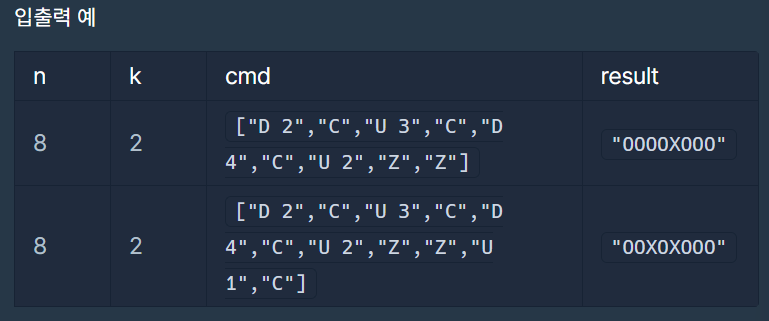
처음 표의 행 개수를 나타내는 정수 n, 처음에 선택된 행의 위치를 나타내는 정수 k, 수행한 명령어들이 담긴 문자열 배열 cmd가 매개변수로 주어질 때, 모든 명령어를 수행한 후 표의 상태와 처음 주어진 표의 상태를 비교하여 삭제되지 않은 행은 O, 삭제된 행은 X로 표시하여 문자열 형태로 return 하도록 solution 함수를 완성해주세요.
제한사항
- 5 ≤
n≤ 1,000,000 - 0 ≤
k<n - 1 ≤
cmd의 원소 개수 ≤ 200,000cmd의 각 원소는"U X","D X","C","Z"중 하나입니다.- X는 1 이상 300,000 이하인 자연수이며 0으로 시작하지 않습니다.
- X가 나타내는 자연수에 ',' 는 주어지지 않습니다. 예를 들어 123,456의 경우 123456으로 주어집니다.
cmd에 등장하는 모든 X들의 값을 합친 결과가 1,000,000 이하인 경우만 입력으로 주어집니다.- 표의 모든 행을 제거하여, 행이 하나도 남지 않는 경우는 입력으로 주어지지 않습니다.
- 본문에서 각 행이 제거되고 복구되는 과정을 보다 자연스럽게 보이기 위해
"이름"열을 사용하였으나,"이름"열의 내용이 실제 문제를 푸는 과정에 필요하지는 않습니다."이름"열에는 서로 다른 이름들이 중복없이 채워져 있다고 가정하고 문제를 해결해 주세요.
- 표의 범위를 벗어나는 이동은 입력으로 주어지지 않습니다.
- 원래대로 복구할 행이 없을 때(즉, 삭제된 행이 없을 때) "Z"가 명령어로 주어지는 경우는 없습니다.
- 정답은 표의 0행부터 n - 1행까지에 해당되는 O, X를 순서대로 이어붙인 문자열 형태로 return 해주세요.
정확성 테스트 케이스 제한 사항
- 5 ≤
n≤ 1,000 - 1 ≤
cmd의 원소 개수 ≤ 1,000
효율성 테스트 케이스 제한 사항
- 주어진 조건 외 추가 제한사항 없습니다.
아이디어 + 풀이
1. 스택
그림이 너무 스택을 쓰고싶게 나와서 스택을 사용할까 했습니다. 구현이 굉장히 쉽고 n과 cmd가 1000 이하이기 때문에 시간복잡도도 O(n*cmd) 라 괜찮습니다.
라고 생각했습니다.
import java.util.*;
class Solution {
public String solution(int n, int k, String[] cmd) {
boolean[] alive = new boolean[n];
Arrays.fill(alive, true);
Deque<Integer> stack = new ArrayDeque<>();
int cur = k;
for (String s : cmd) {
char op = s.charAt(0);
if (op == 'U' || op == 'D') {
int x = Integer.parseInt(s.substring(2));
if (op == 'U') {
while (x-- > 0) {
int p = cur - 1;
while (p >= 0 && !alive[p]) p--;
if (p >= 0) cur = p;
}
} else {
while (x-- > 0) {
int q = cur + 1;
while (q < n && !alive[q]) q++;
if (q < n) cur = q;
}
}
} else if (op == 'C') {
stack.push(cur);
alive[cur] = false;
int q = cur + 1;
while (q < n && !alive[q]) q++;
if (q < n) {
cur = q;
} else {
int p = cur - 1;
while (p >= 0 && !alive[p]) p--;
cur = p;
}
} else { // 'Z'
int rec = stack.pop();
alive[rec] = true;
}
}
StringBuilder sb = new StringBuilder();
for (int i = 0; i < n; i++) sb.append(alive[i] ? 'O' : 'X');
return sb.toString();
}
}
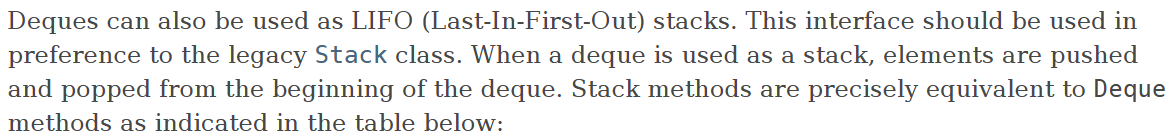

- JDK 공식 문서에서 LIFO 자료구조로
Stack클래스 보다Deque사용 권장 ArrayDeque가Stack보다 빠를 가능성이 있다.
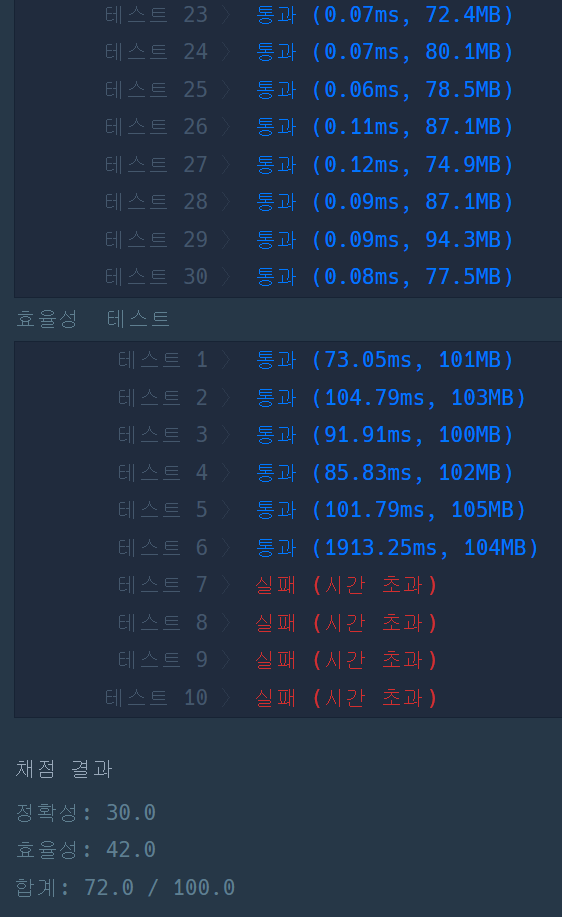
효율성 테스트에서 박살이 났는데 왜 그런걸까요?
U x/D x를 처리할 때마다alive[p]가false인 구간을 while로 뛰어넘는 선형 스캔 ➡️ 최악O(n*이동횟수)- 이동횟수 = 죽은 구간 길이 X 그 구간을 건너뛴 횟수 : 각 이동마다 죽은 칸을 건너뛰는 비용이 추가됨
2. 펜윅 트리 (BIT)
최근..?에 작성한 펜윅 트리가 생각나서 펜윅트리로 풀어봤습니다. 핵심 아이디어는 다음과 같습니다.
- 살아있는 행을 0/1로 표현
alive[i] = 1(살) / 0(죽)을 펜윅 트리에 저장
sum(i)=1...i구간에 살아있는 행의 개수 = i번째 인덱스의 순위- 커서가 보고 있는 인덱스
cur의 현재 순위는r = sum(cur)
- 커서가 보고 있는 인덱스
D x-> 순위를r+x로,U x-> 순위를r-x로- 삭제/복구는 해당 위치의 값을 +1 or -1 업데이트로 반영
kth(k)에서k가 1~tot 범위로 들어오는지 확인 (삭제 이후 tot=0이 되지 않는다는 보장)
import java.util.*;
class Solution {
static class BIT {
int n;
int[] bit;
BIT(int n){
this.n=n;
bit = new int[n+1];
}
void add(int i,int d){
for(; i<=n; i+=i&-i) bit[i]+=d;
}
int sum(int i){
int s=0;
for(; i>0; i-=i&-i) s+=bit[i];
return s;
}
int kth(int k){
int idx=0,mask=1;
while((mask<<1)<=n) mask<<=1;
for(int d=mask; d!=0; d>>=1){
int nxt=idx+d;
if(nxt<=n && bit[nxt]<k){
k-=bit[nxt];
idx=nxt;
}
}
return idx+1;
}
}
public String solution(int n, int k, String[] cmd) {
BIT ft = new BIT(n);
boolean[] alive = new boolean[n];
Arrays.fill(alive,true);
for(int i = 1; i <= n; i++) ft.add(i,1);
Deque<Integer> st=new ArrayDeque<>();
int cur = k+1;
for(String s:cmd){
char op=s.charAt(0);
if(op == 'U' || op == 'D'){
int x = Integer.parseInt(s.substring(2));
int r = ft.sum(cur) + (op=='D'?x:-x);
cur = ft.kth(r);
}else if(op == 'C'){
int r = ft.sum(cur);
st.push(cur);
ft.add(cur,-1);
alive[cur-1]=false;
int tot = ft.sum(n);
cur=(r<=tot)?ft.kth(r):ft.kth(tot);
}else{
int rec = st.pop();
ft.add(rec,1);
alive[rec-1]=true;
}
}
StringBuilder sb=new StringBuilder();
for(int i=0;i<n;i++) sb.append(alive[i]?'O':'X');
return sb.toString();
}
}
- 장점
- 멋있다! 펜윅 트리 실전 사용 성공이다!
- 살아있는 개수(순위) 기준이라 스택의 문제점이었던 k번째 살아있는 원소의 실제 위치를
kth(k)로 한번에 접근 가능해졌다!
- 단점
- 구현이 어렵다
- 이중연결리스트보다 느림
U x,D x에서 x 값이 크면 BIT가 유리 (연결 리스트 : O(x), 펜윅트리 : O(log n)
3. 연결 리스트
2번 방법이 멋있지만 구현이 솔직히 너무 어렵고 다른 문제에서 구현하라면 자신이 없습니다.
결국 중간 다리 건너뛰는 것이 중요한 문제라 생각해서 연결 리스트가 생각났습니다.
prev[i],next[i]: i의 이웃 포인터, 삭제 시 이웃끼리 포인터 연결stack(ArrayDeque):{row, prev, next}push ➡️ 복구 시 포인터 원상 복구- 이동 : 포인터만 x번 이동 (
O(x), 죽은 구간 스캔 사라짐)
import java.util.*;
class Solution {
public String solution(int n, int k, String[] cmd) {
int[] prev = new int[n];
int[] next = new int[n];
boolean[] alive = new boolean[n];
Arrays.fill(alive, true);
// prev, next 값이 -1인 인덱스가 양 끝
for (int i = 0; i < n; i++) {
prev[i] = i - 1;
next[i] = i + 1;
}
next[n - 1] = -1;
// 삭제된 거 복구용
Deque<int[]> stack = new ArrayDeque<>();
int cur = k;
for (String c : cmd) {
char op = c.charAt(0);
if (op == 'U' || op == 'D') { // 위, 아래
int x = Integer.parseInt(c.substring(2));
if (op == 'U') while (x-- > 0) cur = prev[cur];
else while (x-- > 0) cur = next[cur];
} else if (op == 'C') { // 삭제
stack.push(new int[]{cur, prev[cur], next[cur]});
alive[cur] = false;
if (prev[cur] != -1) next[prev[cur]] = next[cur];
if (next[cur] != -1) prev[next[cur]] = prev[cur];
cur = (next[cur] != -1) ? next[cur] : prev[cur];
} else { // 복구
int[] rec = stack.pop();
int row = rec[0], p = rec[1], q = rec[2];
alive[row] = true;
if (p != -1) next[p] = row;
if (q != -1) prev[q] = row;
prev[row] = p;
next[row] = q;
}
}
StringBuilder sb = new StringBuilder();
for (int i = 0; i < n; i++) sb.append(alive[i] ? 'O' : 'X');
return sb.toString();
}
}
- 장점
- 정석 풀이? 같습니다
- 구현이 매우 쉬움
- 가장 빠름
- 삭제/복구 O(1), 이동 O(x)
- 단점
- 펜윅트리 대비 메모리가 아~~주 근소하게 더 필요
제미나이가 만들어준 썸네일 후보로 마무리하겠습니다. Easy, right? 개열받음