
GPT가 만들어 준 썸네일인데 텍스트도 잘만들어주는 것이 너무..너무 무섭습니다.. 그만 발전해....
이분 탐색이 항상 어려워서 코딩테스트 난이도 정도의 이분 탐색에 대한 글입니다. 엄청 어려운 이분 탐색 + a 내용은 없습니다.
주로 핵심 개념이라 생각하는 while문의 조건 선택, lower bound + upper bound을 중점적으로 작성했습니다.
개념
이분 탐색은 정렬된 데이터에서 구간을 절반씩 나눠가며 좁혀가는 방식으로 원하는 값을 빠르게 찾는 알고리즘
시간 복잡도 :
1 ~ 100 사이의 숫자를 맞추는 Up&Down 게임을 한다 했을 때 어떻게 찾으시나요?
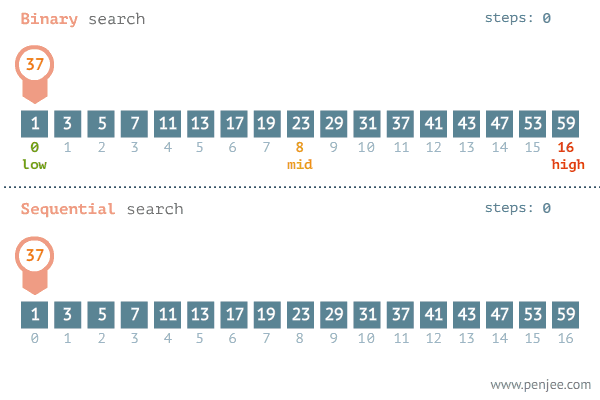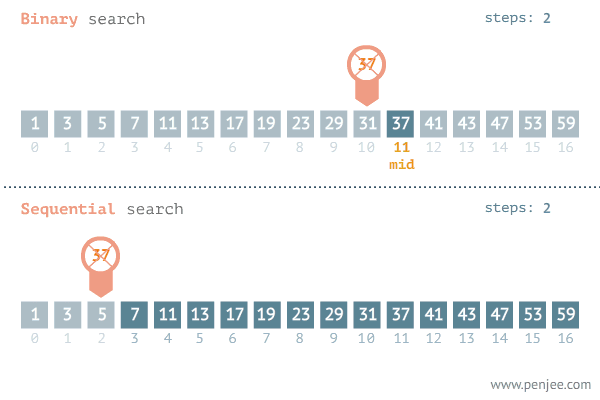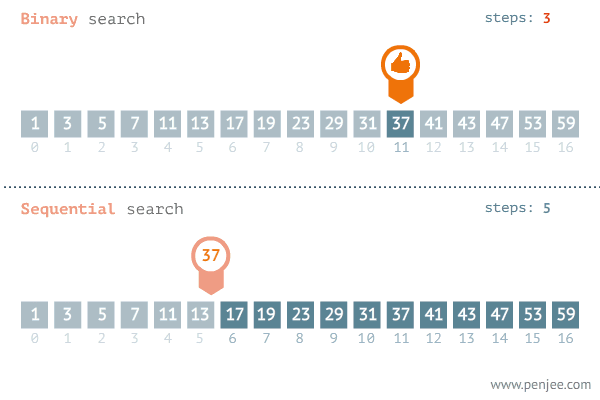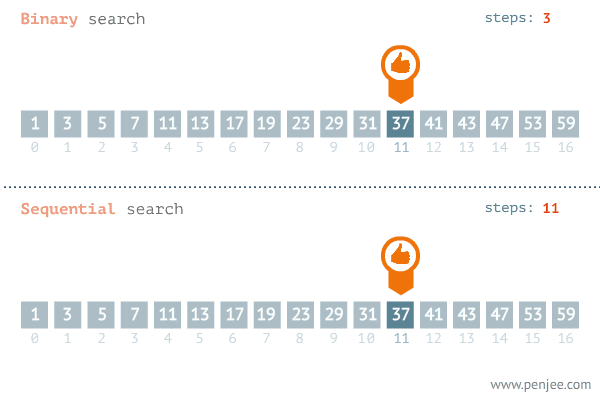
가장 단순한 방법은 선형 탐색입니다. 주어진 데이터의 처음부터 끝까지 순차적으로 돌면서 원하는 값이 있는지 확인하는 방법으로 정렬이 필요없지만 최악의 경우 모든 데이터를 다 확인해봐야하기 때문에 의 시간 복잡도를 갖게 됩니다.
하지만 실제로 사람들은 처음으로 50을 외칠 것 입니다. 범위를 반씩 줄여가며 탐색하는 이분 탐색이 더 빠르다는 것을 체감하고 있기 때문입니다. 100이 아닌 1,000,000 개의 데이터가 있다고 하면 더 체감이 됩니다. 선형 탐색은 100만개의 데이터 모두 시도해봐야하지만 이분 탐색은 이기 때문에 최대 20번에 찾을 수 있습니다.
이분 탐색은 다음과 같은 흐름으로 동작합니다.
1. 탐색 구간 초기화
left = 0, right = len(arr) - 1
2. 중간값 (mid) 계산)
mid = (left + right) / 2
3. 값 비교 및 범위 조정
arr[mid] == target : 답
arr[mid] < target : 왼쪽은 제외 ➡️ left = mid + 1
arr[mid] > target : 오른쪽 제외 ➡️ right = mid - 1
위 과정을 java 코드로 옮기면
public class BinarySearch {
public static int binarySearch(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = (left + right) / 2;
if (arr[mid] == target) {
return mid;
} else if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}
}lower_bound, upper_bound
이분 탐색의 구현 자체는 단순합니다. 하지만 특정 값을 찾을 때만 단순 구현으로 ps가 가능합니다. 다음과 같은 경우엔 lower_bound, upper_bound 개념이 필요합니다.
- 어떤 값이 몇 개 있는지 세기
- 어떤 값 이상인 첫 위치 찾기
- 어떤 값보다 큰 값이 처음 나오는 지점 찾기
- 데이터를 정렬 상태로 유지하면서 적절한 삽입 위치 찾기
이 상한선, 하한선 내용이 굉장히 헷갈립니다. 백준에 잘 정리된 글이 있으니 같이 읽어보셔도 좋을 것 같아요.
개념부터 정리하고 가겠습니다.
| 함수 이름 | 의미 | 조건 |
|---|---|---|
lower_bound | target 이상(>=)이 처음 나타나는 인덱스 | arr[i] >= target |
upper_bound | target 초과(>)가 처음 나타나는 인덱스 | arr[i] > target |
두 함수 모두 "해당 조건을 만족하는 첫 번째 위치" 를 찾습니다.
이분 탐색을 값 자체를 찾기 위한 목적이 아닌, 특정 조건을 만족하는 최소 인덱스를 찾기 위해 사용합니다.
left: 항상 유효 후보군right: 항상 무효 후보군left < right: 조건을 만족하는 가장 왼쪽 경계로 수렴
[lower_bound 구현]
// arr[i] >= target인 첫 번째 위치를 반환
public static int lowerBound(int[] arr, int target) {
int left = 0;
int right = arr.length;
while (left < right) {
int mid = left + (right - left) / 2;
if (arr[mid] < target) {
// target보다 작은 값은 제외해도 됨
left = mid + 1;
} else {
// target 이상이면 범위에 포함될 수 있음 → 계속 왼쪽으로 이동
right = mid;
}
}
return left; // !!!!left가 항상 유효 후보군!!!!
}[upper_bound 구현]
// arr[i] > target인 첫 번째 위치를 반환
public static int upperBound(int[] arr, int target) {
int left = 0;
int right = arr.length;
while (left < right) {
int mid = left + (right - left) / 2;
if (arr[mid] <= target) {
// target 이하인 값은 후보 제외
left = mid + 1;
} else {
// target 초과 가능성 있음 → 계속 왼쪽으로 이동
right = mid;
}
}
return left;
}이분 탐색 코드에서는 while(left <= right), return mid 였는데 왜 upper_bound, lower_bound에서는 while(left < right) , return left일까요?
while 문의 종료 조건에 따라 달라지는 것이므로 개념을 확실히 알고 사용해야합니다.
while (left <= right)= 정답이 정확히 배열 안에 있을 때
public static int binarySearch(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while (left <= right) { // 등호 포함
int mid = left + (right - left) / 2;
if (arr[mid] == target) {
return mid; // 정답
} else if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1; // 정답 없음
}- 종료 조건 :
left > right➡️ 범위 다 돌아도 못 찾음 - 탐색 대상 : 정확히 일치하는 값
💡
left == right인 순간도 비교하는 경우<=사용
while(left < right)= 조건을 만족하는 최소 위치를 찾는 경우
// 조건을 만족하는 "가장 왼쪽 경계"를 찾기 위함
while (left < right) {
int mid = left + (right - left) / 2;
if (조건을 만족하는가?) {
right = mid;
} else {
left = mid + 1;
}
}
return left; // 또는 right (같음)- 종료 조건 :
left >= right➡️left = right일 때 while문 종료 left == right일 때 해당 값을 반환함- 정확한 값의 존재 여부 X, 조건을 만족하는 최초 인덱스를 찾음 (그 값이 배열의 끝일 수도 있기 때문에 left == right 까지 조사)
- lower_bound나 upper_bound는 조건을 만족하는 값이 배열에 존재하지 않아도, 그 값이 정렬을 유지하며 들어갈 수 있는 위치를 반환합니다. 예를 들어 lower_bound(arr, 10)에서 arr이 {1, 2, 5}라면 결과는 3입니다.
매개변수 탐색 (Parametric Search)
항상 이분탐색하면 같이 나와주는 매개변수 탐색입니다. 이분탐색은 하나의 값을 찾는 알고리즘이라면 매개변수 탐색은 이분탐색을 이용하여 가장 적절한 값을 찾아주는 알고리즘입니다. 예제를 통해 확실한 구분이 가능합니다.
[백준 2110] 공유기 설치
대표적인 매개 변수 탐색 문제인 공유기 설치입니다.
- 정답이 명확하지 않음 : 값을 직접 찾는 것이 아닌 ((특정 조건을 만족하는 값 중에 가장 적절한 값))을 바랍니다. 해당 문제에선 가장 적절한 값 = 최대값 입니다.
- 이분 탐색을 통해 범위를 좁혀 나갈 수 있습니다.
isValid()같이 유효성을 검사하는 함수를 사용하게 됩니다.
import java.io.*;
import java.util.*;
public class Main {
static int N, C, ans;
static int[] nums;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
C = Integer.parseInt(st.nextToken());
nums = new int[N];
for(int i = 0 ; i < N; i++) {
nums[i] = Integer.parseInt(br.readLine());
}
Arrays.sort(nums);
int left = 1, right = nums[N-1] - nums[0];
while(left <= right) {
int mid = (left + right) / 2;
if(isValid(mid)){
ans = mid;
left = mid + 1;
}else {
right = mid -1;
}
}
System.out.println(ans);
}
private static boolean isValid(int dist) {
int cnt = 1;
int last = nums[0];
for(int i = 1; i < N; i++) {
if(nums[i] - last >= dist) {
cnt ++;
last = nums[i];
}
if(cnt >= C) return true;
}
return false;
}
}활용 사례
Arrays.binarySearch()
int result = Arrays.binarySearch(int[] arr, int key)
result >= 0 : key의 인덱스
result < 0 : key가 존재 X ➡️ 삽입 위치를 반환
Java에서는 배열에서 이분 탐색을 수행할 때 직접 구현하지 않고 사용할 수 있는 표준 라이브러리를 제공합니다.

key 값을 찾으면 인덱스를 리턴하고 없으면 -Insertion point - 1값을 반환한다고 합니다.
이 값은 key를 배열에 삽입해서 정렬 상태를 유지하려할 때 어디에 삽입해야 하는지 알려주는 위치입니다.
int[] arr = {1, 3, 5, 7};
System.out.println(Arrays.binarySearch(arr, 5)); // 2 (존재)
System.out.println(Arrays.binarySearch(arr, 4)); // -3 (→ 삽입 위치 2)즉, 음수 값이면 -(result + 1)를 하면 어디에 삽입해야하는지가 나옵니다. 이렇게 복잡하게 설정한 이유는 아마 삽입 위치가 0일 경우를 고려해서라 생각합니다.
이 라이브러리의 key 값은 lower_bound 처럼 항상 최소 인덱스를 보장하지 않기 때문에 중복 요소가 있을 경우 보장된 위치가 아닙니다.
LIS
최장 증가 수열인 LIS 문제에서도 이분 탐색이 사용됩니다.
현재 숫자가 들어갈 위치를 이분 탐색으로 찾은 후 그 위치에 값을 덮어 씌우는 방식입니다.
List<Integer> lis = new ArrayList<>();
for (int num : arr) {
int pos = Collections.binarySearch(lis, num);
if (pos < 0) pos = -(pos + 1);
if (pos == lis.size()) lis.add(num);
else lis.set(pos, num);
}