[알고리즘] 최단 경로 알고리즘 선택 가이드

cup-wan·2025년 6월 15일

알고리즘

Algorithm

목록 보기

2/5

BFS

가중치가 없는 경우 선택

가중치가 0 / 1 로 이루어져 있을 때 선택

가중치가 있지만 0 / 1 이라면 다익스트라가 아닌 BFS로 풀이가 가능
다익스트라 시간 복잡도
- 이진 힙 사용 (pq) = $O(ElogV)$
- 피보나치 힙 사용 = $O( E+VlogV)$

0-1 BFS

Queue 가 아닌, Deque 을 활용

가중치가 0 이면 앞에 삽입, 1 이면 뒤에 삽입

for all v in verticces:
    dist[v] = inf
dist[start] <- 0
deque d
d.push_front(start)

while d.empty() == false:
    vertex = get front element and pop as in BFS
    for all edges e of form(vertex, u):
        if travelling e relaxes distance to u:
            relax dist[u]
            if e.weight = 1:
                d.push_back(u)
            else:
                d.push_front(u)

시간 복잡도 $O(E + V)$

Dijkstra

가중치에 음수가 없는 경우 선택
- 그리디 기반인데, 음수 가중치가 있으면 그리디 논리에 모순이 발생
- 사이클이 없으면 구현이 가능할 수 있지만 시간 복잡도가 큼 $O(V^2)$
- 음수의 사이클이 존재할 때는 무한 루프 문제 발생
그리디 + DP 기반 ⇒ 우선순위 큐 사용

Bellman Ford

가중치에 음수가 있는 경우 선택
- 벨만 포드도 음수 사이클이 있다면 최단 경로 구할 수 없고 “탐지”는 가능
모든 간선을 반복적으로 탐색하면서 최단 경로를 점진적 업데이트하는 방식
간선 수 (E)가 적을 때 사용
시간복잡도 : $O(VE)$

Floyd-Warshall

가중치에 음수가 있고 모든 정점 쌍의 최단 경로를 구할 때
- 음수 사이클 X ⇒ 경로 길이 무한으로 수렴
DP 기반의 알고리즘
시간복잡도 : $O(V^3)$

최소 스패닝 트리 Minimum Spanning Tree

우선 스패닝 트리가 무엇일까?

스패닝 트리 Spanning Tree

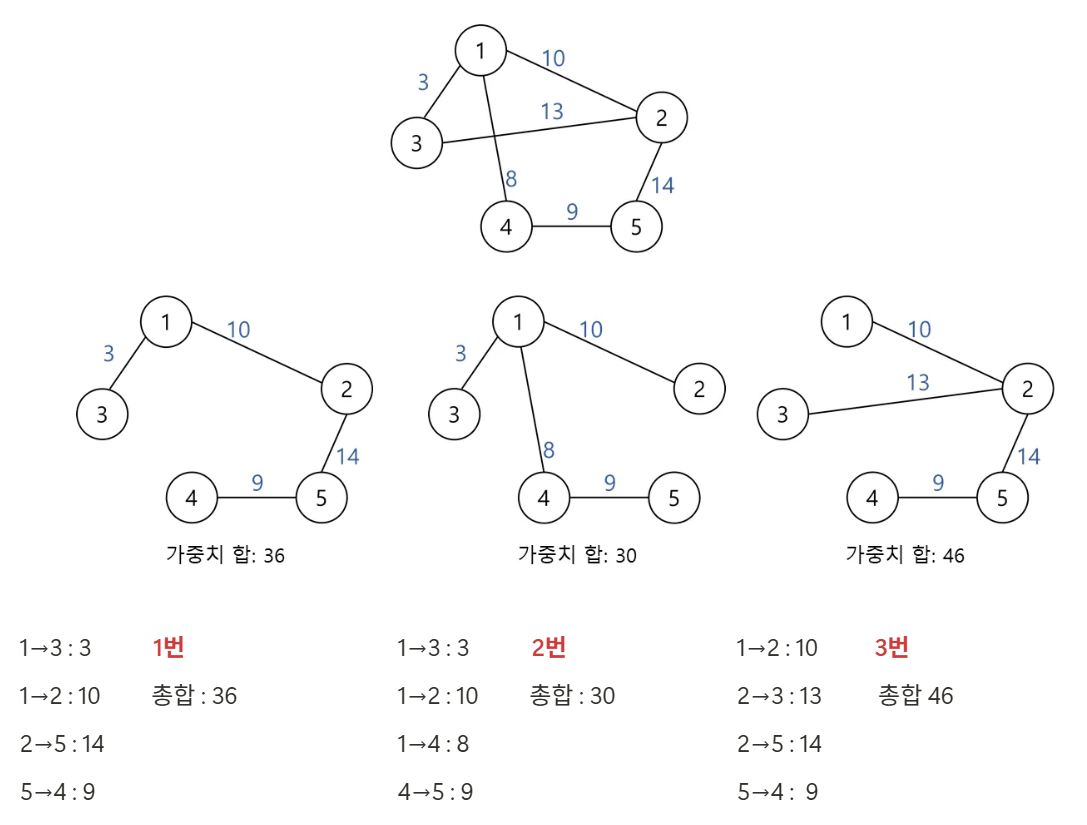
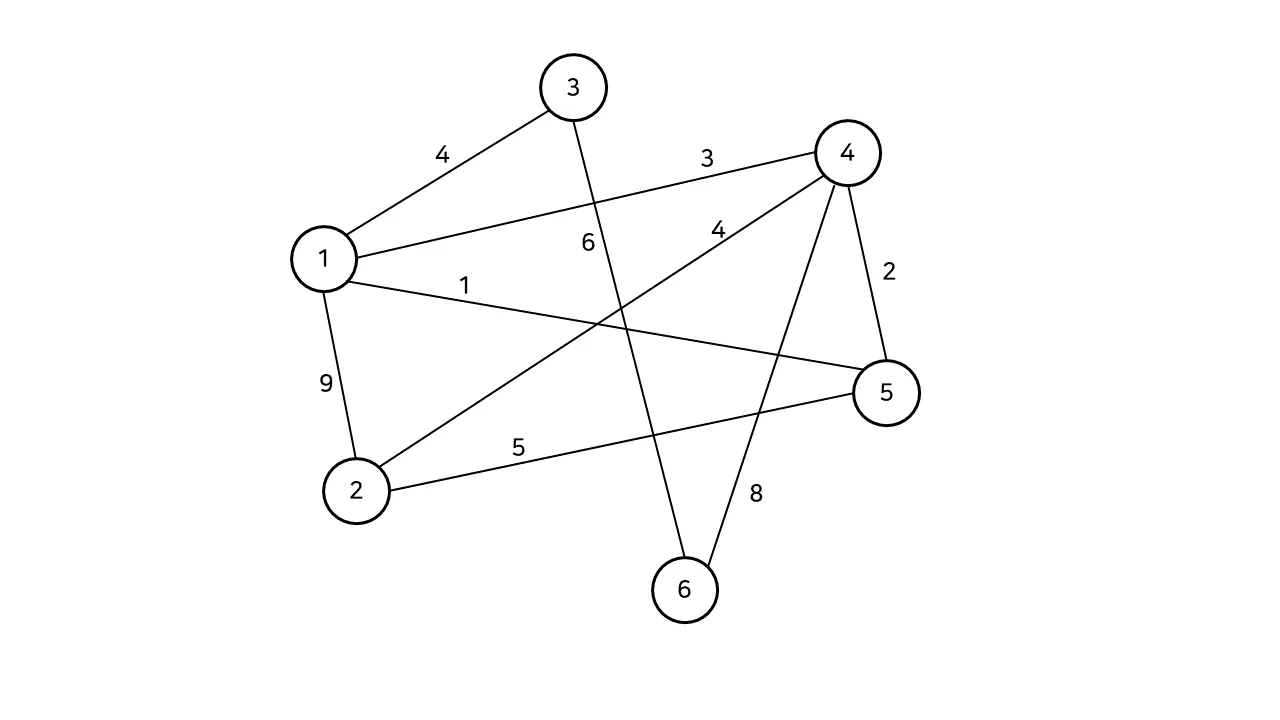
정의 = “n개의 정점으로 이루어진 무향 그래프에서 n개의 정점과 n-1개의 간선을 이루어진 트리”
1번 / 2번 / 3번 = 모든 노드를 지나는 경로 중 골라봄. (여러 스패닝 트리 존재 가능)
사이클이 없음
정점의 개수 n 일 때? 스패닝 트리의 간선 개수는? 당연히 n-1 개
사용하는 이유
- 네트워크 설계 : 최소 케이블로 모든 컴퓨터 연결하는 네트워크 설계
- 소셜 네트워크 분석 : 중요 노드 간의 연결 분석 후 군집 구조 단순화로 시각화
- 데이터 압축 : 이미지 데이터를 그래프로 표현 후 스패닝 트리 생성해 연결된 주요 픽셀 정보만 보관하는 방식으로 데이터를 압축

최소 + 스패닝 트리 ➡️ 스패닝 트리 中 가장 작은 것
의미는 쉬운데 막상 코드 작성 시 어려움…
작성 방식은 크게 두 가지 ⇒ **KRUSKAL / PRIM

왜 완전탐색은 안될까?

최소 신장 트리를 완전 탐색으로 생각

정점 30개, 간선 60개라 생각할 때 완전 탐색해서 MST 찾아보면?

$_{60}C_{29}$ ⇒ 터쳐버림

KRUSKAL

💡
[중요 정보]

구현 : 정렬 + 그리디 + 유니온 파인드

시간 복잡도 : $O(ElogE)$

간선이 적은 희소 그래프 에서 효율적

간선에 관심이 있음
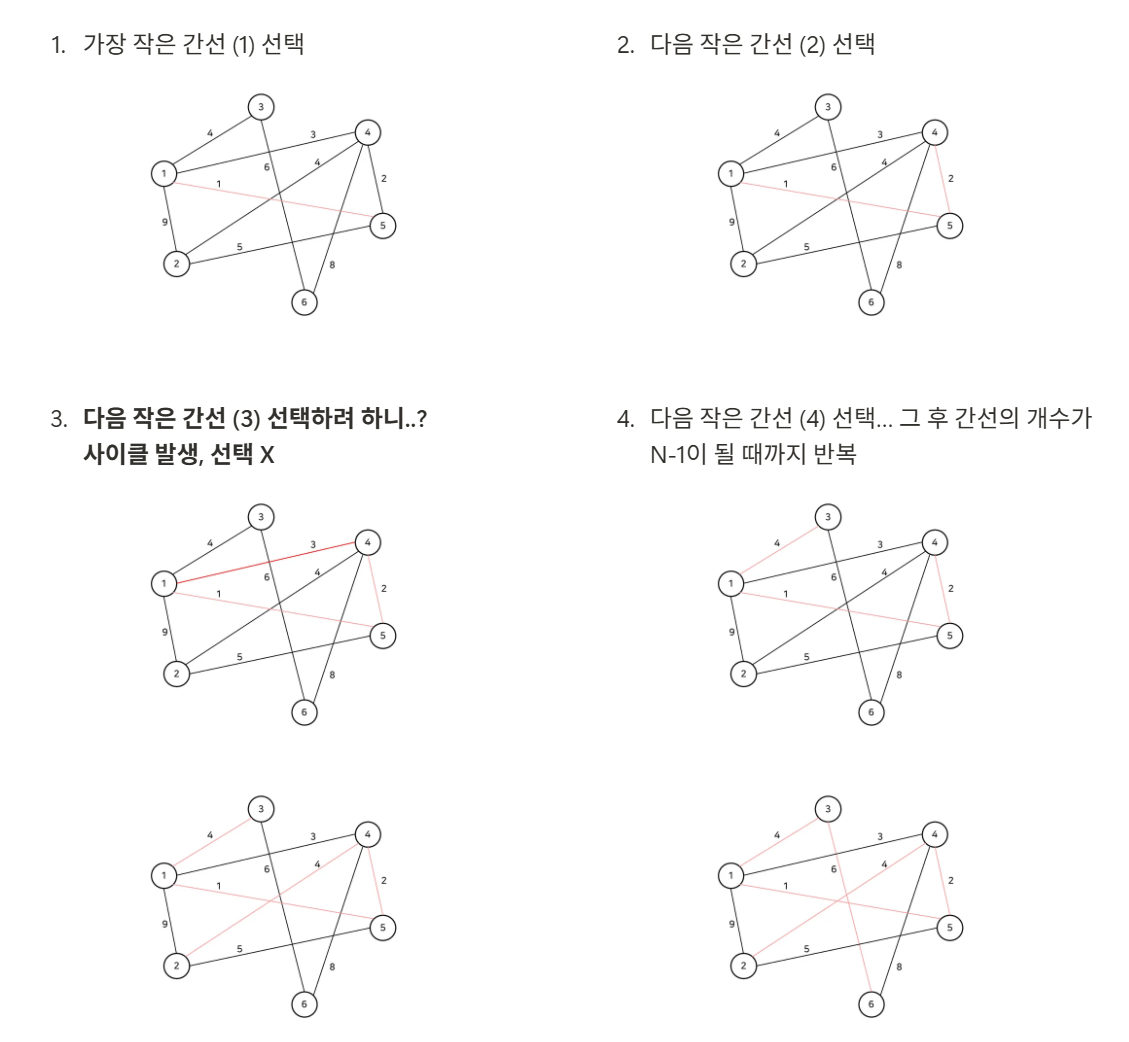
💡아이디어💡
[1, 10, 2, 3, 4] 에서 3개를 뽑아 합이 최소가 되는 경우?
⇒ 정렬 (오름차순)
⇒ 앞쪽부터 3개 선택 : 그리디
⇒ 근데 사이클이면 안되는데…. : 유니온 파인드
예제

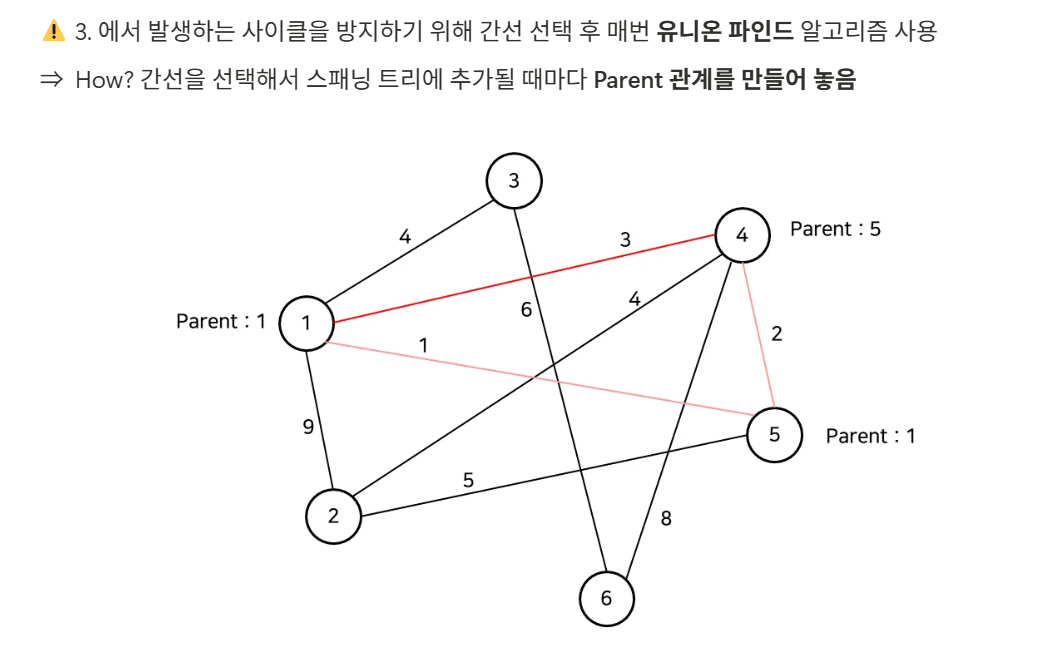
import java.util.*;

class Edge implements Comparable<Edge> {
    int src, dest, weight;

    public Edge(int src, int dest, int weight) {
        this.src = src;
        this.dest = dest;
        this.weight = weight;
    }

    @Override
    public int compareTo(Edge other) {
        return this.weight - other.weight; // 가중치 오름차순 정렬
    }
}

public class KruskalMST {
    static int[] parent;

    // 유니온-파인드: Find 연산
    public static int find(int node) {
        if (parent[node] == node) return node;
        return parent[node] = find(parent[node]); // 경로 압축
    }

    // 유니온-파인드: Union 연산
    public static void union(int node1, int node2) {
        int root1 = find(node1);
        int root2 = find(node2);
        if (root1 != root2) {
            parent[root2] = root1; // 두 집합을 합침
        }
    }

    public static void main(String[] args) {
        int vertices = 5; // 정점 개수
        int edgesCount = 7; // 간선 개수

        // 간선 리스트 초기화
        List<Edge> edges = new ArrayList<>();
        edges.add(new Edge(0, 1, 1)); // A-B: 1
        edges.add(new Edge(0, 2, 3)); // A-C: 3
        edges.add(new Edge(1, 2, 3)); // B-C: 3
        edges.add(new Edge(1, 3, 6)); // B-D: 6
        edges.add(new Edge(2, 3, 4)); // C-D: 4
        edges.add(new Edge(2, 4, 2)); // C-E: 2
        edges.add(new Edge(3, 4, 5)); // D-E: 5

        // 유니온-파인드 초기화
        parent = new int[vertices];
        for (int i = 0; i < vertices; i++) {
            parent[i] = i; // 초기에는 각 정점이 자신이 부모
        }

        // 간선 가중치 기준 정렬
        Collections.sort(edges);

        // 크루스칼 알고리즘 수행
        List<Edge> mst = new ArrayList<>();
        int mstWeight = 0;

        for (Edge edge : edges) {
            // 사이클이 생기지 않으면 간선 선택
            if (find(edge.src) != find(edge.dest)) {
                union(edge.src, edge.dest);
                mst.add(edge);
                mstWeight += edge.weight;
            }
        }

        // 결과 출력
        System.out.println("Minimum Spanning Tree:");
        for (Edge edge : mst) {
            System.out.printf("Edge: %d-%d, Weight: %d\n", edge.src, edge.dest, edge.weight);
        }
        System.out.println("Total Weight: " + mstWeight);
    }
}

Minimum Spanning Tree:
Edge: 0-1, Weight: 1
Edge: 2-4, Weight: 2
Edge: 0-2, Weight: 3
Edge: 2-3, Weight: 4
Total Weight: 10

PRIM

💡
[중요 정보]

구현 : 그리디 + 우선순위 큐

시간 복잡도 : $O(ElogV)$

간선이 많은 밀집 그래프 에서 효율적

노드(정점)에 관심이 있음
💡 아이디어 💡
1. 시작 정점(0번) 선택
2. 연결된 간선 중에서 가중치가 가장 작은 간선 선택: 그리디 + 우선순위 큐
3. 새로운 정점 추가 → 해당 정점에서 연결된 간선 추가
4. 이미 방문한 정점으로의 간선은 무시: 방문 체크 (사이클 방지)
5. 모든 정점이 연결될 때까지 반복
예제

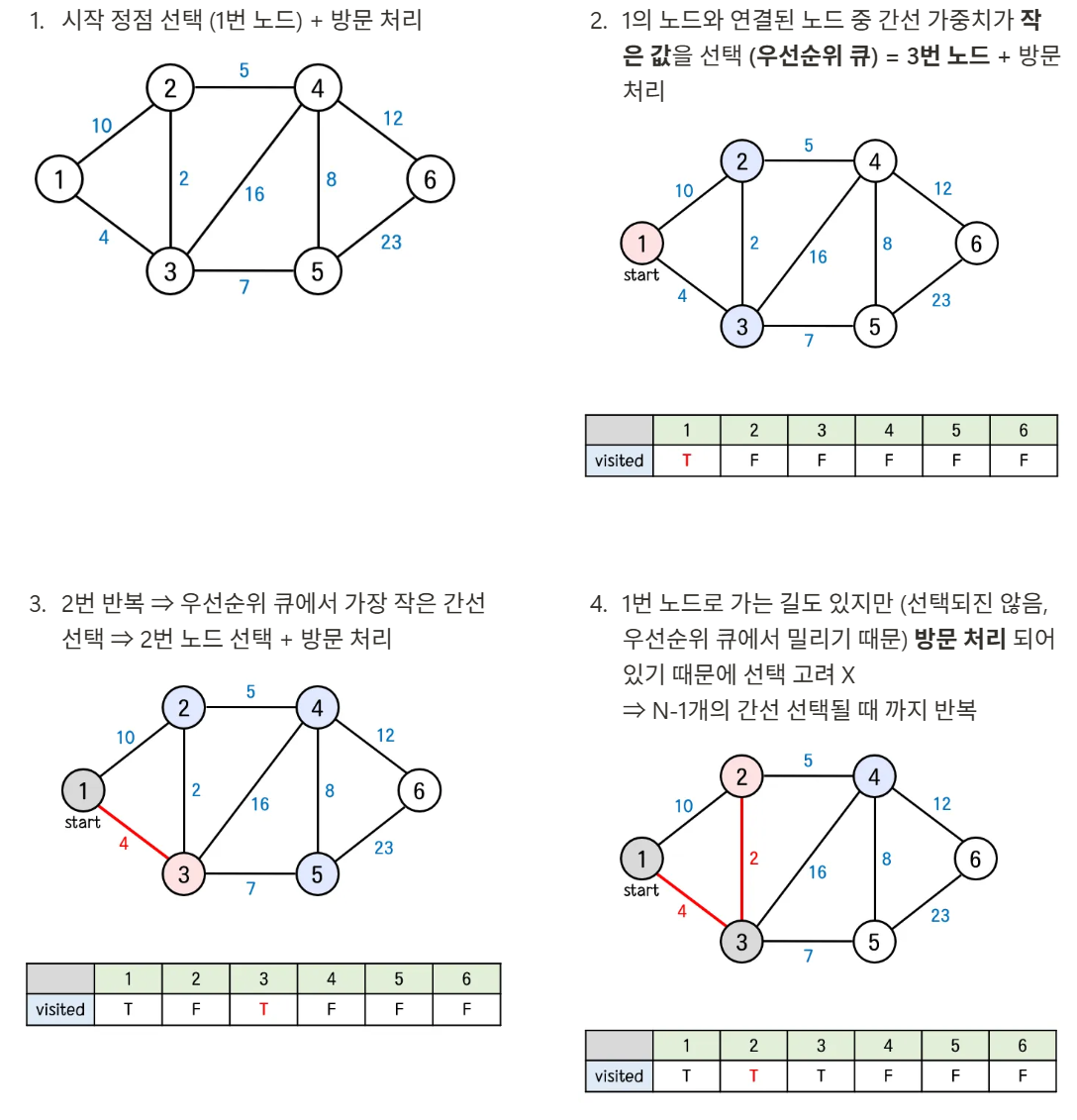
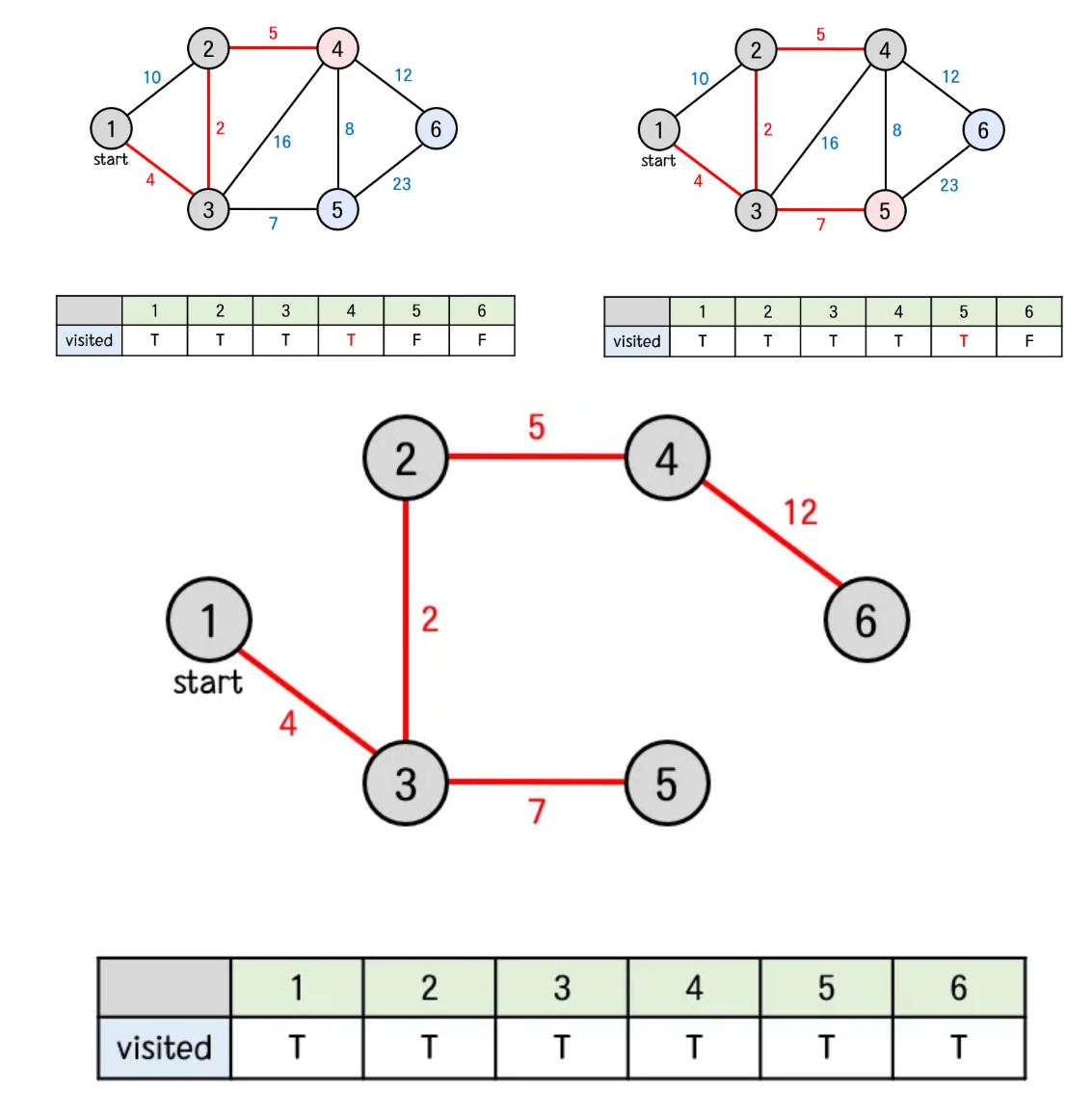
import java.util.*;

class PrimMST {
    static class Edge implements Comparable<Edge> {
        int dest, weight;

        public Edge(int dest, int weight) {
            this.dest = dest;
            this.weight = weight;
        }

        @Override
        public int compareTo(Edge other) {
            return this.weight - other.weight; // 가중치 기준 오름차순 정렬
        }
    }

    public static void main(String[] args) {
        int vertices = 5; // 정점의 개수

        // 그래프를 인접 리스트로 초기화
        List<List<Edge>> graph = new ArrayList<>();
        for (int i = 0; i < vertices; i++) {
            graph.add(new ArrayList<>());
        }

        // 간선 추가 (무방향 그래프)
        graph.get(0).add(new Edge(1, 1)); // A-B: 1
        graph.get(1).add(new Edge(0, 1));
        graph.get(0).add(new Edge(2, 3)); // A-C: 3
        graph.get(2).add(new Edge(0, 3));
        graph.get(1).add(new Edge(2, 3)); // B-C: 3
        graph.get(2).add(new Edge(1, 3));
        graph.get(1).add(new Edge(3, 6)); // B-D: 6
        graph.get(3).add(new Edge(1, 6));
        graph.get(2).add(new Edge(3, 4)); // C-D: 4
        graph.get(3).add(new Edge(2, 4));
        graph.get(2).add(new Edge(4, 2)); // C-E: 2
        graph.get(4).add(new Edge(2, 2));
        graph.get(3).add(new Edge(4, 5)); // D-E: 5
        graph.get(4).add(new Edge(3, 5));

        // 우선순위 큐를 사용하여 최소 가중치 간선을 선택
        PriorityQueue<Edge> pq = new PriorityQueue<>();

        boolean[] visited = new boolean[vertices]; // 방문 여부 체크
        int mstWeight = 0; // MST 가중치 합
        List<String> mstEdges = new ArrayList<>(); // MST 간선 리스트

        // 시작 정점 (0번 정점)
        pq.add(new Edge(0, 0));

        while (!pq.isEmpty()) {
            Edge current = pq.poll(); // 가장 가중치가 작은 간선 선택

            if (visited[current.dest]) continue; // 이미 방문한 정점이면 스킵

            visited[current.dest] = true; // 정점 방문 처리
            mstWeight += current.weight; // MST 가중치 추가

            // 간선을 기록 (시작 정점이 있는 경우 출력)
            if (current.weight != 0) {
                mstEdges.add(String.format("Edge: %d, Weight: %d", current.dest, current.weight));
            }

            // 현재 정점에 연결된 간선을 큐에 추가
            for (Edge neighbor : graph.get(current.dest)) {
                if (!visited[neighbor.dest]) {
                    pq.add(neighbor);
                }
            }
        }

        // 결과 출력
        System.out.println("Minimum Spanning Tree:");
        for (String edge : mstEdges) {
            System.out.println(edge);
        }
        System.out.println("Total Weight: " + mstWeight);
    }
}

최소 경로(비용) 알고리즘 선택 가이드

가중치 조건	알고리즘	시간 복잡도	설명
가중치 없음	BFS	O(V+E)	가중치가 없는 무향 또는 유향 그래프에서 최단 경로를 구함.
가중치 0과 1	0/1 BFS	O(V+E)	간선의 가중치가 0 또는 1로 한정될 때 효율적.
가중치 양수	다익스트라	O((V+E)log⁡V)	우선순위 큐를 활용하여 양수 가중치의 최단 경로를 효율적으로 계산.
가중치 음수 포함	벨만포드	O(VE)	음수 가중치가 있는 그래프에서도 안전하게 최단 경로 계산 가능.
모든 정점 간 최단 경로	플로이드-워셜	O(V^3)	그래프의 모든 정점 쌍 사이의 최단 경로를 구함.
MST, 모든 정점 방문 시 최소 가중치, 간선이 적은 희소 그래프	크루스칼	O(ElogE)	그리디 + 정렬 + 유니온 파인드
MST, 모든 정점 방문 시 최소 가중치, 간선이 많은 밀집 그래프	프림	O(ElogV)	그리디 + 우선순위큐