삽입
n개의 노드로 이루어진 레드-블랙 트리에서 노드 하나를 삽입하는 것은 O(logn) 시간에 수행될 수 있다.
보통의 이진 탐색 트리처럼 노드 z를 트리 t에 삽입한 뒤 z를 적색으로 칠한다.
(왜 흑색이 아닌 적색으로 칠할까?.. -> 고민해보기)
- RB tree에서 새로운 노드를 삽입할 때, 새로운 노드는 항상 적색으로 입력한다.
- 만약 트리가 레드-블랙 트리의 특성을 위반하면, 두가지 operation을 통해 트리의 구조를 조정한다.
(1) Recoloring
(2) Rotation (Restructuring)
insert 과정
키 값이 20인 노드를 삽입하는 과정을 생각해보자
*중요! target 노드를 주시하자
key = 20인 노드가 들어갈 위치 탐색 후 삽입

insert fixup 과정
*중요! while문 조건->target의 부모가 적색일 때
CASE 1. 부모 노드의 컬러 Red & 삼촌 노드의 컬러 Red
- target node(20) color:
red - parent color(28):
red
이는 RB tree 특성4. 적색 노드의 자식은 무조건 흑색이다. 위배!
그리고 확인해야 할 것!
grandparent(18)의 다른 자식인 uncle node의 색상 - uncle node(12) color:
red
👉🏻 parent & uncle 모두 red! (CASE 1)
recoloring 진행
👉🏻 parent & uncle:black으로 변경 + grandparent:red로 변경
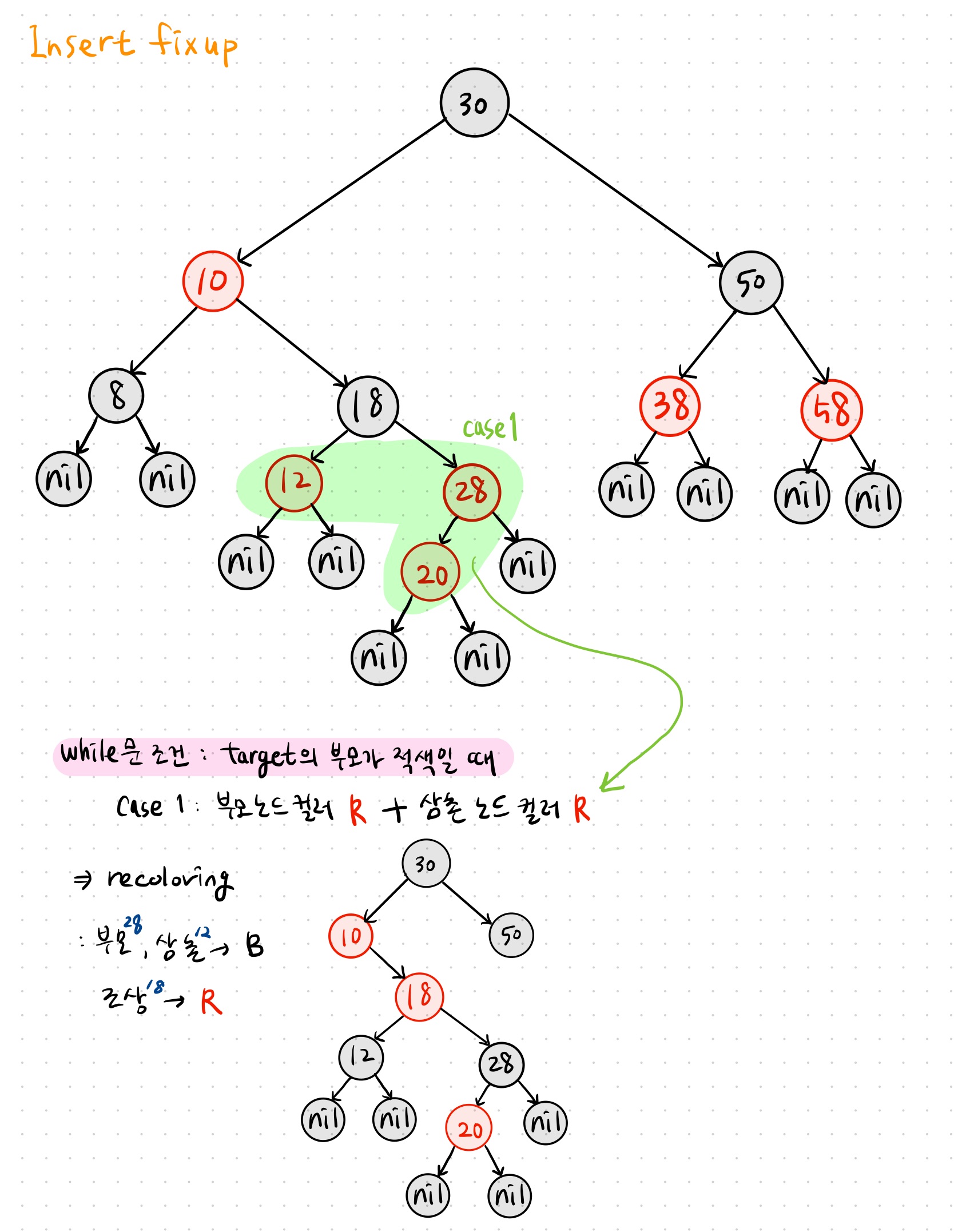
CASE 2. 부모 노드의 컬러 Red & 삼촌 노드의 컬러 Black
- target node(18) color:
red - parent color(10):
red
이는 RB tree 특성4. 적색 노드의 자식은 무조건 흑색이다. 위배! - uncle node(50) color:
black
👉🏻 parent: red & uncle black! (CASE 2)
부모노드(10)를 target node로 설정 후, left rotate!
target = 10 -> 좌회전
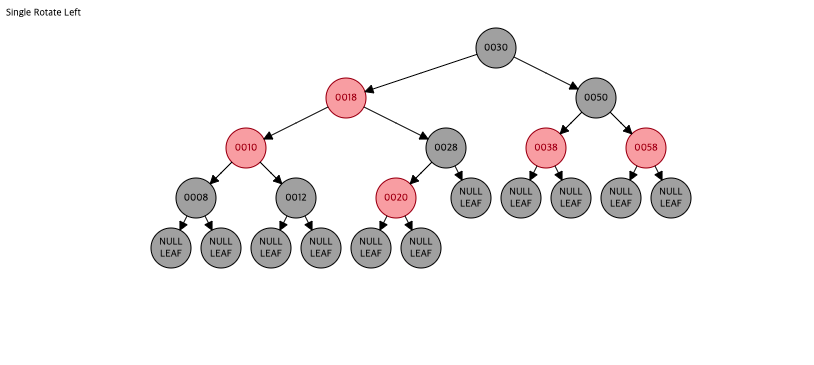
여기까지 하면 case2-(1)이다.
but.. 이 상태라면 RB tree 특성4 & 특성5를 위배..
case2-(1) 인 경우에는 이어서 case2-(2) 를 진행한다고 생각하면 된다.
case2-(2) 는 부모노드가 할아버지 노드의 왼쪽 자식이며, target 또한 부모노드의 왼쪽 자식일 때다. (or 오른쪽 자식의 오른쪽 자식이 target일 때) -> 이는 일렬로 나열된 상태를 말한다.
정리해보면,
① Fix up 과정은 부모노드가 red일 때 일어난다. (나는 new node이므로 항상 red)
② case1은 parent & uncle 둘 다 red
③ case2는 parent: red & uncle: black일 때 아래와 같이 2가지로 나뉜다.
case2-(1) : 꺾새 모양
grandparent -> left -> right = target 또는 grapndparent -> right -> left = target
부모노드가 왼쪽 자식이면 left rotation / 오른쪽 자식이면 right rotation
case2-(2) : 일렬
grandparent -> left -> left = target 또는 grandparent -> right -> right - target
부모노드가 왼쪽 자식이면 right rotation / 오른쪽 자식이면 left rotation
처음부터 바로 case2-(2) 형태가 될 수도 있고, case2-(1) 형태이면 이어서 case2-(2)를 바로 진행하게 된다.
그럼 이어서 다시!

여기까지가 case2-(1)까지 진행한 상태이므로 이어서 case2-(2)를 진행해보자
10, 18, 30을 봤을 때
case2-(2): grandparent -> left -> left = target
- target = 10
- parent = 18
- grandparent = 30
rotation 진행
👉🏻 부모노드가 조상의 왼쪽 자식이면 right rotation / 오른쪽 자식이면 left rotation !!!
recoloring 진행
👉🏻 부모노드(18) black 으로 변경 + 조상노드(30) red 로 변경!
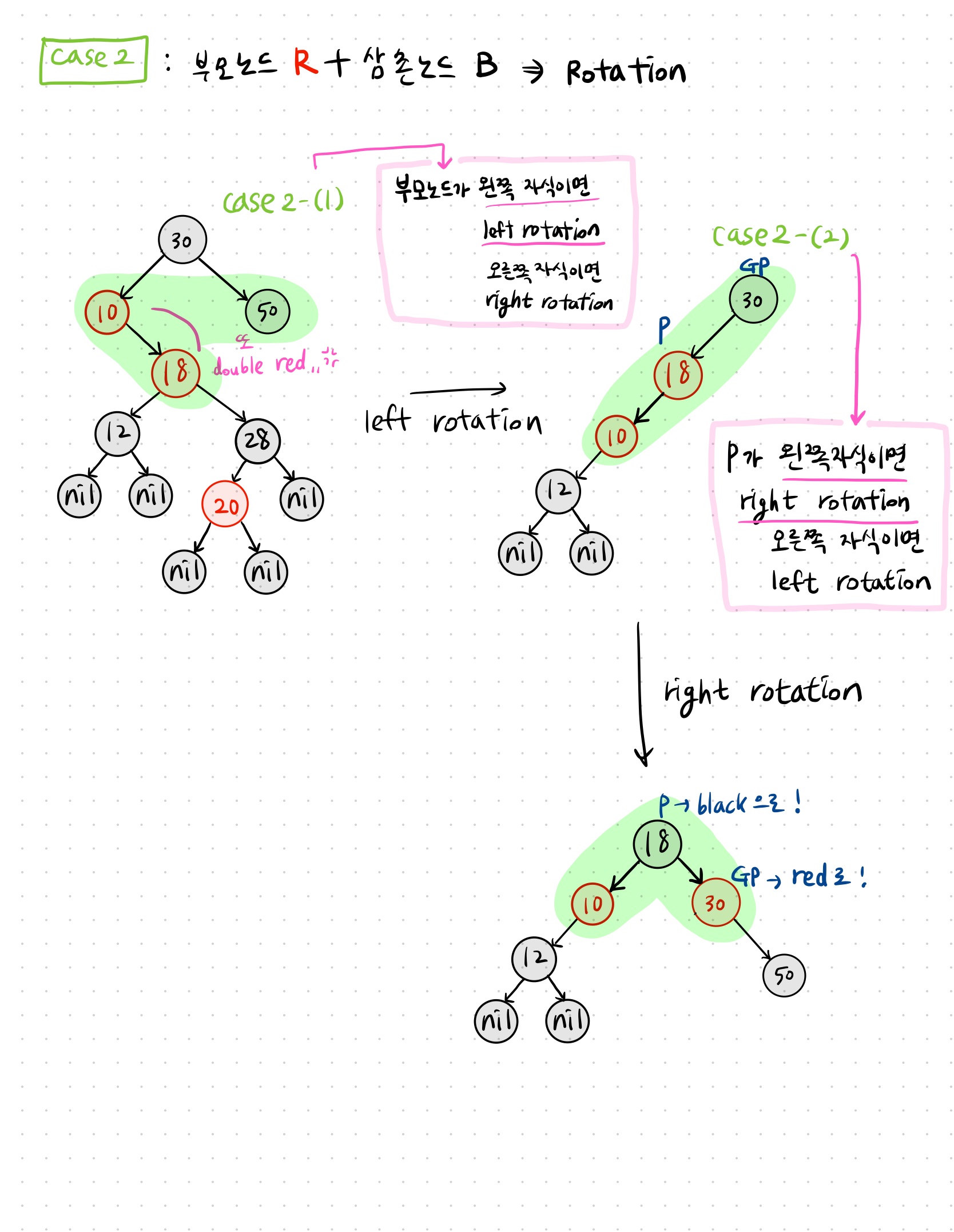
초반에 설정한 while문 조건이 target의 parent가 red일 때다.
parent(18)는 root이므로 black이다. 따라서 while문 종료!
이로써 레드-블랙 트리의 특성을 전부 만족하는 트리가 완성되었다!!!!
insert 슈도코드
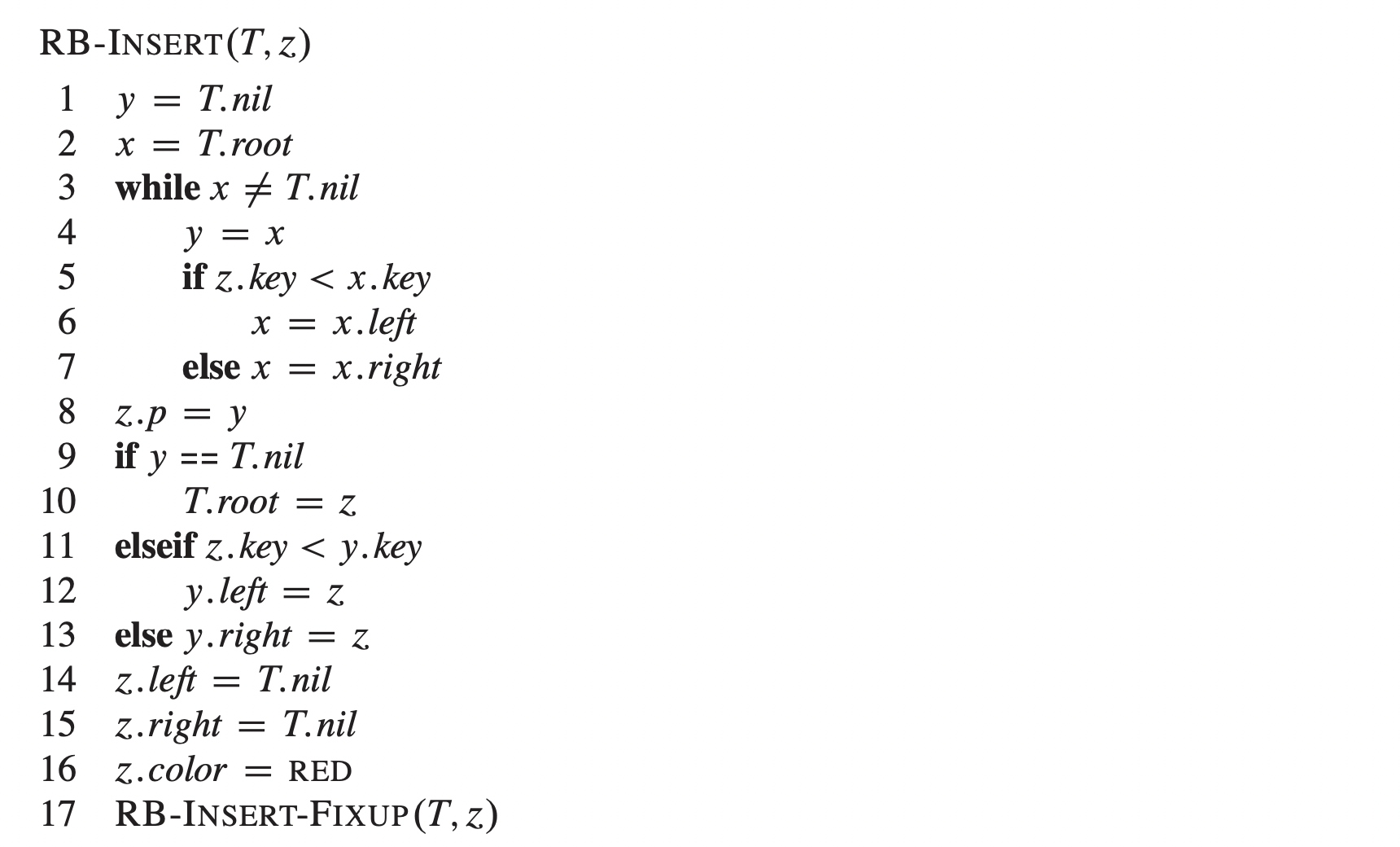
insert fixup 슈도코드

🚨주의! fixup 슈도코드에서 else if는 else안에 또다른 if문을 나타냄
작성한 코드
insert
// 데이터 삽입
node_t *rbtree_insert(rbtree *t, const key_t key) {
node_t *x = t->root; // 트리의 루트 노드
node_t *y = t->nil; // 트리의 nil 노드
while (x != t->nil) { // x가 리프노드에 도달할 때까지 반복
y = x; // tmp 역할 (nil을 만나기 직전노드의 값에 z를 넣어줘야돼서 y에 저장)
if (key < x->key) { // 만약 x의 key값보다 삽입할 key값이 작으면
x = x->left; // x를 x의 왼쪽으로 변경
}
else // 만약 x의 key값보다 삽입할 key값이 크거나 같으면
x = x->right; // x를 x의 오른쪽으로 변경
}
// while문 종료 = x가 nil을 가리킴 -> new_node(z) 삽입할 시기
node_t *z = (node_t*)calloc(1, sizeof(node_t)); // z 노드 생성
z->key = key; // z의 키값을 넣어줌
z->parent = y; // z의 부모는 미리 저장해놓은 y
if (y == t->nil) // y가 트리의 nil = 비어있던 애
t->root = z; // 루트는 z
else if (z->key < y->key) // y의 key값이 z의 key값보다 크면
y->left = z; // z는 y의 왼쪽 자식
else // y의 key값이 z의 key값보다 작거나 같으면
y->right = z; // z는 y의 오른쪽 자식
z->left = t->nil; // z의 왼쪽 자식 nil
z->right = t->nil; // z의 오른쪽 자식 nil
z->color = RBTREE_RED; // new_node는 늘 red
rbtree_insert_fixup(t, z);
return t->root;
}insert_fixup
// insert_fixup (색 변경)
void rbtree_insert_fixup(rbtree *t, node_t *z) {
while (z->parent->color == RBTREE_RED) { // z의 부모가 red (double red)
if (z->parent==z->parent->parent->left) {
node_t *uncle = z->parent->parent->right;
// CASE 1 = 부모 R + 삼촌 R
if (uncle->color == RBTREE_RED) { // 삼촌 레드일 때
z->parent->color = RBTREE_BLACK;
uncle->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
z = z->parent->parent; // 조상은 무조건 red, red여야 while문 돈다!
}
else if (uncle->color == RBTREE_BLACK) { // 삼촌 블랙일 때
// CASE 2-(1) = 꺾새 모양일 때
if (z == z->parent->right) { // 타켓이 오른쪽 자식이면
z = z->parent; // 타켓을 그 부모로 바꾸고
left_rotation(t, z); // left 로테이션 고고
}
// CASE 2-(2) = 일렬일 때
z->parent->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
right_rotation(t, z->parent->parent); // 조상 기준 우회전
}
}
// z의 부모가 z조상의 오른쪽이면 위의 과정 반대로 하면 됨
else if (z->parent==z->parent->parent->right) {
node_t *uncle = z->parent->parent->left;
// CASE 1 = 부모 R + 삼촌 R
if (uncle->color == RBTREE_RED) {
z->parent->color = RBTREE_BLACK;
uncle->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
z = z->parent->parent;
}
else if (uncle->color == RBTREE_BLACK) {
// CASE 2-(1) = 꺾새 모양일 때
if (z == z->parent->left) {
z = z->parent;
right_rotation(t, z);
}
z->parent->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
left_rotation(t, z->parent->parent);
}
}
} // while문 종료
t->root->color = RBTREE_BLACK; // root는 항상 black
return; // void형
} 알게된 점
Q. new node는 왜 항상 red일까?
A. red를 삽입했을 때 RB tree의 5번 특성에 위배되지 않는다. 5번 속성은 특정 노드를 선택했을 때, 자신과 nil노드를 제외한 마주치는 black 노드의 개수가 모두 같아야 한다는 특성이다.
red 노드를 삽입할 때는 4번 속성을 위반하지만, 훨씬 간단하게 해결되는 문제이기에 red를 삽입하는 것이다!
black을 삽입하면 양쪽 서브트리의 균형을 계속 확인해야하고.. 복잡할 것 같은..? 아무튼 더 공부해봐야겠다.
