삭제를 구현하기 전에 rbtree 특성을 다시 한번 짚어보자
레드-블랙 트리의 특성
- 모든 노드는 빨간색 혹은 검은색이다.
- 루트 노드는 검은색이다.
- 모든 리프 노드(NIL)들은 검은색이다.
*NIL: null leaf, 자료를 갖지 않고 트리의 끝을 나타내는 노드- 빨간색 노드의 자식은 검은색이다.
== No Double Red(빨간색 노드가 연속으로 나올 수 없다)- 모든 리프 노드에서 Black Depth는 같다.
== 리프노드에서 루트 노드까지 가는 경로에서 만나는 검은색 노드의 개수가 같다.
삭제
레드블랙 트리에서 노드를 삭제하는 것은 삽입 연산보다 다소 복잡하다.
delete 과정에서는 이진 탐색 트리의 특성을 만족하면서 노드를 삭제할 것이다. 이후에 delete_fixup 과정에서 이진 탐색 트리의 특성과 RB트리의 특성을 모두 만족시키기 위해 트리의 구조를 변형할 것이다.
노드가 n개인 레드블랙 트리에 대한 다른 기본 연산과 마찬가지로 한 노드를 삭제하는 연산은 O(logn) 시간에 수행된다.
레드블랙 트리에서 노드를 삭제하는 프로시저는 tree-delete 프로시저를 기반으로 한다. 먼저 tree-delete가 호출하는 서브 루틴인 transplant 서브 루틴을 레드블랙 트리에 적용할 수 있도록 수정해야 한다.
삭제 과정에서 두가지 상황이 빈번하게 일어나는데, 이를 함수화 시켜놓은 슈도코드를 먼저 확인해보자!
delete
delete 슈도코드

transplant
삭제할 노드: target
target 노드는 루트노드가 아니라면 parent 노드의 왼쪽 or 오른쪽 자식일 것이다.
각각의 노드들은 parent, left, right, key, color 필드를 갖고있다. 이식과정에서는 target노드와 그 노드의 parent 노드의 연결관계만을 처리하는 과정이다.
target 노드의 후계자를 구했다고 가정하고 target의 parent 입장에서 왼쪽 자식이었는지, 오른쪽 자식이었는지 파악한 후에 그 자식을 대체할 노드로 지정한다. 대체할 노드 또한 target의 parent를 부모노드로 지정하여 두 노드를 연결한다.
RB-Transplant 프로시저와 Transplant 프로시저는 두 가지 다른 점이 있다.
첫째, 1행에서 NIL 대신 경계노드 t.nil을 참고한다.
둘째, 7행에서 조건 없이 z->parent에 값이 할당된다.
즉, z가 경계 노드를 가리키고 있어도 z->parent에 값을 설정할 수 있다. 이렇게 z=t.nil일 때도 z->parent에 값을 할당할 수 있다는 점을 유용하게 사용한다.
rb_transplant(t, target, succ)
target 삭제 후 succ 를 후임자로 지정
if (target->parent == t.nil) // 삭제할 노드가 루트일 때
t.root = succ // 트리의 루트노드를 succ으로 설정
else if (target == target->parent->left) // target이 부모의 왼쪽 자식일 때
target->parent->left = succ // 삭제할 노드의 왼쪽 자식을 succ으로
else // 오른쪽 자식일 때
target->parent->right = succ // 삭제할 노드의 오른쪽 자식을 succ으로
succ->parent = target->parent // 삭제할 노드의 부모노드를 succ의 부모노드로 설정 (연결)find_successor(t, x)
삭제할 x의 후계자를 찾는다.
왼쪽 or 오른쪽 상관은 없지만 나는 오른쪽에서 선택할 것이기 때문에 오른쪽 서브트리에서 가장 작은 값(min)을 찾는 코드를 작성하였다.
node_t *succ = x; // x의 후계자
while (succ->left != t->nil) {
succ = succ->left;
}
return succ;delete fixup (삭제 후 수정)
만일 삭제 과정에서 삭제된 노드가 red 라면, 삭제해도 black height의 변화가 없기 때문에 RB tree의 특성을 위반하지 않는다.
따라서 삭제된 자리에 transplant 과정만 거치면 된다!
다시 말하면, fixup 과정은 삭제된 노드의 색이 black일 때만 해당된다.
fixup 과정의 중심이 되는 노드는 x다.
case 1, case 2 에서 x 노드는 대체되는 노드이다.
case 3 에서 x 노드는 대체되는 노드의 오른쪽 자식이다.
delete fixup 슈도코드

RB-tree 삭제 과정
- 삭제 전 RB tree 속성을 만족한 상태여야 한다.
- 삭제 방식은 일반 BST와 동일하다.
- 삭제 후 RB tree 속성의 위반 여부를 확인한다.
- RB tree 속성을 위반했다면 재조정한다.
- RB tree 속성을 다시 만족
3번-> RB tree에서 노드를 삭제할 때 어떤 색이 삭제되는지가 속성 위반 여부를 확인할 때 매우 중요!
- 삭제하려는 노드의 자녀가 0 or 1 👉🏻 삭제되는 색 = 삭제되는 노드의 색
- 삭제하려는 노드의 자녀가 2 👉🏻 삭제되는 색 = 삭제되는 노드의 successor의 색
여기서! 삭제되는 색이 red 라면 어떠한 속성도 위반하지 않기에 상황 종료
#1: 모든 노드는 red 혹은 black
#2: 루트 노드는 black
#3: 모든 nil 노드는 black
#4: 노드가 red라면 자녀들은 black
#5: 임의의 노드에서 그 노드의 자손 nil 노드들까지 가는 경로들의 black 수는 같음
but, 삭제되는 색이 black이라면 #2, #4, #5 속성을 위반할 수 있다.
결국 속성을 위반했다 = 삭제되는 색이 black 이라는 의미
이제 RB트리의 속성을 위반했다면 어떻게 재조정 할 수 있는지 알아보자
RB tree 속성 위반
#2. 루트 노드는 black
루트 노드를 black으로 바꾸면 된다.
위와 같이 특수한 상황을 제외하면 #5 속성을 항상 위반하게 된다.
#5. 임의의 노드에서 그 노드의 자손 nil 노드들까지 가는 경로들의 black 수는 같다.
#5 속성을 다시 만족시키기 위해 삭제된 색의 위치를 대체한 노드에 extra black을 부여한다.
extra black
경로에서 black 수를 카운트 할 때 extra black은 하나의 black으로 카운트된다. -> 다시 5번 속성 만족
- doubly black: extra black이 부여된 black 노드
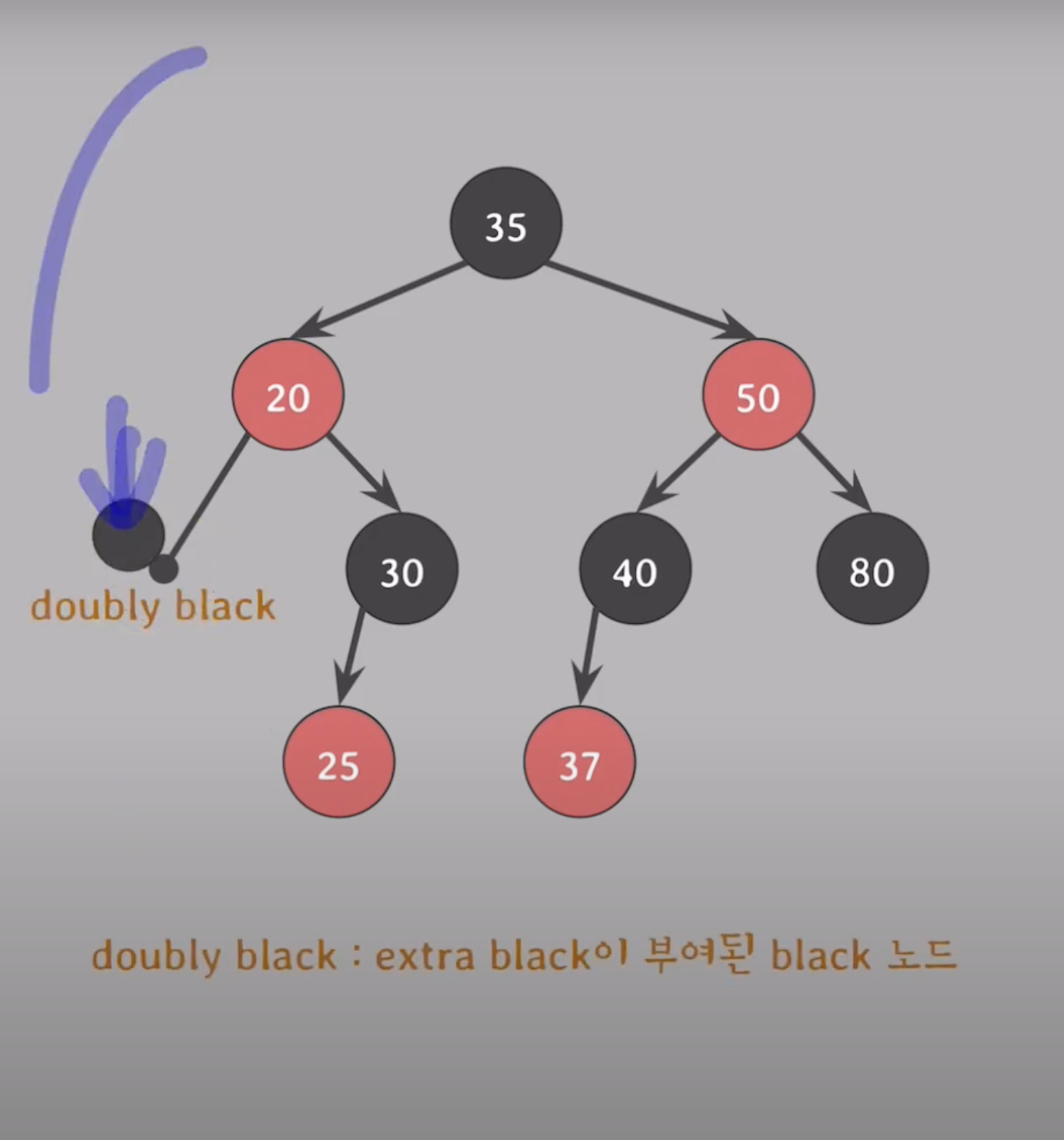
ex1) 10 삭제
10의 자녀수 0 -> 삭제되는 노드의 색은 black
이는 5번 속성을 위반하고, extra black을 부여해서 5번 속성을 다시 만족시켜야 한다.
Q. 과연 어디에 extra black을 부여해야 하나?
A. 삭제된 색의 위치를 대체한 노드
삭제된 색은 10의 black이므로 10의 위치를 대체한 노드인 nil 노드에 extra black 부여!
ex2) 50 삭제
50의 자녀수 2 -> 삭제되는 색은 50의 successor인 80의 black
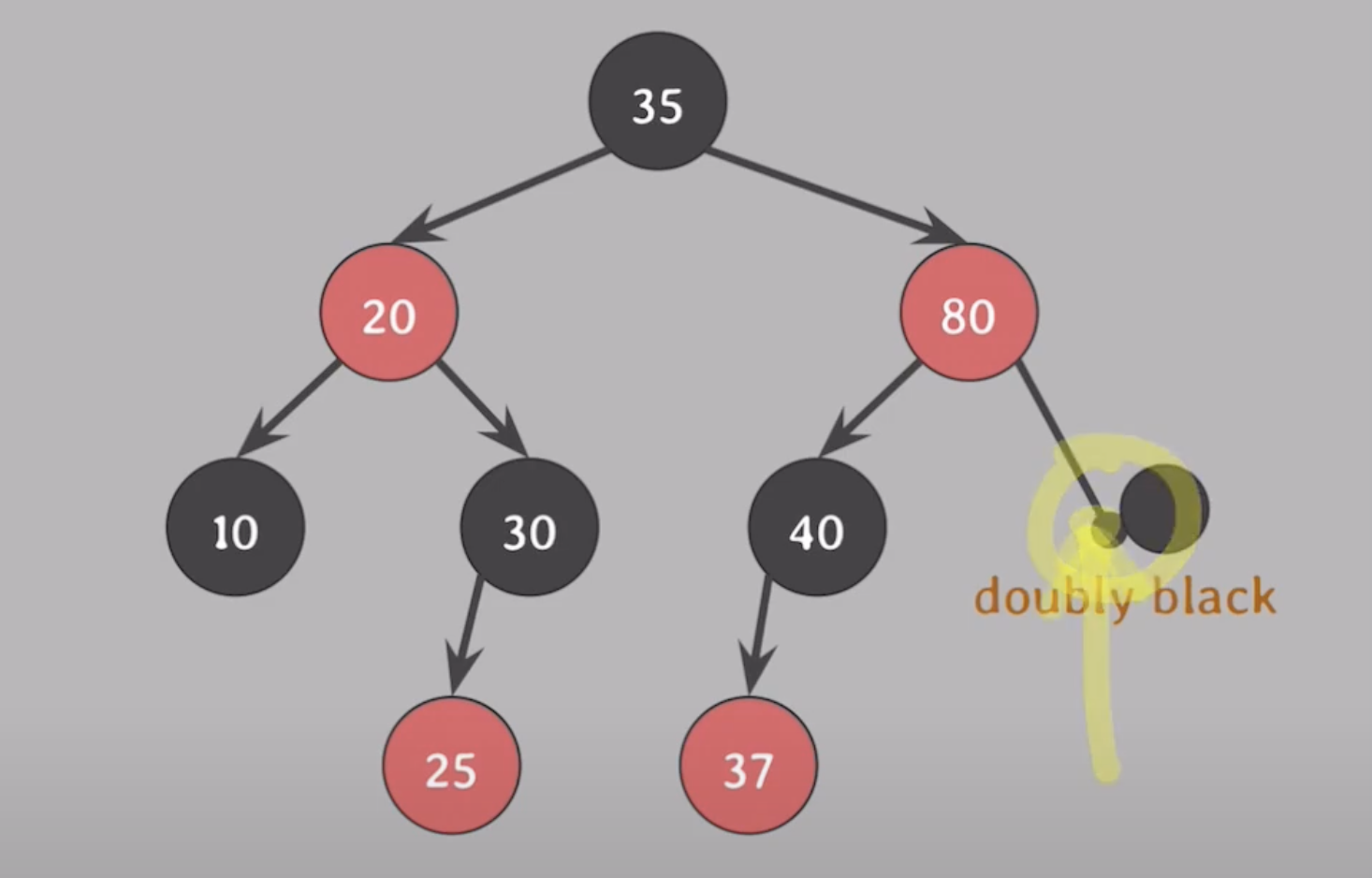
80이 원래 있던 50의 red 노드에 들어가고, 80의 위치를 대체한 nil 노드에 extra black 부여
- red-and-black: extra black이 부여된 red 노드
ex1) 30 삭제
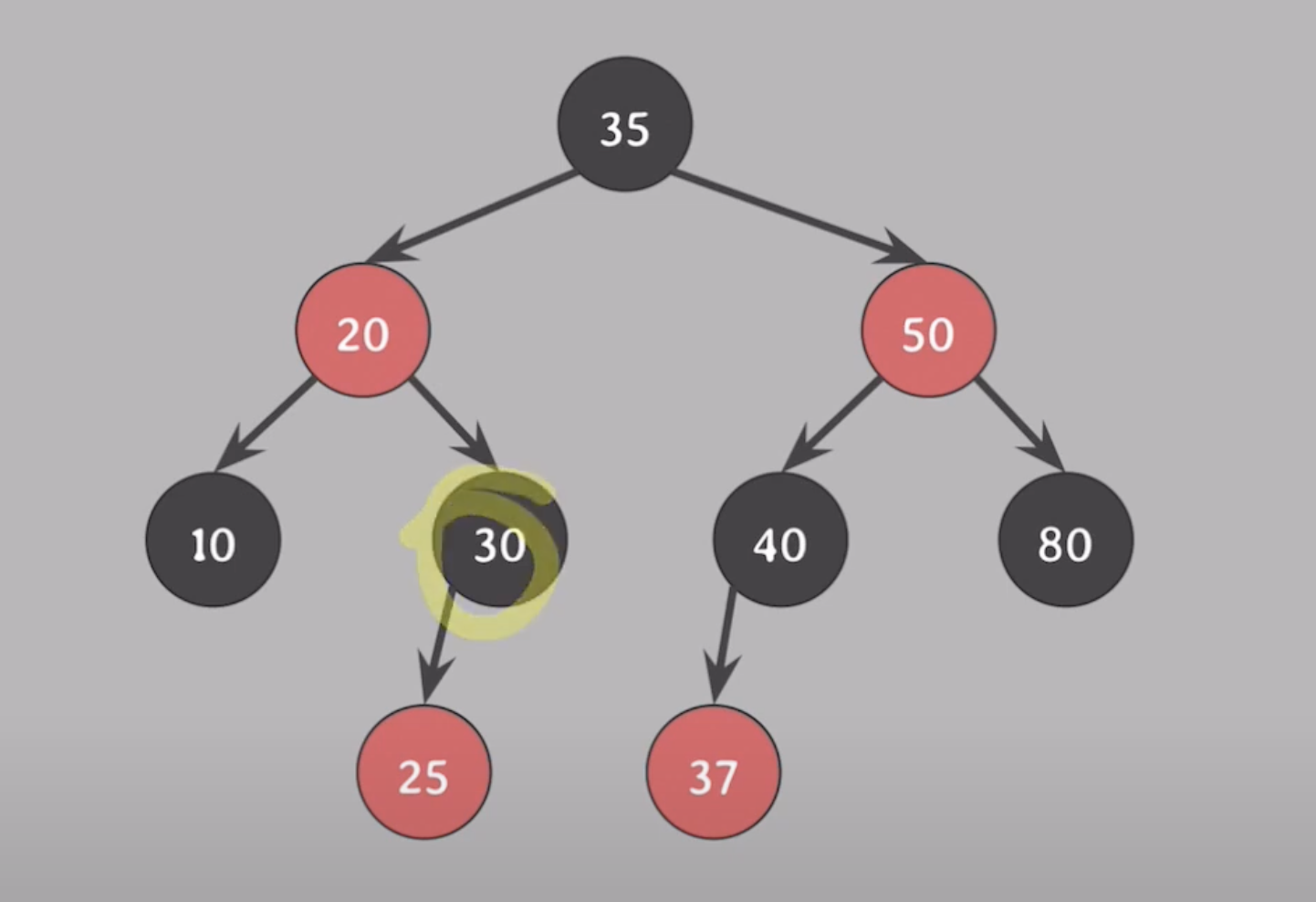
30의 자녀수 1 -> 삭제되는 노드의 색은 black
30의 위치를 대체한 노드인 25(red)에 extra black 부여!
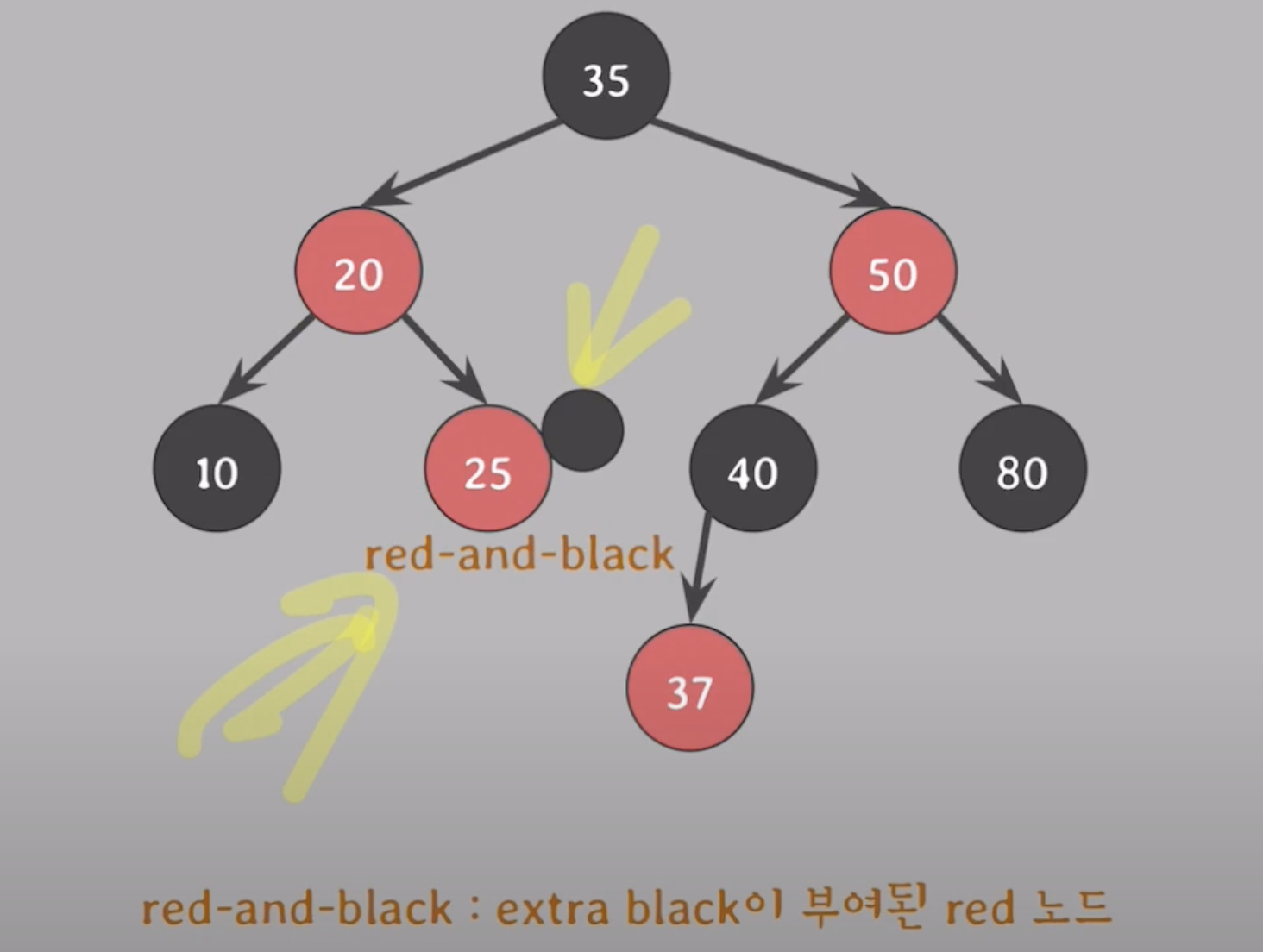
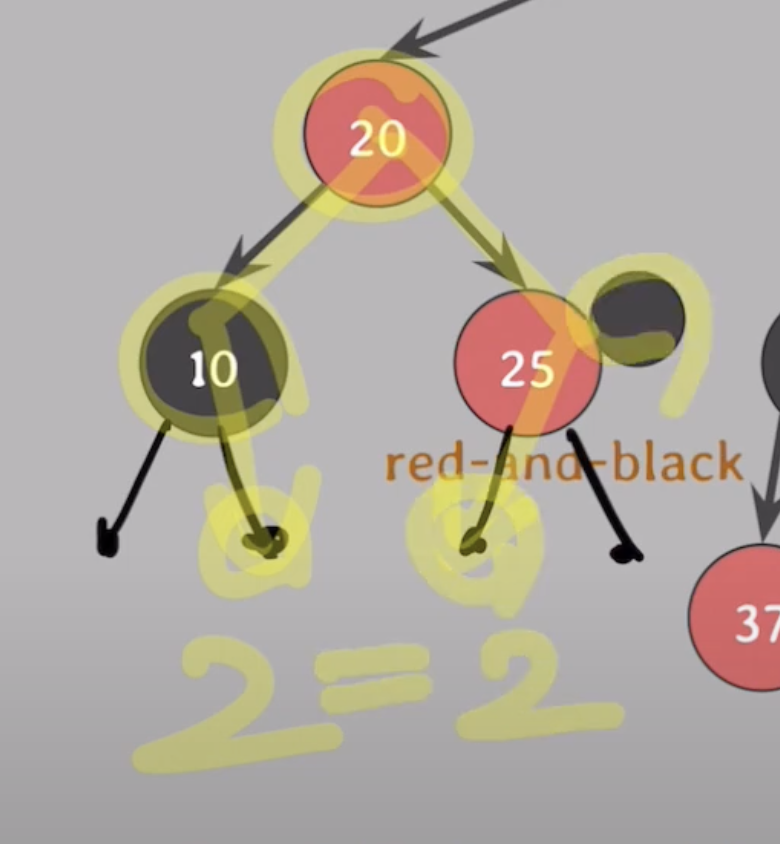
최종적으로 extra black 부여받은 노드는 doubly black이 되거나 red-and-black이 된다.
이제 이것들을 어떻게 해결할 것인가..!?
RB tree 속성 위반 해결하기
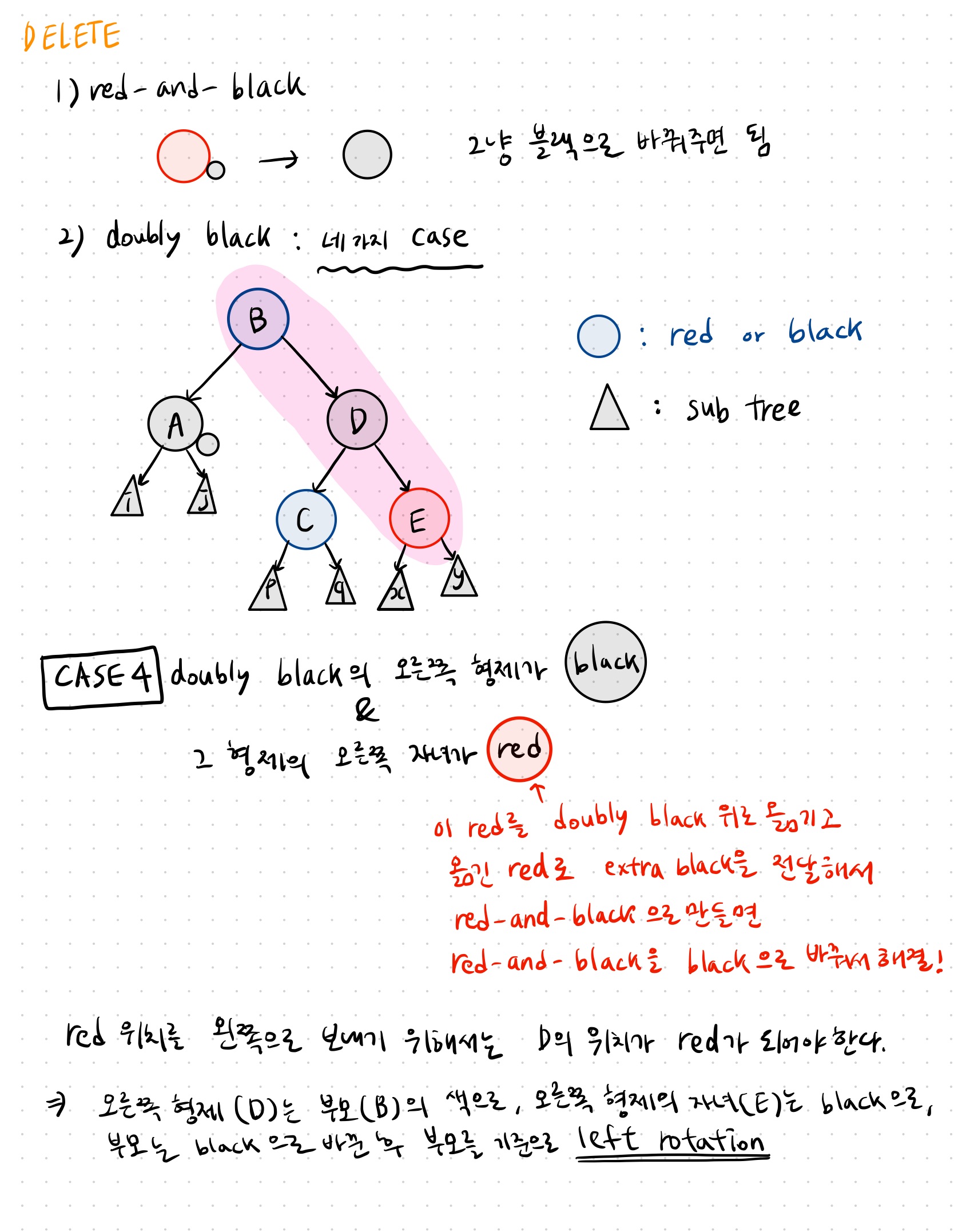
1. red-and-black 해결하기
그냥 black으로 바꿔주면 해결 ... 👉🏻 #4, #5 위반한 것을 동시에 해결!
2. doubly black 해결하기
doubly black의 extra black을 없애는 방법은 총 네가지 case로 분류됨
분류 기준 : doubly black의 형제의 색 + 그 형제의 자녀들의 색..
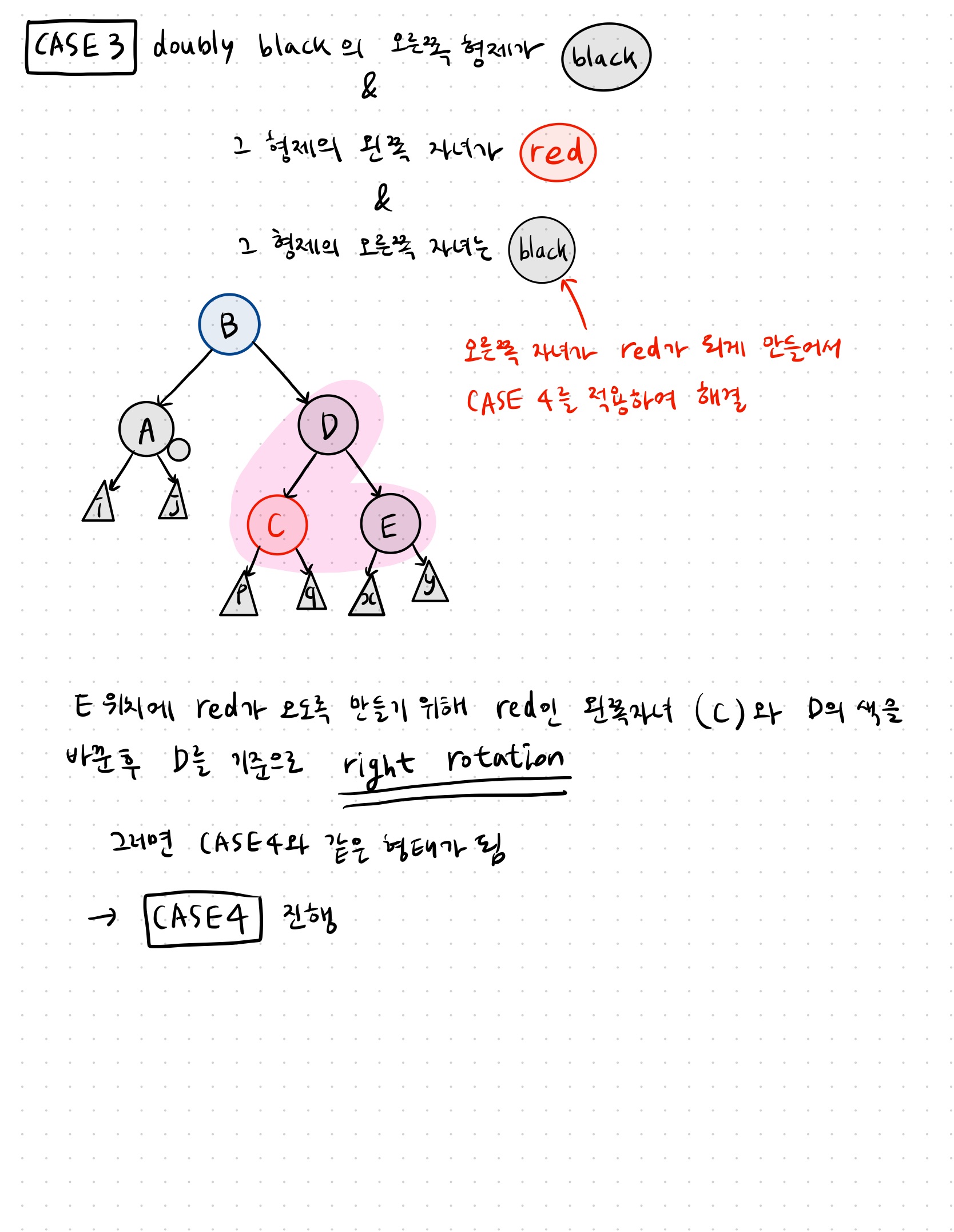
CASE 4: doubly black 오른쪽 형제 black + 그 형제의 오른쪽 자녀 red (일렬)
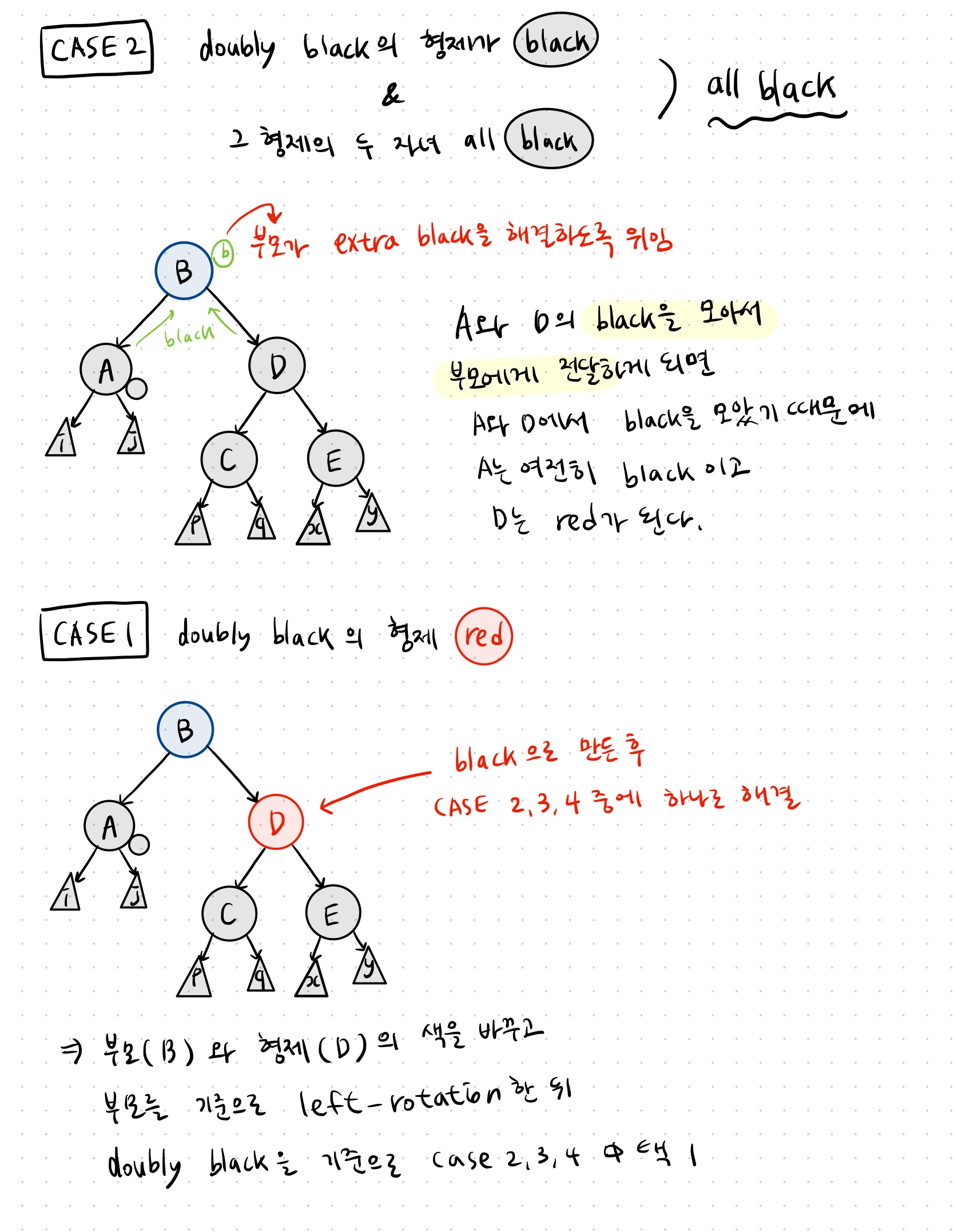
CASE 3: doubly black 오른쪽 형제 black + 그 형제의 왼쪽 자녀 red + 그 형제의 오른쪽 자녀 black (꺾새)
CASE 2: doubly black의 형제 black + 그 형제의 두 자녀 black (all black)
CASE 1: doubly black의 형제 red
작성한 코드
rbtree_erase
int rbtree_erase(rbtree *t, node_t *target) {
node_t *p = target; // 삭제할 노드를 p에 복사하여 포인터처럼 활용
color_t target_original_color = p->color; // 지워질 노드의 색을 변수에 저장
node_t *x; // succ의 값의 자리를 저장해두는 포인터, fixup의 기준이 될 노드
if (target->left == t->nil) { // 왼쪽 자식이 없을 때
x = target->right; // 정보 저장
rb_transplant(t, target, target->right);
}
else if (target->right == t->nil) { // 오른쪽 자식이 없을 때
x = target->left; // 정보 저장
rb_transplant(t, target, target->left);
}
else { // 자식 둘 다 있을 때
p = find_successor(t, target->right); // x
target_original_color = p->color; // x color
x = p->right; // nil or 값 있을수도
if (p->parent == target)
x->parent = p; // succ가 nil인 경우는 nil의 부모는 설정되지 않기 때문에 따로 지정해줘야함
else { // p의 부모가 삭제할 노드가 아닐 때
rb_transplant(t, p, p->right); // 타겟의 부모노드를 p의 오른쪽 자식과 연결
p->right = target->right; // 삭제할 노드의 오른 자식을 p의 오른쪽 자식으로 붙여줌
p->right->parent = p; // 부모도 p로 설정
}
rb_transplant(t, target, p);
p->left = target->left;
p->left->parent = p;
p->color = target->color;
}
free(target); // 할당 해제
target = NULL; // 누수 방지
if (target_original_color == RBTREE_BLACK) // 블랙 제거하면 5번특성 위반
rbtree_erase_fixup(t, x); // fixup 함수 호출
return 0;
}rbtree_erase_fixup
void rbtree_erase_fixup(rbtree *t, node_t *x) {
node_t *w;
while (x != t->root && x->color == RBTREE_BLACK) {
// 기준이 되는 노드가 왼쪽일 때
if (x == x->parent->left) {
w = x->parent->right;
// CASE 1: w 레드
if (w->color == RBTREE_RED) {
w->color = RBTREE_BLACK;
x->parent->color = RBTREE_RED;
left_rotation(t, x->parent);
w = x->parent->right;
}
// CASE 2: w 블랙, w의 두 자녀 블랙
if ((w->left->color == RBTREE_BLACK) && (w->right->color == RBTREE_BLACK)) {
w->color = RBTREE_RED;
x = x->parent;
}
// CASE 3: 꺾새 모양 w의 왼쪽 자녀 red, 오른쪽 자녀 black
else {
if (w->right->color == RBTREE_BLACK) {
w->left->color = RBTREE_BLACK;
w->color = RBTREE_RED;
right_rotation(t, w);
w = x->parent->right;
}
// CASE 4: 일렬 (최종)
w->color = x->parent->color;
w->right->color = RBTREE_BLACK;
x->parent->color = RBTREE_BLACK;
left_rotation(t, x->parent);
x = t->root; // while 종료 조건
}
}
// 기준이 되는 노드가 오른쪽일 때
else if (x == x->parent->right) {
w = x->parent->left;
// CASE 1: w 레드
if (w->color == RBTREE_RED) {
w->color = RBTREE_BLACK;
x->parent->color = RBTREE_RED;
right_rotation(t, x->parent);
w = x->parent->left;
}
// CASE 2: w 블랙, w의 두 자녀 블랙
if ((w->left->color == RBTREE_BLACK) && (w->right->color == RBTREE_BLACK)) {
w->color = RBTREE_RED;
x = x->parent;
}
// CASE 3: 꺾새 모양 w의 오른쪽 자녀 red, 왼쪽자녀 black
else {
if (w->left->color == RBTREE_BLACK) {
w->right->color = RBTREE_BLACK;
w->color = RBTREE_RED;
left_rotation(t, w);
w = x->parent->left;
}
// CASE 4: 일렬 (최종)
w->color = x->parent->color;
w->left->color = RBTREE_BLACK;
x->parent->color = RBTREE_BLACK;
right_rotation(t, x->parent);
x = t->root;
}
}
}
x->color = RBTREE_BLACK;
return;
}