Deep Learning by Ian Goodfellow: Chapter 6 (Deep Feedforward Networks)

Book: 'Deep Learning by Ian Goodfellow, Yoshua Bengio, Aa'

오늘 정리할 내용은 Chapter 6: Deep Feedforward Networks에 관한 내용이다.

서론

Deep Feedforward networks는 feedforward neural network, 혹은 MLP (Multi layer perceptron)이라고도 불린다. 순방향 신경망이라는 뜻인데, 우리가 흔히 맨 처음에 배우는 Deep Learning의 기본 모델이라고 생각하면 될 것 같다.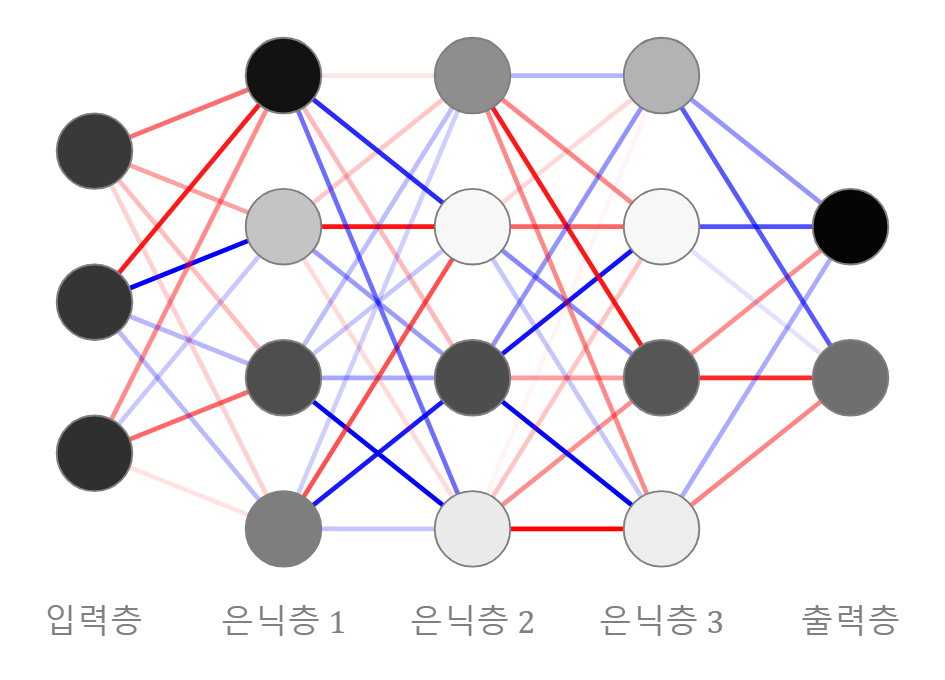

이 신경망이 input value x에서 output y로 갈 때, feedback connection이 따로 없으면 Feedforward neural network라고 불린다. 만약 이 신경망이 더 확장되어 feedback connection이 생긴다면, 그 모델은 Recurrent neural networks 라고 불린다고 한다. (Chapter 10에서 추후 공개..)

이전 logistic regression이나 linear regression 같은 문제 해결은 linear스러운 성질이 있기 때문에 수학적으로나, 예측하기 용이했다. 그러나 nonlinear적인 문제들을 해결하기 어렵다는 한계에 부딪혀, 그러한 문제들을 해결하기 위해 여러가지 접근 방법이 많이 연구되었다. 다음은 그 방법들이다.

1. SVM (Support vector machine) -> mapping function Phi를 general하게 잡아 적용함으로써 Kernel trick(RBF kernel, linear kernel, polynormial kernel etc) 사용해 해결하기

2. Engineering the mapping function Phi(Machine Learning tech without artificial neural network category). Until the advent of deep learning, it was dominant approach.

3. To learn the mapping function Phi. It is the strategy of deep learning. This can capture two adventages of Nbr 1 and 2 above

• 1. by being highly generic
• 2. Human's help with their knowledge. finding the right general function family rather than finding the right function. (engineering)

6.1 Example: Learning XOR

한마디로 요약하면 XOR은 linear model로 분류 안됨. 간단한 것이라 설명은 생략한다.

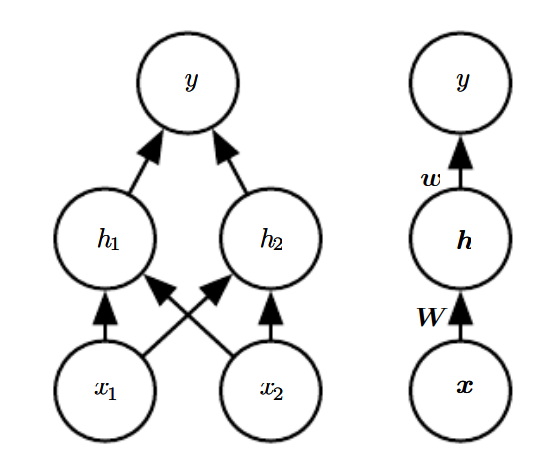
신경망 그릴 때 이렇게 두가지 방법으로 그릴수도 있다고 한다. 모델이 매우 복잡해지면 Input, weights, nodes, output들을 오른쪽처럼 나타내는 것도 좋은 방법 같다.

그리고 국밥같은 활성화함수 ReLU(Rectified Linear Unit)에 대한 간략한 설명도 담겨있었다. 이건 너무 유명한 거니까 생략함 사실 쓰기 귀찮고 너무 당연한 내용들

6.2 Gradient-Based Learning

우리가 봐온 linear model과 neural networks의 가장 큰 차이점은 neural network의 nonlinearity가 loss function을 non-convex하게 만들어준다는 것이다.

linear model은 convex optimization algorithms with guarantee of global-convergence (like SVMs)를 기반으로 하지만 neural networks는 non-convex라서 convergence가 보장되지 않기 때문에 여러 parameter들 각각에 굉장히 예민하다.

그래서 시작할 때 bias와 모든 weights들을 랜덤하게 0 혹은 아주 작은 양수값으로 지정해주는 것이 굉장히 중요하다.

6.2.1 Cost functions

음.. 그냥 별 얘기 없었고 딥러닝에서는 cost function 고르는게 중요하다는 얘기가 있었다.

6.2.1.1 Learning Conditional Distributions with Maximum Likelihood

사실 여기부터 6.2의 내용들은 대학 수준 이상의 선형대수학, 확률과통계론 내용이 주를 이뤄서 고작 학부 1학년 감자인 나는 많이 이해하지 못했다. (2학년 1학기때 배우는것들..) 그래도 노력해본 내용을 여기에 기록해보는걸로.. 올림픽 정신을 활용해보겠다.

일단 많은 neural networks는 maximum likelihood 방식을 사용해 학습한다고 한다.

추가공부 - 각종 개념들

Likelihood: 데이터가 특정 distribution으로부터 만들어졌을(generate) 확률.

어떠한 likelihood가 최대가 되는 distribution을 찾기 위해서는 주로 미분을 사용하는데, likelihood의 식이 다 곱셉으로 연결되어 있어 미분이 힘들다고 한다.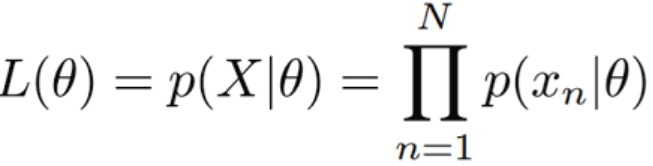

그래서 식에 negative, log을 씌워 그 값이 최소가 되는 지점을 찾음으로써 maximum likehood를 만들어주는 값을 구하는 것이다.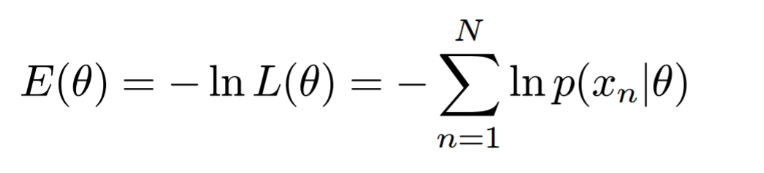
이걸 어찌저찌 전개하면 maximum likelihood parameter? 라는것도 구할 수 있다는데 이건 도저히 모르겠어서 안쓸랜다.

---

아무튼 다시 본론으로 돌아와보겠다.

cost function을 maximum likelihood의 관점에서 작성하는 것은 cost function을 각각 model마다 design 하는 부담을 덜어준다.

activation function이나 뭐 기타등등 연산과정에서 saturate 문제가 생길 수 있는데 negative log-likelihood가 이런 문제들을 피할 수 있게끔 만들어준다고 한다.

정규화(Regularization) 관련해서는 Chapter 7에서 더 자세히 다룬다고 한다.

6.2.1.2 Learning Conditional Statistics

Cost function은 다른 function보다 더 기능적임.

minimizing the MSE(Mean squred error) : input x로부터 output y 예측에 도움 준다.

MSE가 늘 좋은 결과를 주는건 아니라, MAE(Mean absolute error)라던가 RMSE(Root mean squred error)같은 것들도 만들어져 있다. 다들 손실함수의 값을 더 효율적으로 바라보기 위해 만들어진 도구들임.

6.2.2 Output Units

Cost function 고르는 것 ~= Output unit 고르기

6.2.2.1 Linear Units for Gaussian Output Distribution

linear units라고 no nonlinearity 성질 가진 output unit들이 있다. 예를 들면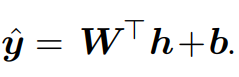이런 거.(W == weight, h == gained inputs, b == bias)

Maximizing the log likelihood == minimizing the mean squred error.

6.2.2.2 Sigmoid Units for Bernoulli Output Distributions

Yes or No로 답해야 하는 문제들이 있다. (이것은 개인가, 고양이인가 등등) - predicting binary variable y.

이러한 binary classification에 대한 maximum-likelihood의 접근은 주로 Bernoulli distribution을 정의하는 것이다.

주로 binary classification에서는 sigmoid unit 사용, sigmoid 학습에는 maximum-likelihood 기법이 사용됨.

sigmoid는 양 끝으로 가면 saturate 되어버림.

sigmoid에서 log(maximizing likelihood) 쓰는 이유는 확률 차이 강조(0~1 값), 계산 안전성을 높이기 위함(로그씌우면 곱셈 형태를 덧셈으로 연산가능)

6.2.2.3 Softmax Units for Multinoulli Output Distribution

n개의 values를 예측할때는 Softmax를 쓴다.

Softmax는 sigmoid의 generalized version이라고 보면 됨.

Softmax도 양 끝으로 가면 saturate 되어버린다. 그래서 약간의 보정 느낌으로 softmax(z) = softmax(z - max(zi)) 형태로 보정해줄 수도 있다.
보통 Output layer에서 많이 쓰지만 필요하면 용도에 따라 internal layer에서도 사용 가능

Softmax도 maximizing log-likelihood에서 효과가 좋음.

Softmax는 argmax function과 더 관련있다. (y값을 최대로 만든 x값을 찾는 함수)

사실 이 다음에도 더 많은 내용들이 있지만 아직 배우지 않은 수학적 용어, 내용들이 이해가 잘 안돼서 넘어갑니다..

아,.... 여기까지 읽고나서 정신이 혼미했

6.3 Hidden Units

어떤 Hidden Unit 쓸지 모르겠으면 국밥 ReLU를 쓰자는 내용이 있었다.

사실 neural network에서 어떤 hidden unit이 제일 output이 잘 나올지 예측하는건 매우 불가능한 일이라.. 진짜 웬만하면 ReLU가 좋음. (원서에서도 ReLU가 default라고 할 정도)

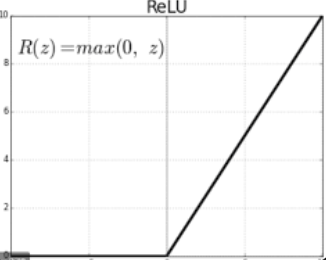
근데 몇몇 hidden Unit들이 미분불가능점이 있음. 당장 ReLU만 봐도 함수가 g(z) = max{0, z} 라서 z = 0에서 미분 불가능이라.. 미분을 활용하는 gradient descendant algorithm을 사용하기에 부적절할 수 있으나, z = 0으로 가는 확률이 매우 낮기도 하고 미분불가능 때문에 안쓰기엔 성능이 너무 좋아서 다들 그냥 쓰자쓰자 하고 쓰는 거라고 함.

6.3.1 Rectified Linear Units and Their Generalizations

ReLU는 linear units와 닮아서 최적화하기 쉽다. 함수가 단순해서 sigmoid나 tanh에 비해 연산도 빠르다. (사실 sigmoid나 tanh도 미분이 간단한 편이지만..)

그런데, ReLU도 단점이 있다. 쉽게 말해 g(z) = max{0, z}에서 z = -1을 예측한 것과 z = -1000을 예측한 것의 예측 정확도는 매우 다르지만 둘다 0이 출력되어버리면 가중치가 제대로 업데이트 되지 않는다. 따라서 이를 조절하기 위해 Leaky ReLU, PReLU(parametric ReLU), RReLU(Randomized Leaky ReLU) 등등의 hidden units를 사용하여 z가 negative일 때를 케어해준다고 한다.

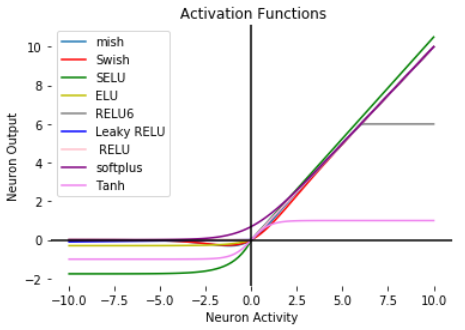
그리고 maxout Units라는 기법도 있다. 여러 선형 함수들 중 최댓값을 갖는 함수를 선택함으로써 치역 값의 증가성을 더 늘리는 것이다. 그러나 이렇게 하면 parameter 수가 늘어서 연산이 좀 더 많아지고, ReLU에 비해 더 많은 Regularization이 필요하다.

장점도 있다. maxout units는 단일 활성화함수와는 다르게 redundancy(전에 했던걸 또 하는)한 경향이 있어 neural networks에서 발생할 수 있는, 전에 배웠던 걸 까먹게 되는, 이른바 catastrophic forgetting 현상을 방지해준다.

6.3.2 Logistic Sigmoid and Hyperbolic Tangent

앞에서 봤던 output sigmoid unit과 유사하게, 전반적인 sigmoidal unit들은 domain 상관없이 saturate 하는 경향이 있다. (함수 생긴 것 부터가 어쩔수 없긴 함)

그리고 non zero-centered issue(x = 0일때 y = 0이 아님)도 있어서 요즘 진짜 안 쓰인다고 한다..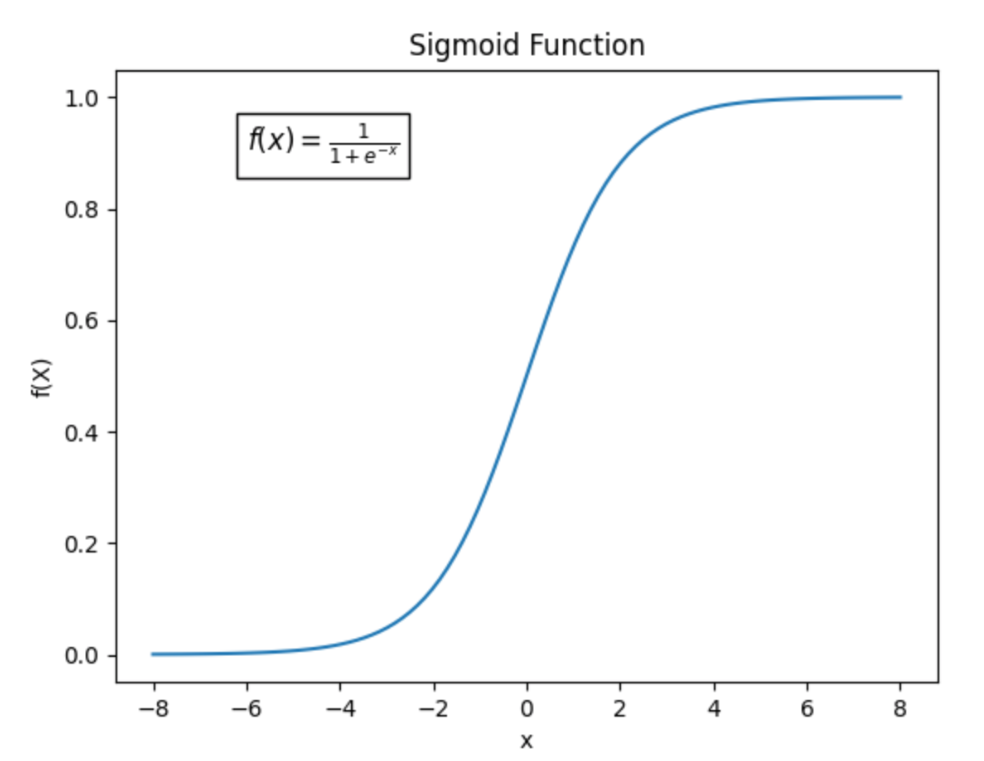

그래서 sigmoidal activation function이 쓰이는 곳에는 hyperbolic tangent activation function이 더 좋은 성능을 보인다고 한다.

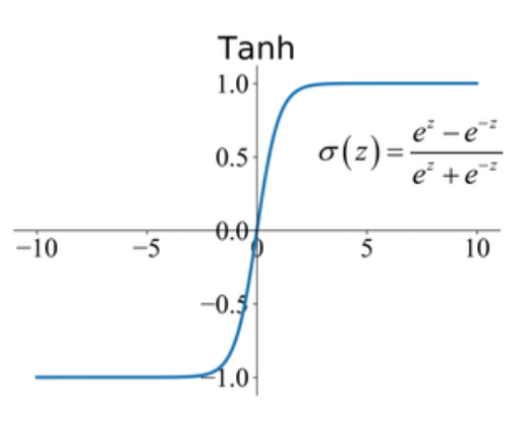
일단 치역이 (0, 1)인 sigmoid에 비해 치역이 (-1, 1)이라 값 표현의 정밀도가 상승했다.

또한 non zero-centered issue도 해결된 모습을 볼 수 있다.

6.3.3 Other Hidden Units

유명한 활성화함수급으로 성능이 준수한 unpublished activation function들이 많다.

신기한 활성화함수 가지고 MNIST같은거 돌려봐도 정확도 차이 1%밖에 안 난다고 한다. 근데 이런거 새로 발견하려면 정확도가 엄청 올라야 나오던지 말던지 하는데 별 차이 없을 거라 연구가 별로 의미 없단다.

neural network에서 모든 layer들이 linear면 neural network 전체가 다 linear가 되어버려서 안되고, 몇몇개는 pure linear layer로 설정하는 정도는 괜찮다.

Linear hidden unit들은 parameters의 수를 잘 줄일 수 있다. (비용 감소)

Softmax는 주로 output layer에서 쓰이는데 필요하면 hidden layer에서 써도 된다.

다른 hidden unit들로는 Radial basis function, RBF unit, Softplus, Hard tanh 등등이 있는데 단점들이 있어서 진짜 잘 안쓰임.

6.4 Architecture Design

Architecture는 overall structure of network를 뜻함.

가장 중요한 architecture 고려사항은 network의 depth 정하는 거랑, each layer의 width 정하기.

network depth 깊으면 generalize 쉽지만 optimize가 어렵다.

적당하게 잘 고르기~~

6.4.1 Universal Approximation Properties and Depth

feedforward networks with hidden layers provide a linear approximation framework.

Universal approximation theorem: nonlinear한 neural network의 크기가 충분히 크고, hidden layer에 any squashing activation function이 있는 경우에는 어떤 함수던지간에 그 함수로 근사할 수 있다.

사실 이것때문에 딥러닝이 뜬거나 마찬가지이다.

greater depth가 결과는 잘 나오는데 해야할 게 많음.

6.4.2 Other Architecture Considerations

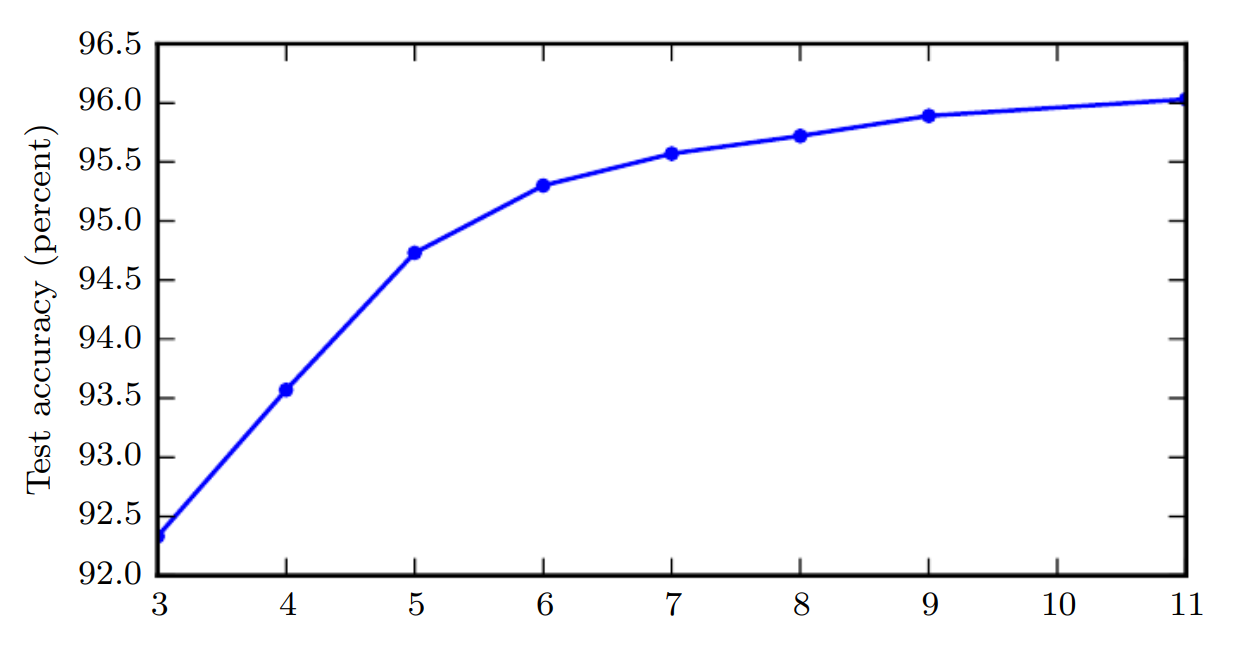
x : network의 depth

depth가 늘어날수록 accuracy가 증가한다.

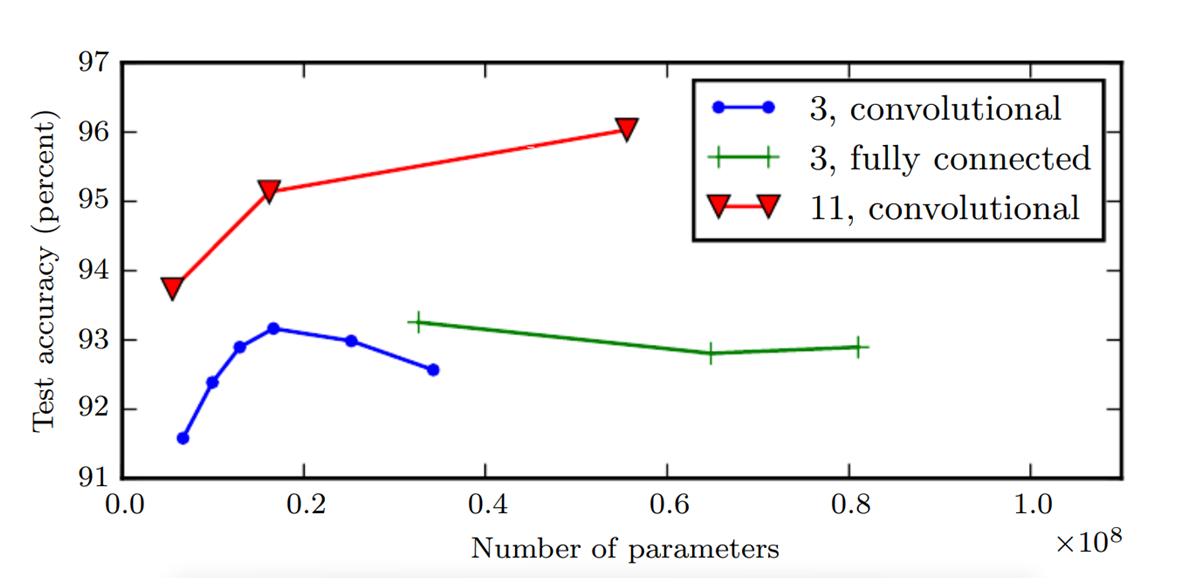
또 다른 중요한 고려사항은, 너무 많은 수의 parameters는 overfitting 문제를 야기한다. 위의 그림에서도 볼 수 있듯, parameter 수가 늘어나면서 accuracy가 낮아지는 지점이 존재한다.

또한 parameter 수가 너무 많으면 연산 시간도 오래 걸린다. 따라서 가중치의 영향을 작게 하거나 필요없는 가중치는 사용하지 않도록 하면서 모델의 효율성을 높인다.

이렇게 경량화를 하는 것은 딥러닝 모델에 있어 매우 중요한 절차로 자리잡았다. (Sparse activation)

6.5 Back-propagation and Other Differentiation Algorithms

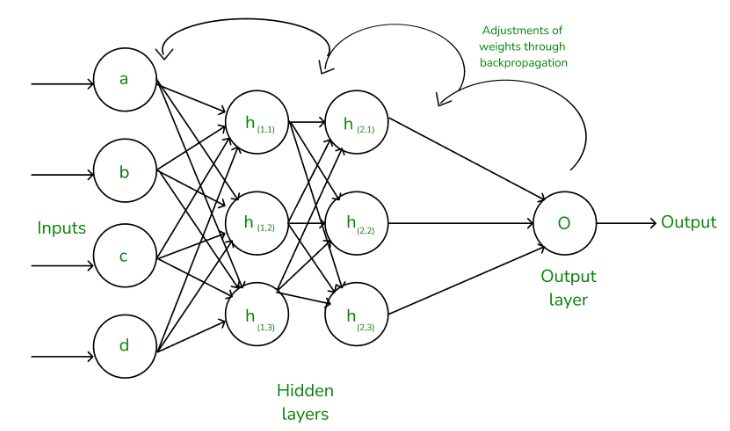
Output layer에서부터 역으로 가중치를 조정하는 학습방법을 Backpropagation, Backprop (simply)이라고 불린다.

Input layer에서부터 모든 가중치 조절해가면서 학습하면 연산량이 말이 안되니까 Output layer에서부터 역으로 바꿔나가는 것.

6.5.1 Computational Graphs

대충 이 책에서는 graph의 node가 variable (some scalar, vector, matrix, tensor) 나타낸다는 내용.

그리고 operation이라는 개념을 설명했다.

operation: a simple funciton of one or more variables.

6.5.2 Chain Rule of Calculus

Backpropagation에서는 Chain Rule이 쓰인다.

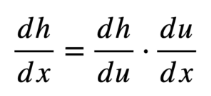
매우 간단한 Chain Rule 예시.

이걸 각 노드들, 가중치들마다 먹이면서 역으로 가는것이다.

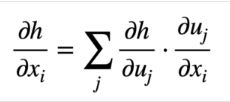
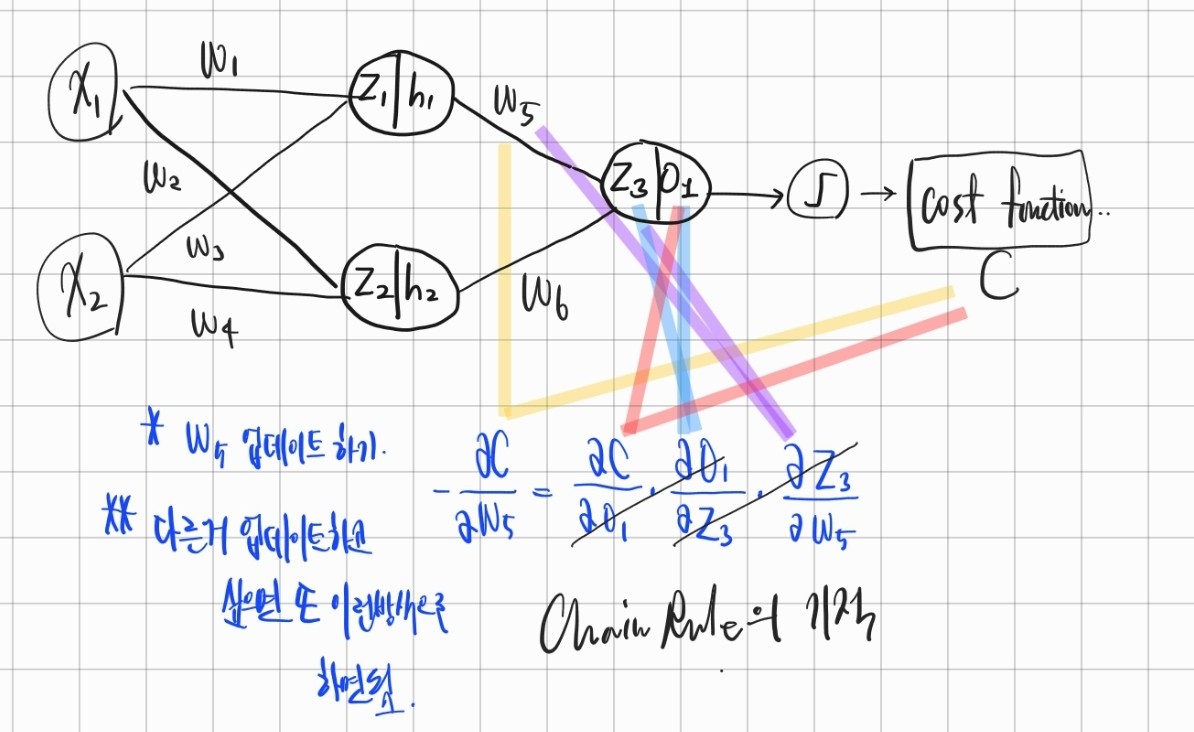
인터넷에 맘에 드는 그림이 없어서 내가 그렸음. 진짜못그렸다

아무튼 체인 룰 계속 먹이면서 가중치 수정하면 됨.

backpropagation은 memory 줄이려고 만들어진 방법임. 각각 node들을 정확하게 한번씩만 방문하니까 좋아요.

사실 backpropagation보다 메모리 덜 쓰는 방법도 있는데, 나중 Chapter에서 알려준다네요.

6.5.4 Back-propagation Computation in Fully-connected MLP

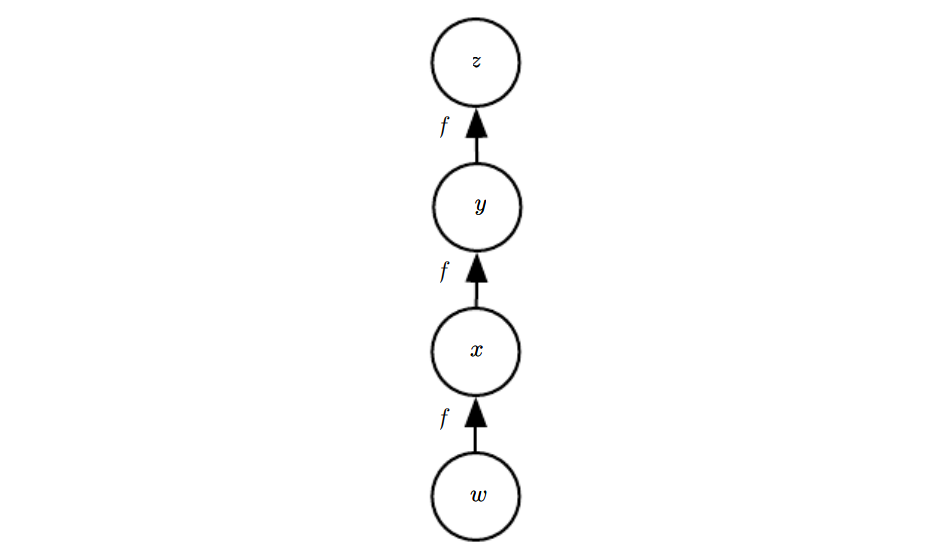
이렇게 생겨먹은 신경망에서 backpropagation한다고 하면

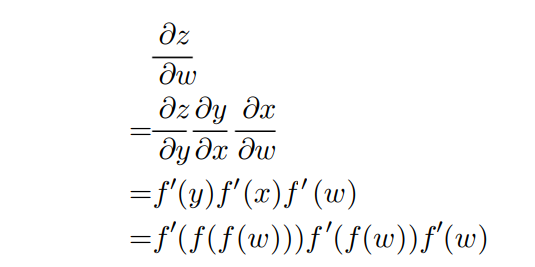
이거 한다는 말임.

참쉽죠잉?

6.5.5 Symbol-to-Symbol Derivatives

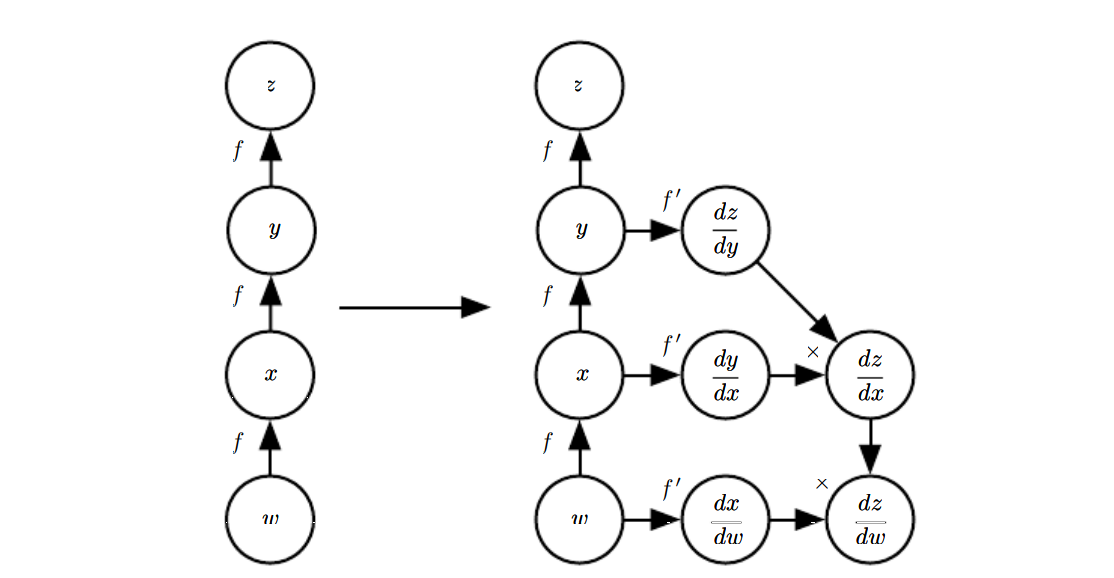
backpropagation을 이렇게도 표현할 수 있네요.

6.5.6 General Back-propagation

V를 tensor, G를 graph라고 할 때,

각각 함수를 정의한다고 칩시다.

get_operation(V): returns the operation that computes V.

get_consumers(V): returns the list of variables that are children of V in the computational graph G.

get_inputs(V, G): returns the list of variables that are parents of V in the computational graph G.

op.bprop(inputs, X (gradient we wish to compute), G) must return:

(그냥 Chain Rule)

이런건 pseudo code에서 쓰이는 거니까 엄밀하게 설명은 안할게용.

n개의 node가 있다고 가정할 때, backprop은 한개 가중치 업데이트 할 때 O(n)가 소요된다.

n개의 가중치 다 업데이트 하려면 O(n^2)가 소요된다. (진짜 계산이 단순하다고 했을 때)

backpropagation for n nodes는 table filling같은 느낌이 들지 않나요? 이런 table filling strategy를 dynamic programming이라고도 불립니다.

내가 DP라는 단어를 여기서 보게 되다니..

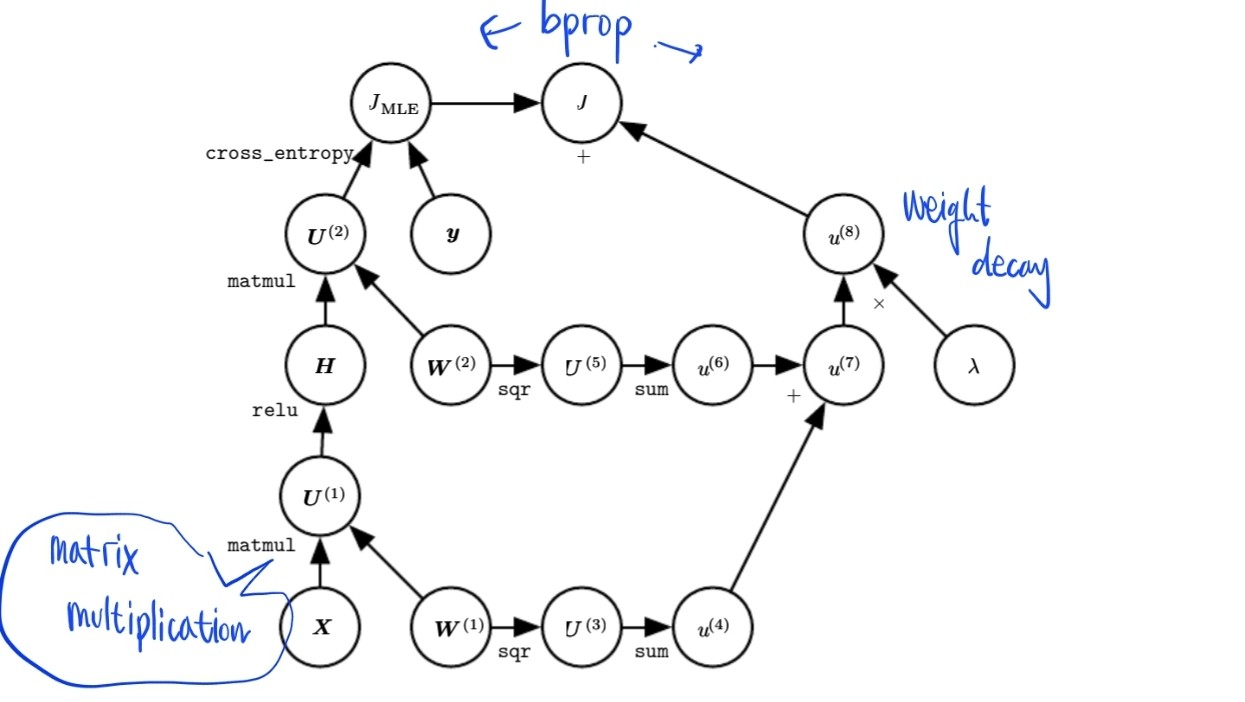
6.5.7 Example: Back-Propagation for MLP Training

간단한 인공신경망으로 학습해봅시다.

이 모델 학습을 위해,

• minibatch stochastic gradient descendant 사용
• backpropagation 사용
• matrix X
• vector class label y
• one hidden layer ReLU H = max{0, XW}
• includes cross-entropy (Minimizing cross-entropy performs maximum likelihood)
• To realistic, also included Regularization term.
  

MLP에서 backpropagation의 연산의 시간 복잡도는 batch size, 순전파 시간, 역전파 시간이 다 포함되기 때문에 bubble sort 알고리즘 같이 딱 잘라서 선언이 불가하다.

6.5.8 Complecations

실제 세상에서 딥러닝 구현하려면 여러가지 데이터 타입도 다 고려해야 해서.. 여러가지를 더 신경 써야 한다.

6.6 Historical Notes

초기 모델은 linear model이었다.

dynamic programming에 기반한 MLP 학습은 1960s ~ 1970s에 만들어짐.

가장 큰 neural network의 성장은 다음 두 가지이다.

• 더 커진 datasets이 neural network의 통계적 일반화 부담을 줄여줬다.
• mean squred error를 cross-entropy 기반 cost function들로 바꾼 게 더 좋은 performance의 향상을 보여줬다.

그리고 ReLU는 사람들이 처음에 맘에 안들어서 안쓰다가 요즘은 너도나도 쓰는중

The half-rectifying nonlinearity(Sparse activation)는 다음의 biological neurons의 장점들을 따라하려고 만들어졌다.

• For some inputs, some neurons are inactive.
• for some inputs, a biological neuron's output is a some input of another neuron.
• They should have sparse activations.

예전에는 Support vector machine 많이 쓰다가 요즘은 gradient descendant를 쓰는 추세.

옛날에는 supervised learning이라고 해서 Machine Learning이 주를 이루다가 Deep Learning 넘어와선 unsupervised Learning trend 정착.

끝!

설마 여기까지 읽은사람 없겠지? 있다면 감사하고요
그냥 제가 나중에 보려고 써놓은것도 있고 기록좀 남겨보고 싶었어요. 첫 글이라 부족하지만 봐주셔서 감사합니다.