[강화학습] Dueling DQN

Dueling DQN이란 신경망이 근사하는 목표인 $Q(s,a)$가 상태의 가치와 행동의 이득으로 나누어 질 수 있다는 사실에 근거하여 기본 DQN을 개선한 모델입니다.

$Q(s,a)=V(s)+A(s,a)$

• Q(s,a): 상태-행동 가치 함수, 상태 $s$에서 행동 $a$을 하였을 때 얻을 수 있는 이득
• A(s,a): 상태 $s$에서 행동의 이득
• V(s): 상태 가치 함수, 상태 $s$에서 최적으로 행동하였을 때, 얻을 수 있는 할인된 총 보상에 대한 기댓값
  $V(s)=\displaystyle\max_aQ(s,a)=Q(s,a^*)$

위의 식을 다시 이해해보면 행동 이득 $A(s,a)$는 상태 가치$V(s)$와
기존 신경망의 구조에서 상태의 가치와 행동의 이득을 명확히 구분함으로써 더 나은 학습 안정성, 빠른 수렴성, 더 좋은 성능을 보여줄 수 있게 되었습니다.

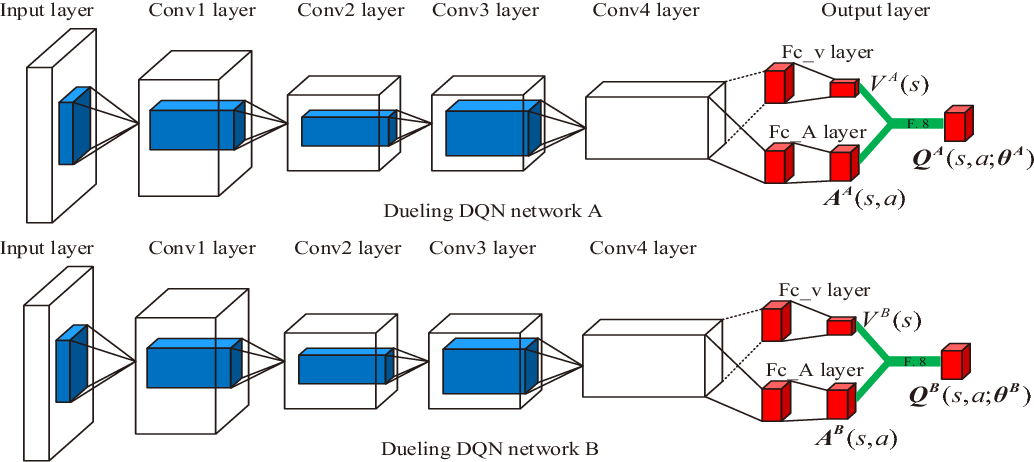
위 그림의 하단 신경망과 같이 상태가치와 행동이득을 컨볼루션 계층 후에 독립적인 경로를 통해 각각 예측하고 마지막에 모두 더하여 $Q(s,a)$를 얻습니다.

이득은 어떤 행동은 평균보다 나쁘고, 어떤 행동은 평균보다 좋다는 것을 나타내기 때문에, 모두 양수이거나 모두 음수인 경우는 존재하면 안됩니다. 즉 이득의 평균값이 0이 되어야 합니다.
나쁜 예: $V(s)=0\,\,\,\,\,, A(s)=[\quad\;\;1,\quad\;\,2,\;\;\,3,\;\;\;4]$
좋은 예: $V(s)=2.5, A(s)=[-1.5, -0.5, 0.5, 1.5]$

이 제약 조건을 강제하는 가장 쉬운 방법은 dueling network가 소개된 논문에서 사용한 다음과 같이 Q표현식에서 이득의 평균을 뺀 값을 사용하는 방법입니다.