Gym Acrobot-v1

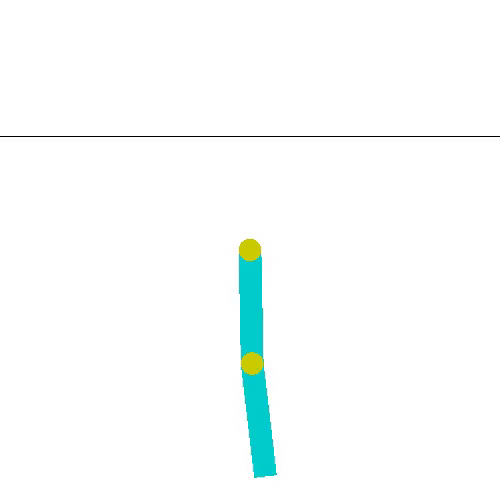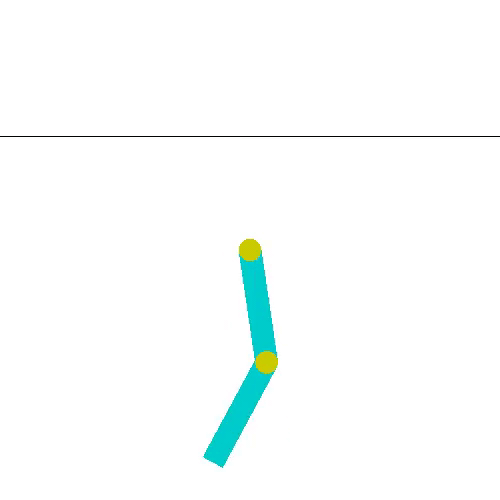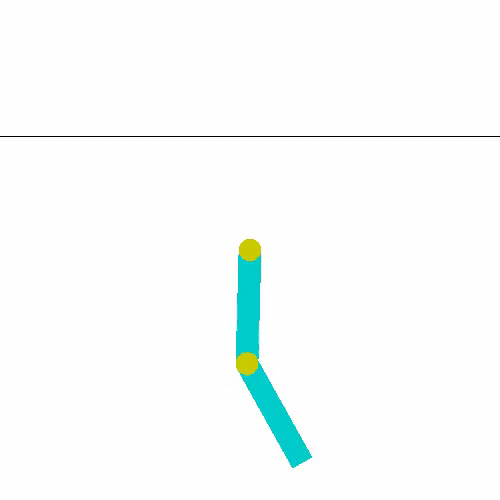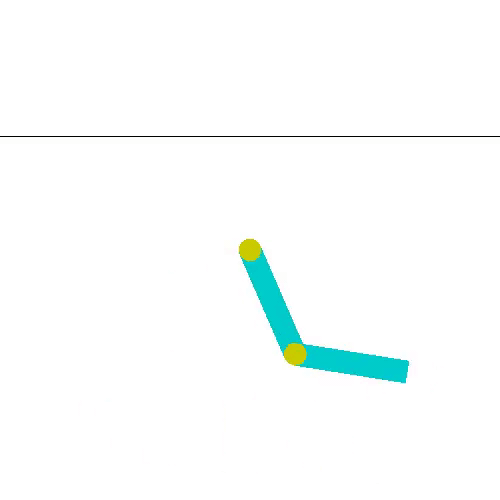
이 포스트에서는 OpenAi의 Gym에서 제공하는 Acrobot-v1 환경이 어떻게 정의 되어 있는지 분석합니다.
하나하나 뜯어보며 분석하고 나면 이 라이브러리를 기반으로 나만의 환경을 만들 수 있습니다.

---

Link

환경이 기구학적으로 어떻게 정의 되어 있는지 살펴보면 다음과 같이 정리할 수 있습니다.

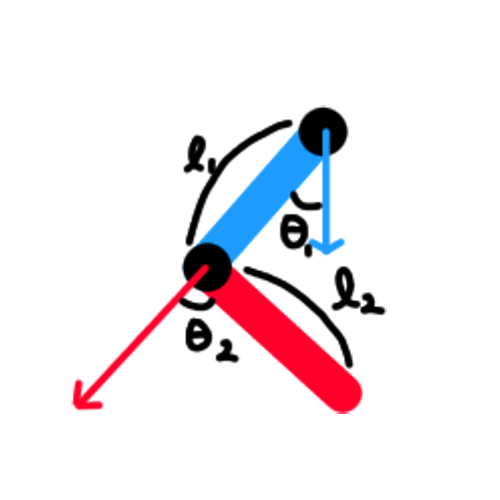
두 링크는 엇갈리게 설계되어 있어 만약 서로 겹쳐도 부딪히지 않는다는 가정이 있습니다.
가장 중심점을 base joint라고 한다면 각 링크는 base joint로부터 순서대로 link1, link2로 정의됩니다.
링크1의 시초선은 하단방향(중력방향)이고, 링크2의 시초선은 1번 링크 방향입니다.
즉 링크2 각도는 링크1에 대한 상대적인 각도입니다.

---

Constant Definition

gym 라이브러리 내부에 선언되어 있는 상수값입니다.

constant	value	unit
INK_LENGTH_1	1.0	[m]
LINK_LENGTH_2	1.0	[m]
LINK_MASS_1	1.0	[kg] mass of link 1
LINK_MASS_2	1.0	[kg] mass of link 2
LINK_COM_POS_1	0.5	[m] position of the center of mass of link 1
LINK_COM_POS_2	0.5	[m] position of the center of mass of link 2
LINK_MOI	1.0	moments of inertia for both links
MAX_VEL_1	4 * pi	[rad/sec]
MAX_VEL_2	9 * pi	[rad/sec]

---

Observation Space

관측값에서 0번과 1번은 1번 링크 각도의 삼각함수 값, 2번과 3번은 2번 링크 각도의 삼각함수 값입니다.
4번과 5번은 각 링크의 각속도를 나타내고 있습니다.

코드상에서 Observation space는 Box Class로 표현합니다.

0	1	2	3	4	5
$\cos(\theta_1)$	$\sin(\theta_1)$	$\cos(\theta_2)$	$\sin(\theta_2)$	$\quad\dot\theta_1\quad$	$\quad\dot\theta_2\quad$

---

Action Space

행동은 총 3가지이고, 링크1과 링크2를 연결하는 joint의 토크를 의미합니다.

코드상에서 Observation space는 Discrete Class로 표현합니다.

Action	0	1	2
Torque	-1	0	1

---

Initial Value

환경을 초기화 시키는 environment의 reset함수의 정의는 다음과 같습니다.

def reset(self):
    self.state = self.np_random.uniform(low=-0.1, high=0.1, size=(4,))
    return self._get_ob()

리셋을 하는 경우 초깃값은 -0.1에서 0.1사이의 균등분포 난수로 결정됩니다.
따라서 $\pm3\degree$의 각도와 $\pm0.1N\cdot m$의 토크를 갖게 됩니다.

아래의 표는 100,000번 반복하였을 때 초기값의 최대, 최솟값입니다.

index	0	1	2	3	4	5
meaning	$\cos(\theta_1)$	$\sin(\theta_1)$	$\cos(\theta_2)$	$\sin(\theta_2)$	$\quad\dot\theta_1\quad$	$\quad\dot\theta_2\quad$
MAX	1.	0.09983311	1.	0.09983235	0.09999991	0.09999979
MIN	0.9950042	-0.09983071	0.99500427	-0.09983242	-0.09999971	-0.09999975

---

Terminal Condition

라이브러리에서 제시하는 terminal contidion은 다음과 같습니다.

def _terminal(self):
    s = self.state
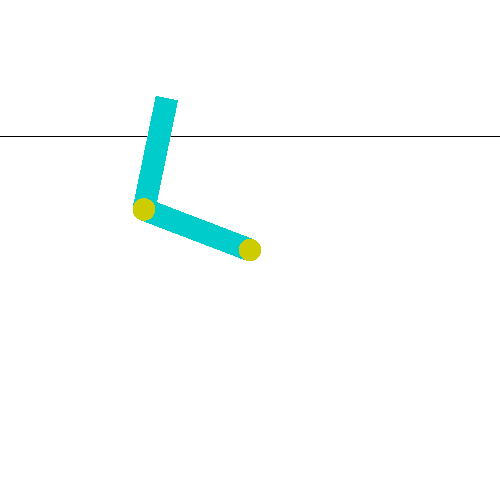
    return bool(-cos(s[0]) - cos(s[1] + s[0]) > 1.)

이는 다음과 같이, 상단에 직선으로 표시 된 영역을 어느 정도 넘겼다는 의미입니다.

---

Analysis

역학에 대한 해석은 4차 runge-kutta법을 사용합니다.
아래는 gym 라이브러리 내의 rk4 함수입니다.

def rk4(derivs, y0, t, *args, **kwargs):
    try:
        Ny = len(y0)
    except TypeError:
        yout = np.zeros((len(t),), np.float_)
    else:
        yout = np.zeros((len(t), Ny), np.float_)

    yout[0] = y0


    for i in np.arange(len(t) - 1):

        thist = t[i]
        dt = t[i + 1] - thist
        dt2 = dt / 2.0
        y0 = yout[i]

        k1 = np.asarray(derivs(y0, thist, *args, **kwargs))
        k2 = np.asarray(derivs(y0 + dt2 * k1, thist + dt2, *args, **kwargs))
        k3 = np.asarray(derivs(y0 + dt2 * k2, thist + dt2, *args, **kwargs))
        k4 = np.asarray(derivs(y0 + dt * k3, thist + dt, *args, **kwargs))
        yout[i + 1] = y0 + dt / 6.0 * (k1 + 2 * k2 + 2 * k3 + k4)
    return yout

---