[강화학습] A2C

Eugene CHOI·2021년 5월 12일

Actor-Critic a2c adventage 강화학습

Machine Learning

목록 보기

10/13

Variance

앞선 포스트에서 설명한 바와 같이 분산을 줄이는 것은 성능 향상에 꽤 큰 기여를 할 수 있습니다.

분산이 무엇인지, 어떤 성질을 가지는지부터 알아보겠습니다.
variance의 정의는 다음과 같습니다.

\begin{aligned} V[X] &= E[(X-\mu)^2]\\ &=E[X^2]-E[X]^2\\\,\\ V[X]&=\frac{\sum(x_i-\bar x)^2}{n}\end{aligned}

다음과 같이 평균이 0인 5개의 데이터가 있다고 합시다.

X	-2	-1	0	1	2
$(x_i-\bar x)^2$	4	1	0	1	4

이 데이터의 분산은 $\frac{4+1+0+1+4}{5}=2$ 입니다.

만약 모든 데이터에 2를 더한다고 하면 다음과 같이 바뀌게 될 것입니다.

X	0	1	2	3	4
$(x_i-\bar x)^2$	4	1	0	1	4

이 데이터의 분산은 여전히 $\frac{4+1+0+1+4}{5}=2$ 입니다.

이와 같이 분산의 특성 중 하나는 모든 데이터에 같은 값을 더하거나 빼도 변하지 않는다는 것입니다.

V[X - b] = V[X]

이번에는 모든 값에 2를 곱해보겠습니다.

X	0	2	4	6	8
$(x_i-\bar x)^2$	16	4	0	4	16

이 데이터의 분산은 전과 다르게 $\frac{16+4+0+4+16}{5}=2*2^2=8$ 입니다.
따라서 다음과 같이 정의할 수 있습니다.

V[aX] = a^2V[X]

Baseline

이와 같이 어떤 값을 더하는 것 자체는 분산이 바뀌지 않지만, 곱해져 있는 어떤 값을 가산하는 것은 분산에 영향을 끼치게 됩니다.
PG 목표함수를 다시 살펴봅시다.

\triangledown_\theta J(\theta) \approx E_{\pi_\theta}[Q(s,a)\triangledown_\theta \log\pi(a|s)]

목표함수의 분산은 $V[aX]$ 와 같은 형태임을 알 수 있습니다.
그래서 $Q(s,a)$ 에 어떤 값을 빼 주게 되면 분산이 줄어드는 효과를 볼 수 있습니다.
A2C 알고리즘에서 이 어떤 값을 baseline이라고 하기로 하였습니다.

Entropy

지난 포스트에서 다루었던 REINFORCE의 목표함수를 다시 복습해보겠습니다.
엔트로피( $H$ )는 어떤 시스템의 불확실성을 측정하는 척도입니다. 정책의 엔트로피는 에이전트가 수행할 행동에 대해 얼마나 불확실한지를 보여줍니다.
손실 함수에서 이 엔트로피를 빼 줌으로써 다음 취할 행동에 대하여 너무 확신하고 있는 에이전트에게 벌을 주어 local minimum에 빠지지 않게 탐색을 계속 시킬 수 있었습니다.

H(\pi)=-\sum\pi(a|s)\log\pi(a|s)

Advantage

A2C은 Dueling DQN에서 배웠던, 상태-행동 가치 함수가 상태 가치 함수와 행동 이득으로 나뉠 수 있다는 이론에 기초하여 baseline을 사용하는 알고리즘입니다.

$Q(s,a)=V(s)+A(s,a)$

$Q(s,a)$ : 상태-행동 가치 함수, 상태 $s$ 에서 행동 $a$ 을 하였을 때 얻을 수 있는 이득

$A(s,a)$ : 상태 $s$ 에서 행동의 이득

$V(s)$ : 상태 가치 함수, 상태 $s$ 에서 최적으로 행동하였을 때, 얻을 수 있는 할인된 총 보상에 대한 기댓값

위 식은 Dueling DQN을 다룰 때 사용하였던 식과 완전 동일합니다.

위의 식을 baseline으로 쓰기 위해 정리해보면 행동 이득은 다음과 같이 표현됩니다.

A(s,a)=Q(s,a)-V(s)

그래서 기존의 PG식을 다음과 같이 바꾸면 완벽한 baseline이 적용됩니다.

\begin{aligned} &\triangledown_\theta J(\theta) \approx E_{\pi_\theta}[Q(s,a)\triangledown_\theta \log\pi(a|s)]\\ \\ =>\triangledown_\theta J(\theta) &\approx [(Q(s,a)-V(s))\triangledown_\theta \log\pi(a|s)]\\ &\approx E_{\pi_\theta}[A(s,a)\triangledown_\theta \log\pi(a|s)]\end{aligned}

실제 학습 시 문제점은 총 할인 보상 $Q(s,a)$ 에서 빼야 할 상태값 $V(s)$ 가 얼마인지 알 수 없다는 것입니다.
그래서 전문가들은 아래 그림과 같이 $V(s)$ 를 근사하는 또 하나의 신경망을 만들어 이 문제를 해결하였습니다.

A2C Network

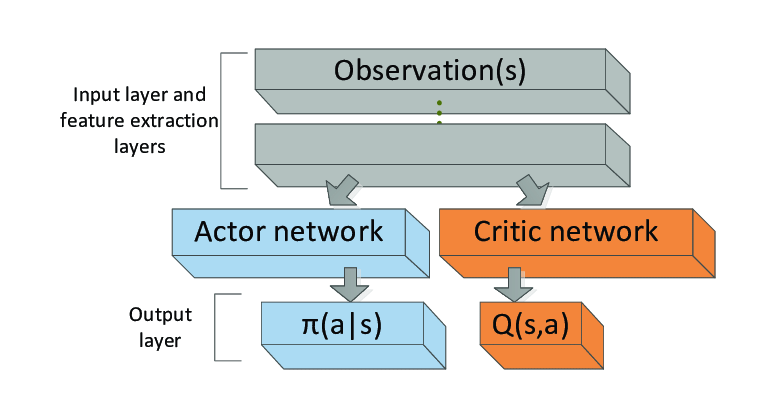
각 행동 확률을 반환하는 신경망(정책망)과 현재 상태에서 얻을 수 있는 미래의 가치(상태 가치)를 반환하는 신경망(가치망)은 개념적으로 별개의 신경망이지만, 실제로 학습할 때는 학습의 효율성 및 수렴성을 고려하여 한 신경망에서 분기되는 형태로 만듭니다.
따라서 A2C 알고리즘은 한 입력층을 가지고, 은닉층에서 확률 분포를 반환하는 정책망과 상태의 가치를 반환하는 가치망으로 분기하여 각각 판단하게됩니다.
이와 같이 두 역할이 분리되어 있기 때문에 Advantage Actor Critic(A2C) 알고리즘이라고 합니다.
정책망은 확률 분포를 반환하기 때문에 보통 sigmoid 활성화 함수를 거쳐 출력됩니다. 가치망의 경우 ReLU 활성화 함수를 거칩니다.

Actor(정책망): 각 행동에 대한 확률 분포( $\pi(a|s)$ )를 반환. 정책망이 어떤 행동을 취해야할지 알려줌.

Critic(가치망): 상태의 가치( $V(s)$ )를 반환, 에이전트의 행동이 예상보다 얼마나 좋을지를 평가.

Loss Function

이 A2C는 신경망에서 보이듯이 정책반복 알고리즘과 가치반복 알고리즘을 조합하여 중간쯤에 있는 알고리즘입니다.
최종적으로 정책망의 gradient loss는 다음과 같습니다.

L_\pi = -\frac 1n\displaystyle\sum_{i=0}^n[(Q(s_i,a_i)-V(s_i)) \log\pi(a_i|s_i)]

$E[X]$ : X에 대한 기댓값

$\log(\pi_\theta(a|s))$ : 상태 s에서 행동 a를 취할 확률의 로그값

$Q_\pi(s,a)-V_{\pi,s}$ : 액션 어드벤티지 $A(s)$ 를 의미

가치망은 Critic이 예측한 미래에 대한 기댓값과 실제 보상의 차이를 loss로 사용합니다. 프레임워크를 사용하여 프로그래밍 시 유의할 점은 모델이 그래프 구조를 가지기 때문에 가치망의 loss를 계산할 시에 정책망으로까지 그라디언트가 전파되지 않도록 설계 하여야 합니다.
가치망의 gradient loss는 다음과 같습니다.