Entropy

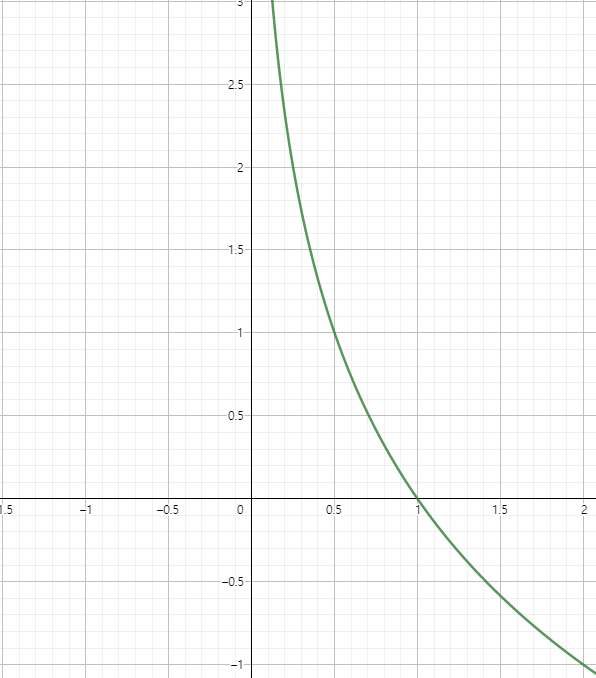
높은 확률로 일어나는 사건은 별로 놀랍지 않습니다. 예를 들어 해가 동쪽에서 뜰 확률은 거의 100% 이기 때문에 이런 확률은 정보의 양이 적습니다.
그래서 얼마나 놀라운지(불확실한지)를 수치적으로 표현할 수 있는 것이 엔트로피 함수 입니다.
엔트로피 식에서 $p(x)$가 작아질 수록$-\log p(x)$는 커지기 때문에 확률이 커질수록 얻는 정보의 양은 줄어든다고 해석할 수 있습니다.

Cross-Entropy

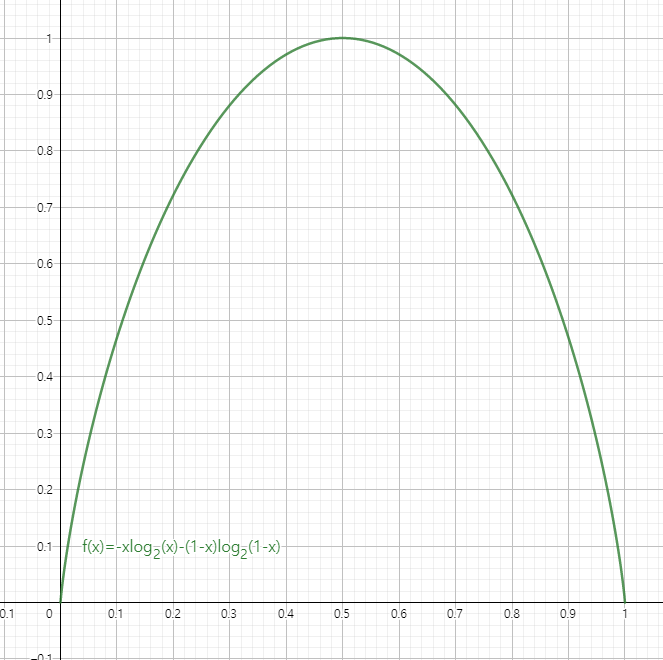
실제 분포 확률인 $p(x)$를 알 수 없을 때, 모델링을 하여 $p(x)$를 예측해보자는 아이디어에서 나온 식입니다. $q(x)$가 모델링을 통해서 구해진 분포 확률입니다.

Calculate Parameters

• $O$: size of output image
• $I$ : size of input image
• $K$: size of kernels used in the Conv layer
• $N$: Number of kernels
• $S$ : Stride of the convolution operation
• $P$ : size of padding

입력 이미지의 사이즈에서 커널 사이즈만큼이 빠지게 됩니다.
패딩을 추가하면 이미지의 상하좌우로 패딩 사이즈만큼 커지게 되므로 가로(세로)쪽만 보면 패딩 사이즈에서 2배가 늘어난 셈이 됩니다.
스트라이드 만큼 건너뛰기를 하기 때문에 이미지는 스트라이드의 배수로 작아집니다.

마지막 Fully Connected(Dense) Layer의 Input size는 다음과 같습니다.

• $I_{dense}$: size of input image of dense layer
• $C_{cnn}$: size of channels
• $W$: length of width
• $H$: length of height
  $I_{dense} = C_{cnn}* W * H$

행렬 $\begin{bmatrix} 1&0&2\\ -1&1&1\\ 2&2&1 \end{bmatrix}$에 필터 $\begin{bmatrix} 1&2\\ 2&1 \end{bmatrix}$를 적용하면 결과는 다음과 같습니다.
편향을 사용하는 경우 출력값의 모든 성분에 편향($b$)를 더해서 출렵합니다.