이번 튜토리얼에서는, 결측값에 대해 어떻게 처리하는지 세 가지 방법에 대해 알아볼 것입니다. 그런 다음 실제 데이터 셋에서 이러한 접근 방식의 효과를 비교합니다.
Introduction
데이터가 결측값으로 끝나는 경우는 다양합니다. 예를 들어서:
- 2개의 침실이 포함된 주택의 경우 세 번째 침실의 크기 값이 존재하지 않음
- 설문 응답자가 자신의 소득을 공유하지 않을 수도 있음
대부분의 머신러닝 라이브러리(scikit-learn 포함)는 모델을 생성할 때 결측값이 있는 데이터를 사용하려도 시도하는 경우 에러를 발생합니다. 따라서, 여러분들은 다음 몇 가지 전략들을 시도할 수 있습니다.
Three Approaches
1) A Simple Option: Drop Columns with Missign Values
가장 간단한 방법은 결측값을 가지고 있는 열을 없애는 것입니다.
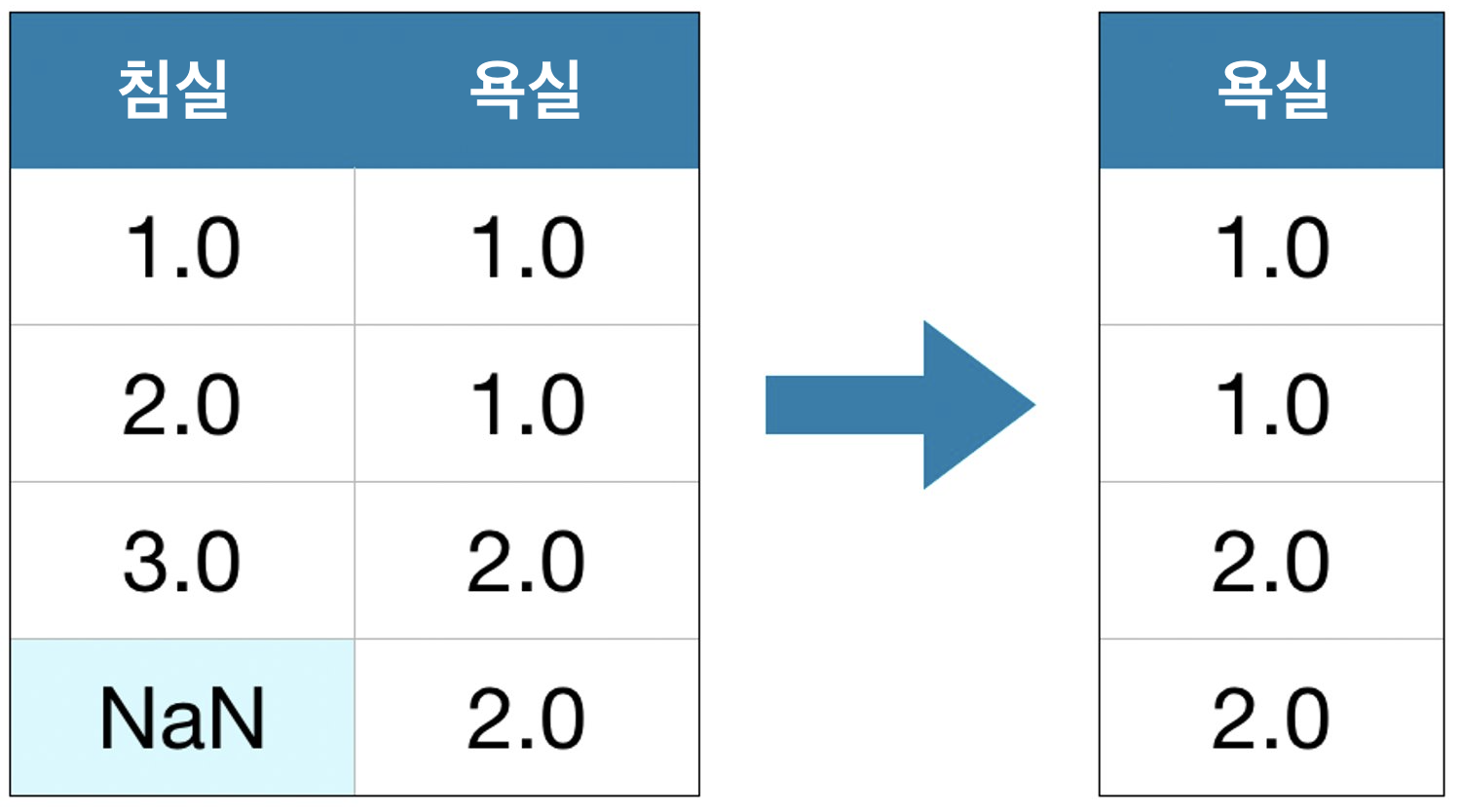
드롭된 열의 대부분이 값이 누락되지 않는 한 이 방법을 사용하면 모델에서 많은 (유용할 수 있는) 정보에 접근할 수 없게 됩니다. 극단적인 예로 10,000개의 행이 있는 데이터셋에서 중요한 열 하나에 항목 하나가 누락되어 있다고 가정해 보세요. 이 방법을 사용하면 해당 열이 완전히 삭제됩니다!
2) A Better Option: Imputation
Imputation(대체) 은 결측값을 일부 숫자로 채웁니다. 예를 들어, 각 열에서의 평균 값으로 채울 수 있습니다.
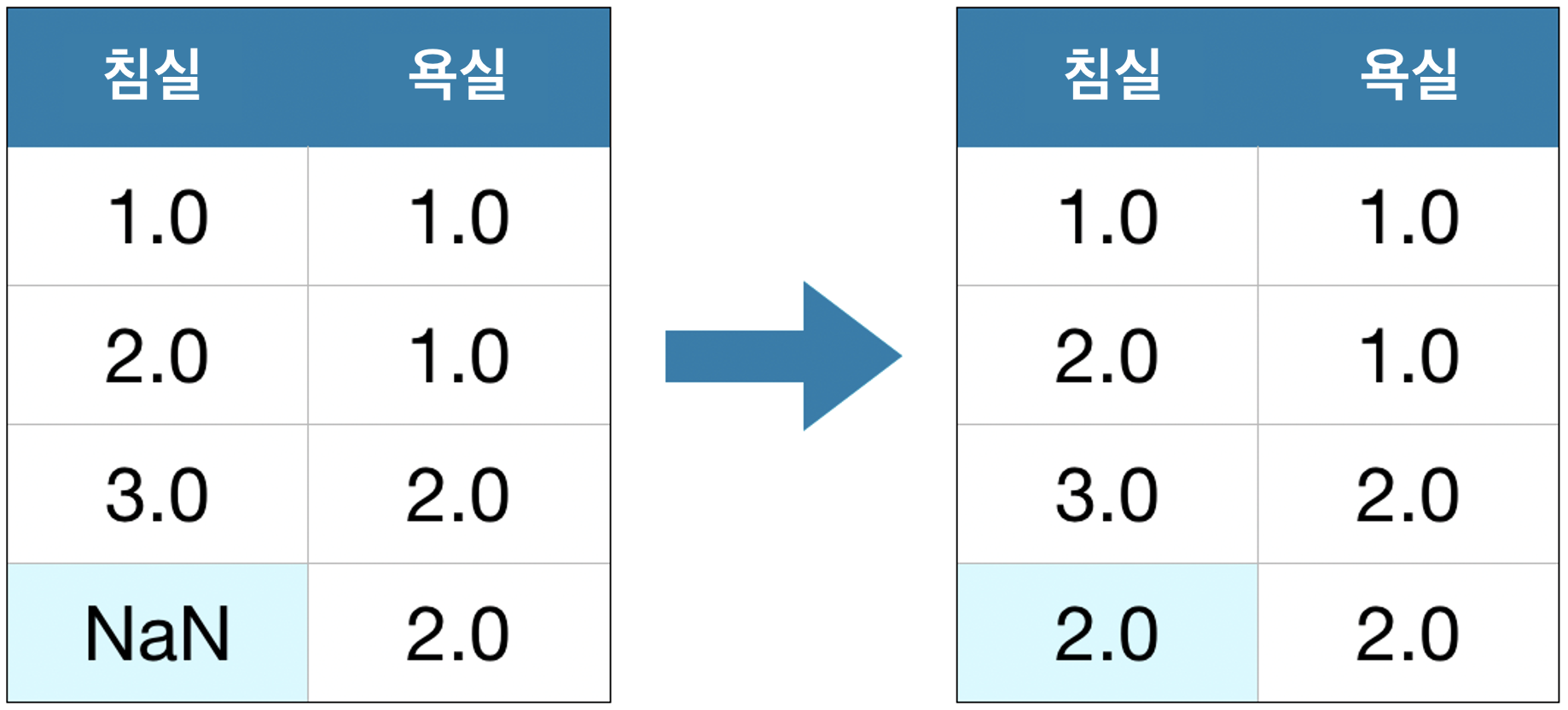
대부분의 경우 대체 값이 정확하지는 않지만, 일반적으로 열을 전체적으로 드롭하여 얻을 수 있는 모델보다 더 정확한 모델을 얻을 수 있습니다.
3) An Extension to Imputation
대체는 표준적인 접근법이고, 보통의 경우 잘 작동합니다. 그러나 대체된 값은 실제 값보다 체계적으로 높거나 낮을 수 있습니다(데이터셋에서 수집되지 않음). 또는 결측값이 있는 행은 다른 방식으로 고유한 값을 가질 수 있습니다. 이 경우 모델에서 원래 결측값을 고려하여 더 나은 예측을 할 수 있습니다.
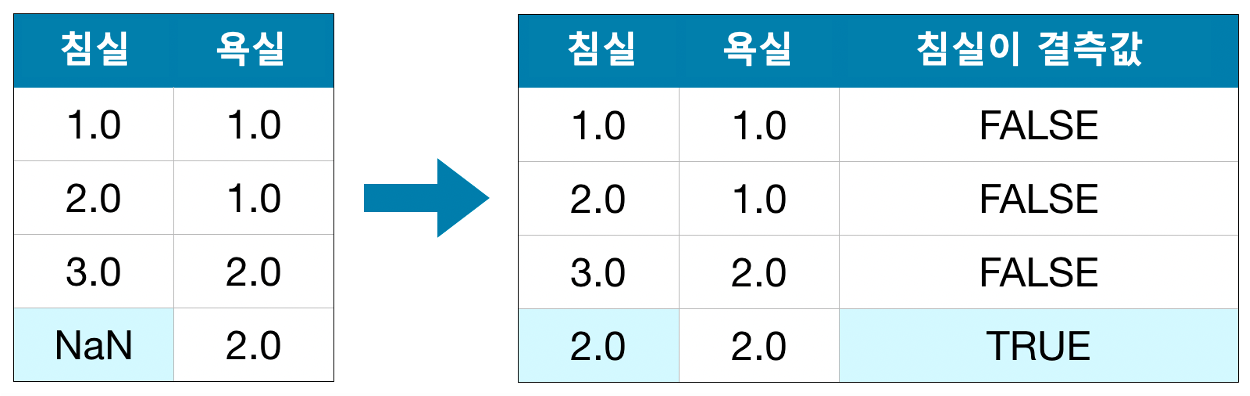
이 접근 방식에서는 2)와 같이 결측값을 대체합니다. 또한 원래 데이터셋에서 누락된 항목이 있는 각 열에 대해 대체된 항목의 위치를 보여주는 새 열을 추가합니다.
경우에 따라 이러한 방식으로 결과가 의미있게 개선될 수 있습니다. 그러나 다른 경우에는 전혀 도움이 되지 않습니다.
Example
이번 예시에서는 멜버른 주택 데이터셋을 사용하여 작업합니다. 우리 모델은 방의 수, 땅의 크기 등과 같은 정보를 활용하여 주택의 가격을 예측할 것입니다.
우리는 데이터 읽기 단계에 초점을 맞추지 않을 것입니다. 대신 학습 및 유효성 검사 데이터로 X_train, X_valid, y_train, y_valid 값이 있는 상황을 가정하고 이어나가겠습니다.
import pandas as pd
from sklearn.model_selection import train_test_split
# 데이터 읽기
data = pd.read_csv('../input/melbourne-housing-snapshot/melb_data.csv')
# 타겟 설정
y = data.Price
# 간단하게 하기 위해서, 숫자 예측 변수만 사용
melb_predictors = data.drop(['Price'], axis=1)
X = melb_predictors.select_dtypes(exclude=['object'])
# 데이터를 훈련/유효성 검사 집합으로 나눔
X_train, X_valid, y_train, y_valid = train_test_split(X, y, train_size=0.8, test_size=0.2,
random_state=0)Define Function to Measure Quality of Each Approach
결측값을 처리하는 다양한 접근 방식을 비교하기 위해 새로운 함수score_dataset()을 정의합니다. 이 함수는 랜덤 포레스트 모델의 MAE(Mean Absolute Error) 값을 리턴합니다.
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_absolute_error
# 여러 접근 방식을 비교하기 위한 함수
def score_dataset(X_train, X_valid, y_train, y_valid):
model = RandomForestRegressor(n_estimators=10, random_state=0)
model.fit(X_train, y_train)
preds = model.predict(X_valid)
return mean_absolute_error(y_valid, preds)Score from Approach 1 (Drop Columns with Missing Values)
학습 및 유효성 검증 데이터를 모두 사용하기 때문에, 두 데이터 프레임에서 동일한 열을 삭제하는 것이 좋습니다.
# 결측값을 가지고 있는 열의 이름 찾기
cols_with_missing = [col for col in X_train.columns
if X_train[col].isnull().any()]
# 훈련 / 유효성 검증 데이터에서 열 제거
reduced_X_train = X_train.drop(cols_with_missing, axis=1)
reduced_X_valid = X_valid.drop(cols_with_missing, axis=1)
print("MAE from Approach 1 (Drop columns with missing values):")
print(score_dataset(reduced_X_train, reduced_X_valid, y_train, y_valid))

Score from Approach 2 (Imputation)
이번에는 SimpleImputer를 사용하여 결측값을 각 열의 평균 값으로 바꿀 것입니다.
이 과정은 단순하지만, 평균 값을 채우는 것은 일반적으로 꽤 잘 수행됩니다(하지만 데이터 집합에 따라 다름). 통계학자들은 대체 값을 결정하는 더 복잡한 방법(예: 회귀 대체)을 테스트했지만, 복잡한 전략은 일반적으로 정교한 머신 러닝 모델에 이점을 제공하지 않습니다.
from sklearn.impute import SimpleImputer
# 대체
my_imputer = SimpleImputer()
imputed_X_train = pd.DataFrame(my_imputer.fit_transform(X_train))
imputed_X_valid = pd.DataFrame(my_imputer.transform(X_valid))
# 대체로 인해 제거된 열 이름 재배치
imputed_X_train.columns = X_train.columns
imputed_X_valid.columns = X_valid.columns
print("MAE from Approach 2 (Imputation):")
print(score_dataset(imputed_X_train, imputed_X_valid, y_train, y_valid))
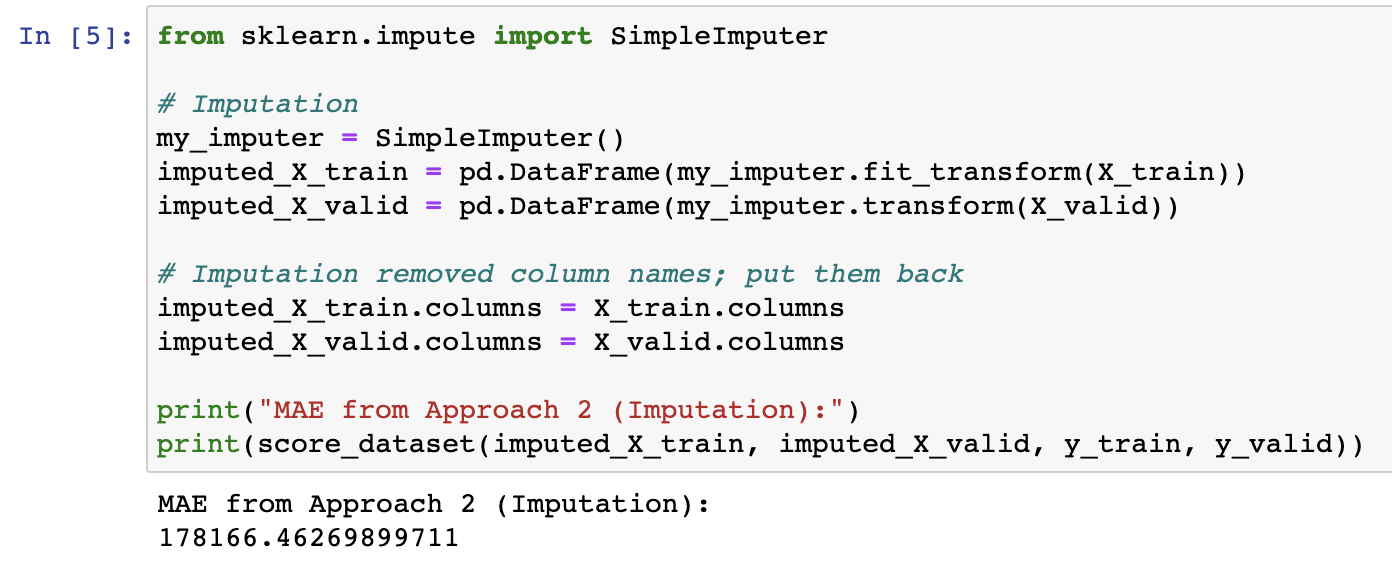
우리는 접근법2의 MAE가 접근법1보다 낮으므로 접근법2가 이 데이터셋에서 더 나은 성는을 나타내는 것을 확인했습니다.
Score from Approach 3 (An Extension to Imputation)
다음으로, 결측값을 대체하며 동시헤 결측값을 추적합니다.
# 값 대체시 원본 데이터의 수정을 방지하기 위해서 복사
X_train_plus = X_train.copy()
X_valid_plus = X_valid.copy()
# 결측값을 나타내는 새로운 열 생성
for col in cols_with_missing:
X_train_plus[col + '_was_missing'] = X_train_plus[col].isnull()
X_valid_plus[co
l + '_was_missing'] = X_valid_plus[col].isnull()
# 대체
my_imputer = SimpleImputer()
imputed_X_train_plus = pd.DataFrame(my_imputer.fit_transform(X_train_plus))
imputed_X_valid_plus = pd.DataFrame(my_imputer.transform(X_valid_plus))
# 대체로 인해 제거된 열 이름 재배치
imputed_X_train_plus.columns = X_train_plus.columns
imputed_X_valid_plus.columns = X_valid_plus.columns
print("MAE from Approach 3 (An Extension to Imputation):")
print(score_dataset(imputed_X_train_plus, imputed_X_valid_plus, y_train, y_valid))

결과에서 볼 수 있는 것 처럼, 접근법3의 결과가 접근법2보다 조금 덜 좋습니다.
So, why did imputation perform better than dropping the columns?
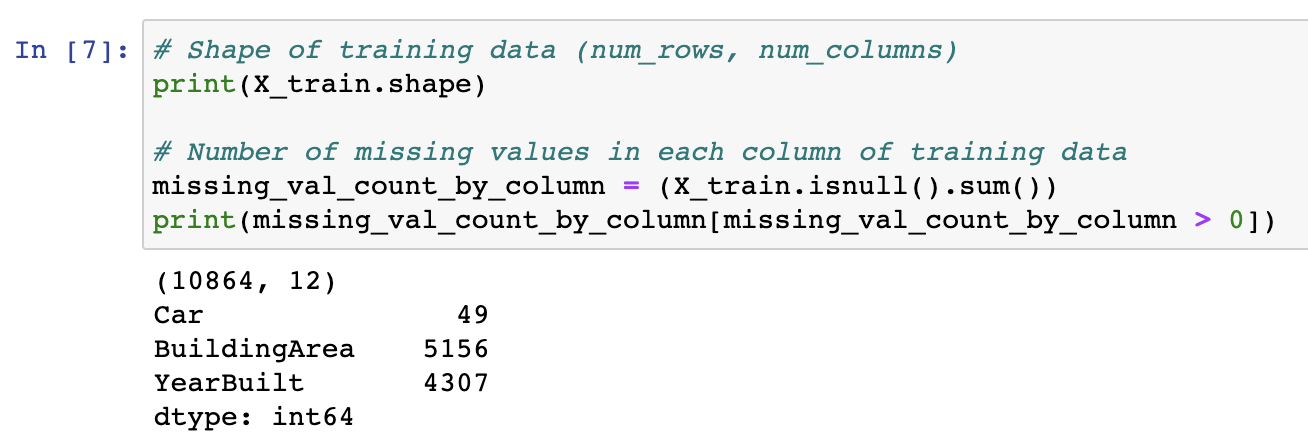
학습 데이터에는 10,864개의 행과 12개의 열이 있으먀, 세 개의 열에 결측값이 포함되어 있습니다. 또한, 각 열에 대해 결측된 항목이 절반 미만입니다. 따라서 열을 삭제하면 많은 유용한 정보가 제거되므로, Imputation 방법이 더 잘 수행될 수 있습니다.
# 학습 데이터의 모양(행 개수, 열 개수)
print(X_train.shape)
# 훈련 데이터 각 열의 결측값 개수
missing_val_count_by_column = (X_train.isnull().sum())
print(missing_val_count_by_column[missing_val_count_by_column > 0])
Conclusion
일반적으로 결측값을 귀속시키는 것(접근법2, 접근법3)은 결측값이 있는 열을 단순히 제거했을 때(접근법2)에 비해 더 나은 결과를 얻을 수 있습니다.
Your Turn
이 예제에서 결측값에 대한 각 접근법에 대한 결과를 비교하세요.
