Reference
- source : 수학으로 풀어보는 강화학습 원리와 알고리즘
Problem
-
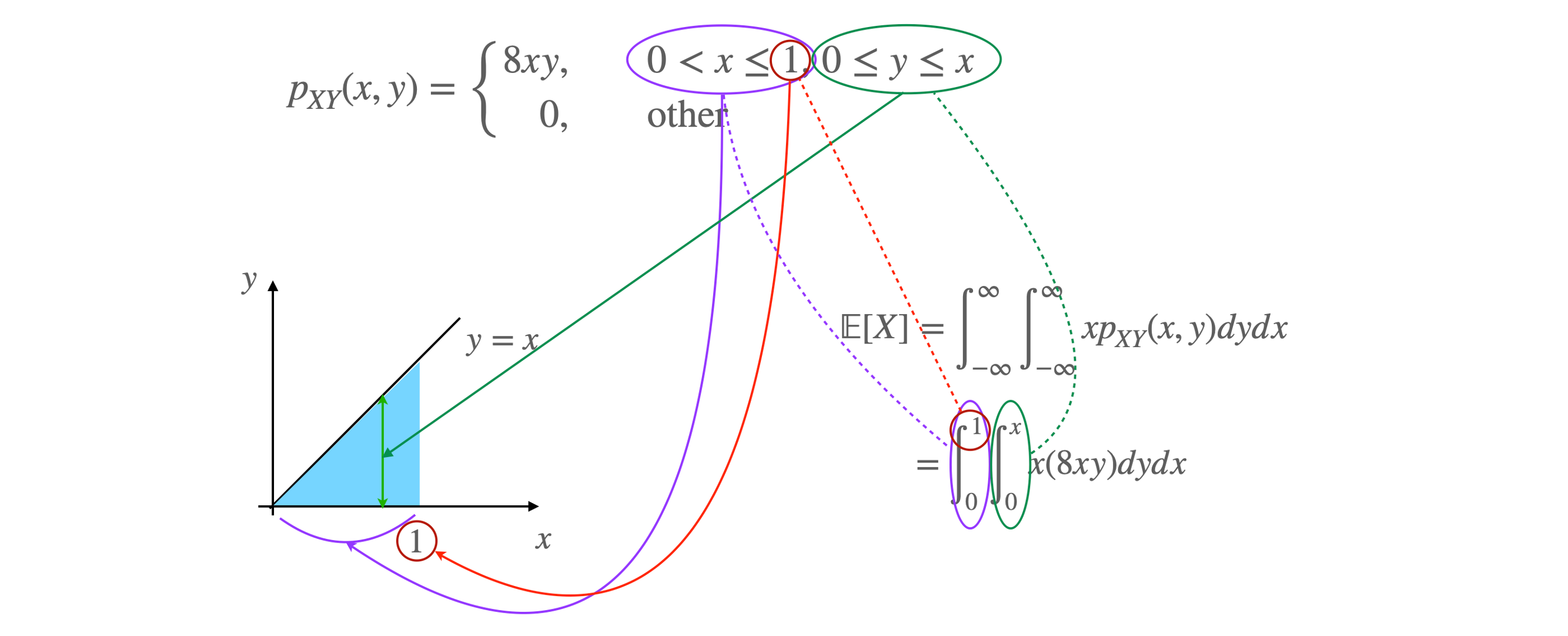
Random Variable X,Y 의 joint probability density function
pXY(x,y)=⎩⎪⎪⎨⎪⎪⎧8xy,0,0<x≤1,0≤y≤xother
일 때,
-
Area of joint probability density function.
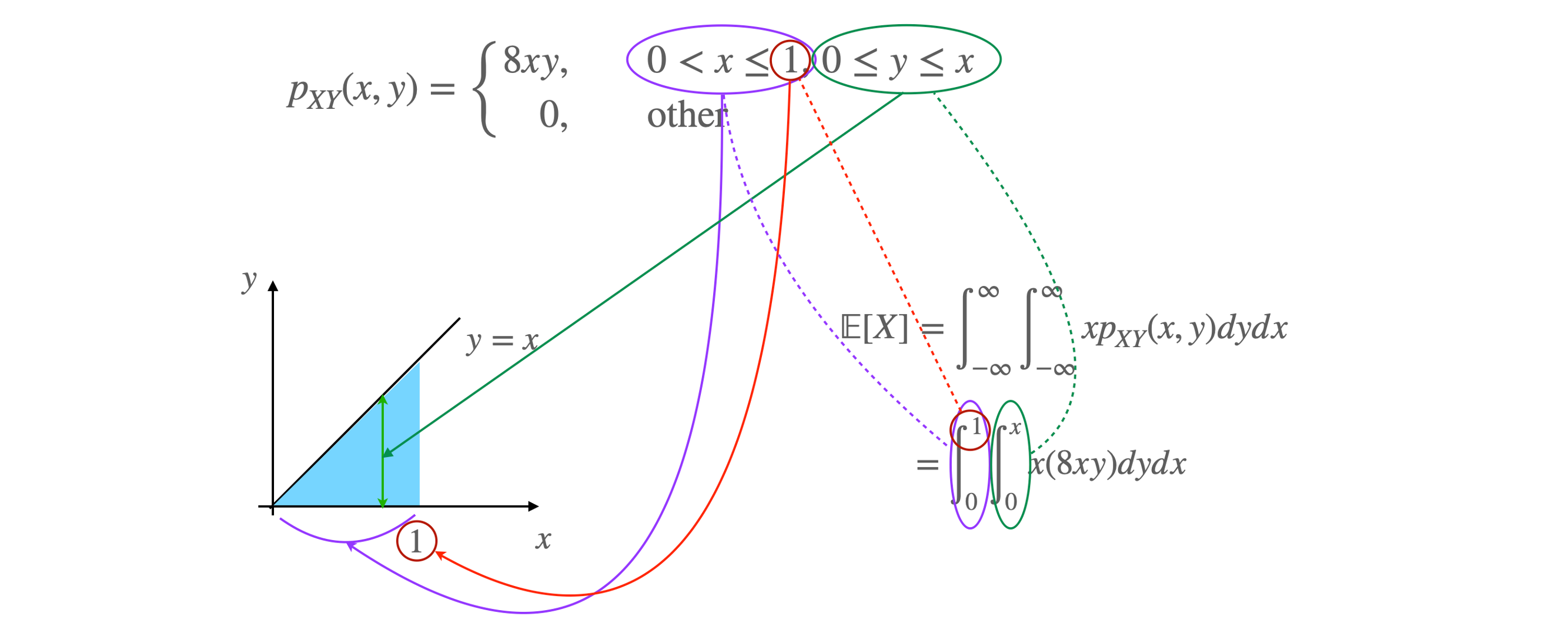
1. Expectation of X
E[X]=∫∞∞xpX(x)dx
를 적용하면
E[X]=∫−∞∞∫−∞∞xpXY(x,y)dydx=∫01∫0xx(8xy)dydx=∫01[4x2y2]0xdx=∫014x4dx=54
2. Expectation of Y
E[Y]=∫∞∞∫∞∞ypXY(x,y)dydx=∫01∫0xy(8xy)dydx=∫01[38xy3]0xdx=∫0138x4dx=158
3. Expectation of X^2
E[X2]=∫−∞∞∫−∞∞x2pXY(x,y)dydx=∫−∞∞∫−∞∞x2(8xy)dydx=∫01[4x3y2]0xdx=∫014x5dx=32
4. Variance of X
Var(X)=E[(X−E[X])2]=∫−∞∞(x−E[X])2pX(x)dx=∫−∞∞(x2−2xE[X]+E[X]2)pX(x)dx=∫−∞∞x2pX(x)dx−∫∞∞2xE[X]pX(x)dx+∫−∞∞E[X]2pX(x)dx=E[X2]−2E[X]E[X]+E[X]2⋅1=E[X2]−(E[X])2=32−(54)2=752
5. Correlation of X, Y
Cor(X,Y)=E[XY]=∫−∞∞∫−∞∞xypXY(x,y)dydx=∫01∫0xxy(8xy)dydx=∫01[38x2y3]0xdx=∫0138x5dx=94
6. Covariance of X, Y
X 의 standard deviation σX=Var(X)
Cov(X,Y)=E[(X−E[X])(Y−E[Y])]=∫−∞∞∫−∞∞(x−E[X])(y−E[Y])pXY(x,y)dydx=∫−∞∞∫−∞∞(xy−E[X]y−xE[Y]+E[X]E[Y])pXY(x,y)dydx=∫−∞∞∫−∞∞xypXY(x,y)dydx−E[X]∫−∞∞ypY(y)dy−E[Y]∫−∞∞xpX(x)dx+E[X]E[Y]=E[XY]−E[X]E[Y]=94−54(158)=2254
7. Conditional Expectation
-
Y of conditional probability density function
pX(x)=∫0x8xydy=8x∫0xydy=8x[21y2]0x=4x3
pY∣X(y∣x)=pX(x)pXY(x,y)=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧x22y,0,0≤y≤x,other0<x≤1
-
X 의 conditional expectation when given Y=y,
E[X∣Y=y]=∫∞∞xpx∣y(x∣y)dx
-
Random Variable X=x 인 Y 의 conditional expectation.
E[Y∣X=x]=∫−∞∞ypY∣X(y∣x)dy=∫0xyx22ydy=[32x3]0x=32x,0<x≤1
-
E[Y∣X=x] 는 실수 x 의 함수로서, 실수 함수
-
Reference (Continuous random variable)
https://online.stat.psu.edu/stat414/lesson/20/20.2