Singular Value Decomposition

d4r6j·2023년 12월 4일

math

목록 보기

2/3

(det)erminant

determinant 가 0 이면, inverse matrix 가 존재하지 않는다.
0 에 가까워지면, 그 행렬이 inverse matrix 가 존재하지 않을 가능성이 크다.

det 의 특성

normalization
- $I(n \times n)$ 는 identity matrix.
- $n \times n$ 의 identity matrix 의 determinant 는 $1$ , ${\rm det}(I) = 1$
row operations
- replacement : $R1 \leftarrow R1 + nR2$ : $\rm det$ 가 변하지 않는다.
- interchange : $R1 \leftrightarrow R2$ : $\rm det$ 의 부호 (sign) 가 바뀐다.
- scaling : $R2 \leftarrow S \cdot R2$ : scaling 을 하게 되면 그 만큼 $\rm det$ 가 곱해진다.
이와 같은 성질은
임의의 주어진 행렬을 Gaussian Elimination 으로 Identity matrix 로 만든 다음, 위 성질에 대입해서 Original Matrix $A$ 의 $\rm det$ 를 계산, 구하는데 사용한다.
예시 1
$\left \vert \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 7 \end{array} \right \vert$

\Rightarrow \left \vert \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 7 \end{array} \right \vert \; \xrightarrow{R2 \leftarrow \frac{1}{2}R2} \; 2\left \vert \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 7 \end{array} \right \vert \; \xrightarrow{R3 \leftarrow \frac{1}{7}R3} \; 7 \cdot 2\left \vert \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right \vert = 14

예시 2
$\left \vert \begin{array}{ccc} 1 & 2 & 3 \\ 0 & 2 & 4 \\ 0 & 0 & 7 \end{array} \right \vert$
$\Rightarrow \left \vert \begin{array}{ccc} 1 & 2 & 3 \\ 0 & 2 & 4 \\ 0 & 0 & 7 \end{array} \right \vert \xrightarrow{R2 \leftarrow \frac{1}{2}R2} 2\left \vert \begin{array}{ccc} 1 & 2 & 3 \\ 0 & 1 & 2 \\ 0 & 0 & 7 \end{array} \right \vert \xrightarrow{R3 \leftarrow \frac{1}{7}R3} 7 \cdot 2\left \vert \begin{array}{ccc} 1 & 2 & 3 \\ 0 & 1 & 2 \\ 0 & 0 & 1 \end{array} \right \vert \\ \quad \\ \xrightarrow{R2 \leftarrow R2 - 2R3}14 \left \vert \begin{array}{ccc} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right \vert \longrightarrow 14\left \vert \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{array} \right \vert = 14$
off-diagonal term 을 없애는 연산들은 모두 replacement. 따라서 $\rm det$ 가 변하지 않는다.

det 의 물리적인 의미

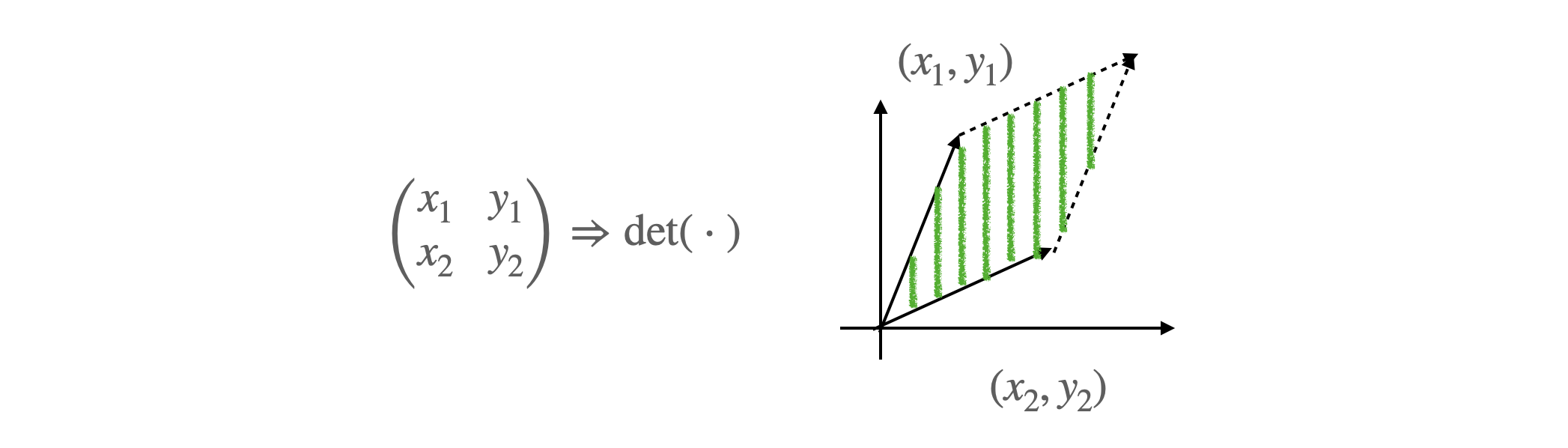
matrix 의 column 들이 이루어지는 공간의 면적을 의미.
$2 \times 2$ matrix 의 $\rm det$ 는 2D 공간 속에서 $(x_1, x_2), (y_1, y_2)$ 두 점으로 이루어진 평행 사변형의 면적. 3D, 4D 로 보게되면 generalize version
matrix 가 만들어 낼 수 있는 공간의 크기와도 이어져 물리적인 의미가 된다.
사용 예시로는
- Normalizing flow 에서 change of variable 이 존재하는데,
- 일반적인 $\rm det$ 를 계산하는 것도, $n \times n$ 도 오래 걸리는데,
이럴 때 upper triangle matrix 의 $\rm det$ 는 diagonal matrix 의 product 성질이고, linear 하게 풀 수 있다. computation efficiency.
Normalizing flow 는 추후에 다시 다룰 예정.

잘 사용하지 않았던 성질들이 최근 deep learning 에서 많이 사용.

determinant $({\rm det})$ property
- ${\rm det}(A) = \vec0 \Longleftrightarrow \; A$ 는 역행렬이 존재 하지 않는다.
- ${\rm det}(AB) = {\rm det}(A) \cdot {\rm det}(B)$
- ${\rm det}(A^{-1}) = \frac{1}{{\rm det}(A)}$
- ${\rm det}(A^{\top}) = {\rm det}(A)$

determinant (det) 란

행렬이 가질 수 있는 basis vector 들이 만들어내는 공간의 부피이다.
matrix 의 column 들을 하나의 vector 로 본다면,
- column 이 2개면 평행 사변형의 공간 면적
- column 이 3개면 공간의 부피
어떤 두 개의 공간 $A, B$ 가 있는데,

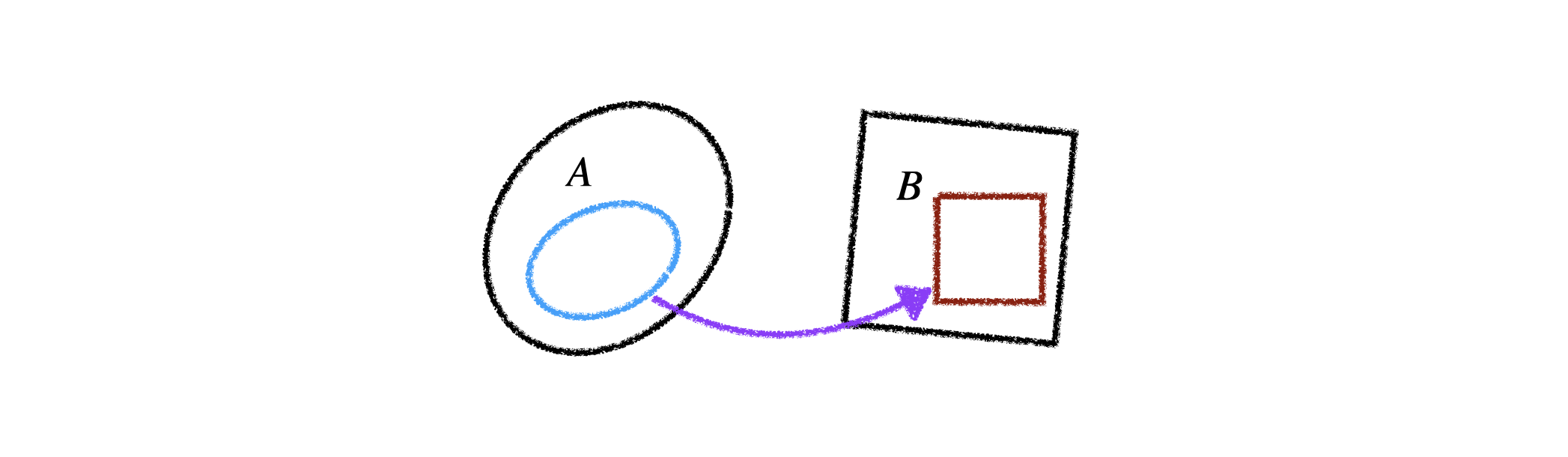
$A$ 에서 $B$ 로 넘어갈 때, $A$ 의 (점, 선, 면적) 이 $B$ 로 갔을 때, Linear map 이면 해당되는 matrix 가 determinant 만큼 늘어나게 된다. 이런 것이 면적, 부피에 해당한다.

eigenvalue, eigenvector

matrix 에 대해 생각을 할 때, 쉽게 이해하기 위해서 square matrix $A \in \mathbb{R}^{n \times n}$ 이라고 가정하자.

definition

An eigenvector of $A$ is a non-zero $\vec x \; s.t. \; A\vec{x} = \lambda\vec{x}$ for some scalar $\lambda$ .
이 성질을 만족하는 것의 $\vec{x}$ 가 eigenvector 이고, 이 때의 $\lambda$ 는 eigenvalue 이다.

$A\vec{x} = \lambda\vec{x}$ 라는 것을 어떻게 풀까?
- 여기서 eigenvector $\vec{x} \neq \vec{0}$
  $\Leftrightarrow A\vec{x} - \lambda\vec{x} = \vec{0} \newline \Leftrightarrow (A - \lambda I)\vec{x} = \vec{0} \newline$
- $A - \lambda I$ 가 invertable 하다면, $(A - \lambda I)^{-1}(A - \lambda I){\vec{x}} = (A - \lambda I)^{-1}\vec{0}$ 이 되고, $\vec{x} = \vec{0}$ 이 된다. 그러나 $\vec{x}$ 는 eigenvector 이고 non-zero 여야 하므로,
- $A - \lambda I$ 가 invertable 하지 않고, 따라서 $\rm det$ 는 $\vec{0}$ 가 되어야 한다
  $\Leftrightarrow {\rm det}(A-\lambda I) = \vec{0}$
- ${\rm det}(A-\lambda I)$ : $A$ 의 characteristic polynomial 이다.

example 1

eigenvalue 를 먼저 찾고, 각 eigenvalue 에 해당하는 eigenvector 를 찾는다.
eigenvalue 는 unique 하게 계산되지만, eigenvector 는 이것을 만족하는 모든 $\vec{x}$ 가 eigenvector 가 된다.
Example : $A = \left[ \begin{array}{cc} 3 & 1 \\ 1 & 3 \end{array} \right]$ 의 eigenvector 들을 찾는다.

$\Rightarrow | A-\lambda I| = \left| \begin{array}{cc} 3-\lambda & 1 \\ 1 & 3 - \lambda \end{array} \right| = (AD-BC) = (3 - \lambda)^2 - 1 = \vec{0}$

$\Rightarrow \lambda^2 - 6\lambda + 8 = (\lambda - 2)(\lambda - 4) = 0 \quad \therefore {\rm \lambda_1} = 2, \quad {\rm \lambda_2} = 4$
- $\lambda_1 = 2$ 에 해당하는 eigenvector 를 찾는다.
  
  $(A - 2I)\vec{x_1} = \vec{0} \Rightarrow \left[ \begin{array}{cc} 1 & 1 \\ 1 & 1 \end{array} \right]\vec{x_1} = \vec{0}$ 따라서 $\left[ \begin{array}{cc} 1 & 1 \\ 1 & 1 \end{array} \right]$ 에 대한 null space 에 해당하는 어떤 $\vec{x_1}$ 을 잡아도 이것은 eigenvalue $\lambda=2$ 에 대응되는 eigenvector 가 된다.
- $\left[ \begin{array}{cc} 1 & 1 \\ 1 & 1 \end{array} \right]\vec{x_1} = \vec{0}$ 에 만족하는 모든 $\vec{x_1}$ , $\left[ \begin{array}{c} 1 \\ -1 \end{array} \right]$ , $\left[ \begin{array}{c} 2 \\ -2 \end{array} \right], \cdots, \left[ \begin{array}{c} n \\ -n \end{array} \right]$ 모두 eigenvector 가 된다.
- eigenvalue 가 $2$ 에 해당하는 eigenvector 는 $\vec{x_1} = \left[ \begin{array}{cc} 1 \\ -1 \end{array} \right]$ 혹은 이것으로 span 되는 모든 vector 들이다.
- 마찬가지로 $\lambda_2 = 4$ 역시 $\left[ \begin{array}{c} 1 \\ 1 \end{array} \right], \cdots, \left[ \begin{array}{c} n \\ n \end{array} \right]$ 로 span 되는 ${\rm span} \left \{ \left[ \begin{array}{cc} 1 \\ 1 \end{array} \right] \right \}$ 의 모든 vector 들이다.
- 이러한 span 되는 공간을 eigenspace 라고 부르기도 한다.
- $A - \lambda I$ 가 있을 때, 이것의 null space 가 모두 eigenvectors 가 된다.
- 이때의 $\lambda$ 는 characteristic polynomial 를 통해서 구해진 $\lambda$ .

example 2

$\left[ \begin{array}{cc} a & b \\ c & d \end{array} \right]$ 의 ${\rm det}$ 를 찾는다.

$\Rightarrow \left| \begin{array}{cc} a & b \\ c & d \end{array} \right| \xrightarrow{R2 \leftarrow R2 - \frac{c}{a} \cdot R1} \left| \begin{array}{cc} a & b \\ 0 & d - \frac{c}{a}b \end{array} \right| = a(d - \frac{c}{a}b) = ad - bc$

이러한 operation 은 값을 변화 시키지 않는다.
- ${\rm det}$ 를 구할 때, upper triangular matrix 까지 구하면, ${\rm det}$ 는 diagonal elements 의 곱 이므로 $a, b, c, d$ 인 $2 \times 2$ 차원 행렬이 있을 때, $ad - bc$ 가 된다.

triangluar matrix 의 determiname 는 diagonal matrics 의 곱 이다.

example 3

$3 \times 3$ matrix $A = \left[ \begin{array}{ccc} 3 & 2 & 3 \\ 0 & 6 & 10 \\ 0 & 0 & 2 \end{array} \right]$ 에 대해서 Eigenvector 를 찾는다.

full matrix 는 계산이 너무 어렵게 된다. null space, row space, column space 와 같은 개념을 잡는 것이 더 중요하다. triangle matrix 만 보자.
- characteristic polynomial 을 계산해보면 $|A-\lambda I|$ 가 되고,
  
  $\Rightarrow | A-\lambda I| = \left| \begin{array}{cc} 3-\lambda & 2 & 3 \\ 0 & 6-\lambda & 10 \\ 0 & 0 & 2-\lambda \end{array} \right| = (3 - \lambda)(6 - \lambda)(2-\lambda) = 0$
  
  $\Rightarrow \lambda_1 = 3, \; \lambda_2 = 6, \; \lambda_3 = 2$
- ${\rm det}$ 를 계산하는 과정에서 $(2, 3, 10)$ 과 같은 것은 replacement 로 없어진다.
- replacement 는 ${\rm det}$ 값이 변하지 않으므로 무시해도 된다.
- upper triangle-matrix 의 ${\rm det}$ 는 diagonal product 와 같다.
  
  3개의 eigenvalue 가 있고, 이것을 $| A-\lambda I|\vec{\rm x} = \vec{0}$ 에 대입하면
  1. $| A - 3I|\vec{\rm x} = \vec{0}$ 로 놓고 null space 를 찾아보면 $\lambda_1 = 3 \rightarrow \vec{x_1} = \left[ \begin{array}{c} 2 & - \frac{5}{2} & 1 \end{array} \right]^{\top}$
  2. $| A - 6I|\vec{\rm x} = \vec{0}$ 로 놓고 null space 를 찾아보면 $\lambda_2 = 6 \rightarrow \vec{x_2} = \left[ \begin{array}{c} 1 & 0 & 0 \end{array} \right]^{\top}$
  3. $| A - 2I|\vec{\rm x} = \vec{0}$ 로 놓고 null space 를 찾아보면 $\lambda_3 = 2 \rightarrow \vec{x_3} = \left[ \begin{array}{c} 2 & 3 & 0 \end{array} \right]^{\top}$
- 물론 이것만 되는 것이 아니라 span 되는 vector 들 모두 eigenvector 가 된다.

eigenvalue, eigenvector 의미.

(중요한 성질) 행렬 $A$ 가 있을 때,
만약 다른 eigenvalues 에 속하는 $n$ 개 $\vec{x_1}, \cdots, \vec{x_n}$ 의 eigenvetors 이 있다면, 그들은 독립적이다.

어떤 행렬의 eigenvector 들이 다른 eigenvalue 에서 온 것이면, 그 eigenvector 들은 모두 lineary independent 하다.
eigenvalue, eigenvector 가 어떤 의미가 있나?
- 공간이 바뀌어도 방향을 유지하는 vector 가 eigenvector.
공간이 바뀌어도 (공간이 바뀐다는 말을 이해하려면 행렬이 가지는 의미를 이해해야 한다.)
- linear map 은 linearity 를 유지하는 조건.
- $f$ 함수, $f(ax + by) = af(x) + bf(y)$ 가 되는 성질을 만족하는 임의의 함수 $f$ 가 linear.
- $f : {\rm x} \rightarrow {\rm y}$ mapping 이 linear 라고 만족을 하면,
  - 어떤 임의의 mapping 을 예로 들면 미분을 들 수 있다.
  - $f$ 라는 mapping 은 행렬 $A$ 로 표현 될 수 있다는 것이 중요한 theorem.
- 행렬 $A$ 의 중요한 의미는 어떤 공간에서 다른 공간으로 넘어가는 transformation 변환을 의미한다.
- 2차원에서 넘긴 공간이 3차원으로 될 수도 있고, 그 반대도 가능한데 차원 축소라고 한다.
- mapping 을 $T$ 라고 하고, 이것에 대응되는 matrix 가 $A_T$ 라고 말할 수 있는 것.
크기에 변화하는 value, 방향을 유지하는 vector
- $A, B$ 공간이 (편의상 두 차원이 같은 차원) 일 때, $A$ 공간에서 $B$ 공간으로 넘어갈 때,
  - vector 의 방향이 달라질 수 있지만, 특정 vector 는 같은 방향으로 유지가 되고 크기만 변한다.
  - 크기의 변화가 eigenvalue 이고, 그 방향이 eigenvector 이다.
- matrix 의 어떤 mapping 이라고 생각하면, eigenvalue 들만 가지고 그 matrix 의 설명이 가능하다.
- 차원 축소를 생각해보자.
  - eigenvector 들은 scale 에 상관 없다.
  - eigenvalue 는 $A$ 공간에서 $B$ 공간으로 넘어갈 때, 해당 축이 $B$ 공간에서 얼마나 의미 있는지 나타낸다.
- $A$ 공간의 차원에서 $B$ 공간의 차원으로 넘어가는 mapping
  - eigenvalue 가 큰 것에 해당하는 eigenvector 들은 $B$ 공간에서의 의미가 커진다.
  - eigenvalue 가 0 이면 $B$ 공간으로 transfer 되면 없어진다.
  - 이 크기에 방향을 유지하는 eigenvector 를 보면, 이 공간의 확장과 축소를 알 수 있다.
- $A \in \mathbb{R}^{n\times n}$ 일 때,
  - $A$ vector 의 eigenvalue $> 1$ 이면, vector 의 방향에 $A$ 를 계속 곱하게 되므로 $A^n\vec{x}$ 는 divergence 한다.
  - $A$ vector 의 eigenvalue $< 1$ 이면, $A^n\vec{x}$ 는 계속 공간을 줄여서 $0$ 에 convergence 한다.

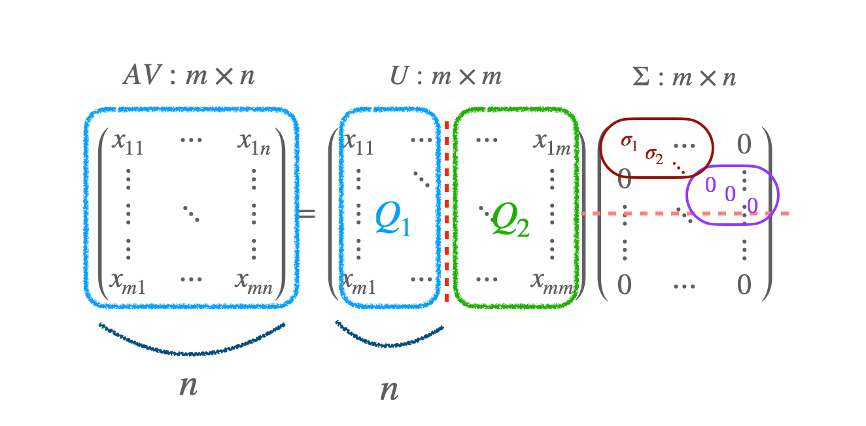
(S)ingular (V)alue (D)ecomposition

SVD 를 이해하는 논리적 흐름은 QR Decompostion 에서 시작.

QR Decomposition

Let $A$ be an $m \times n$ matrix of rank $n$ . Then the QR decomposition $A = QR$ .

rank $n$ 의 $m \times n$ matrix 이 있다고 하자. 일반적으로 $A$ 는 square or tall matrix 이고, fan matrix 는 복잡해진다.
예를 들어 $10 \times 3$ 행렬이 있다고 하면,
- column vector 가 3개 있고, rank 가 $3$ 이면, 모든 column vector 는 linearly independent 하다.

Where $Q \in \mathbb{R}^{m \times n}$ with orthonomal columns, $R$ is upper-triangluer matrix, $n \times n$ , invertable.

이것이 $QR$ decomposition.

tall matrix 의 full rank 가 아니면 $A^{\top}A$ 자체가 invertable 하지 않기 때문에 linearly system 의 solution 이 존재하지 않는다고 해도, 쓸 수는 있지만 solution 을 찾기는 쉽지 않았다.
QR decomposition 에서는 rank 가 $n$ 이라는 조건이 실제로 굉장한 제약 조건이 된다. 따라서 rank 가 $n$ 보다 작으면 (rank difficient) 어떻게 풀 것인가?

QR Decomposition problem

Recall that $A \in \mathbb{R}^{m \times n} \longrightarrow A=QR$ ,
- where $Q$ : orthogonal vector, $R$ : upper-triangular matrix
tall or square matrix 에서 requires ${\rm rank}(A) = n$ 에서 모든 column vector 들이 independent 를 희망.
$m$ 개의 기회를 갖는데, $A$ 라는 행렬을 만들기 위해서 $Q, R$ 이 필요했던 것.
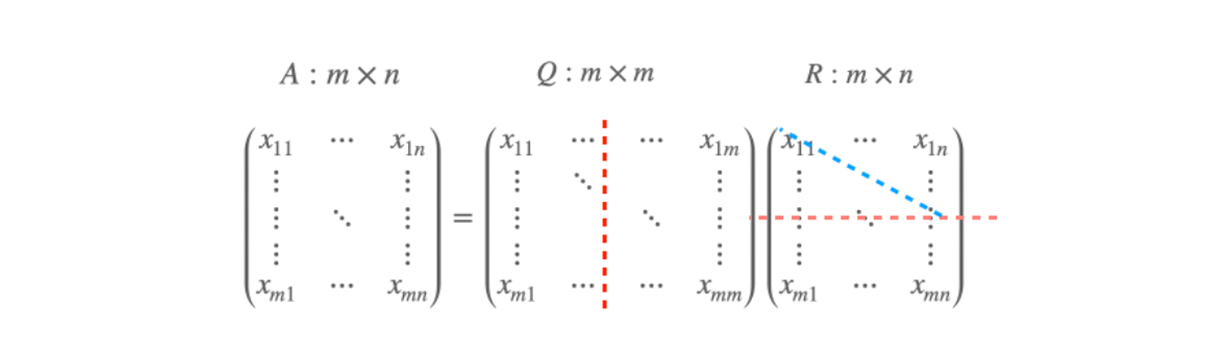
녹색 영역에 해당하는 것은 $R$ 에 대한 basis 가 된다 ?
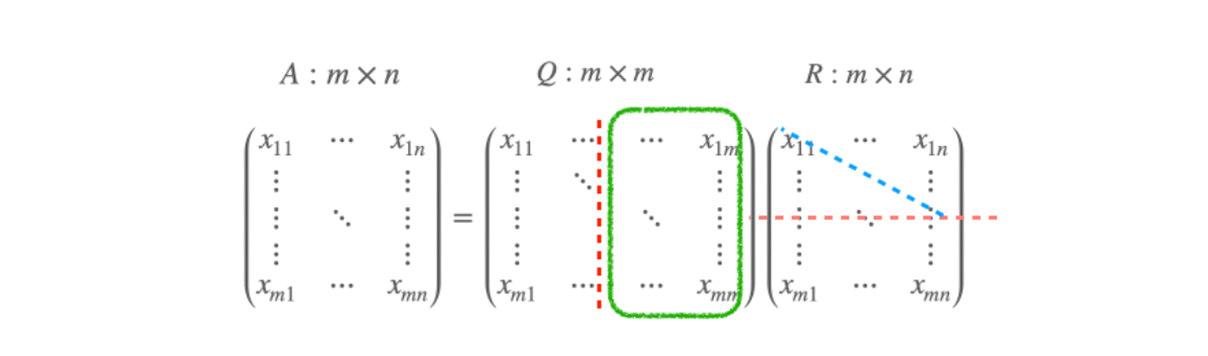
파란 영역 만큼 redundancy 가 있다고 하면, $A$ 에 대한 basis 가 된다.
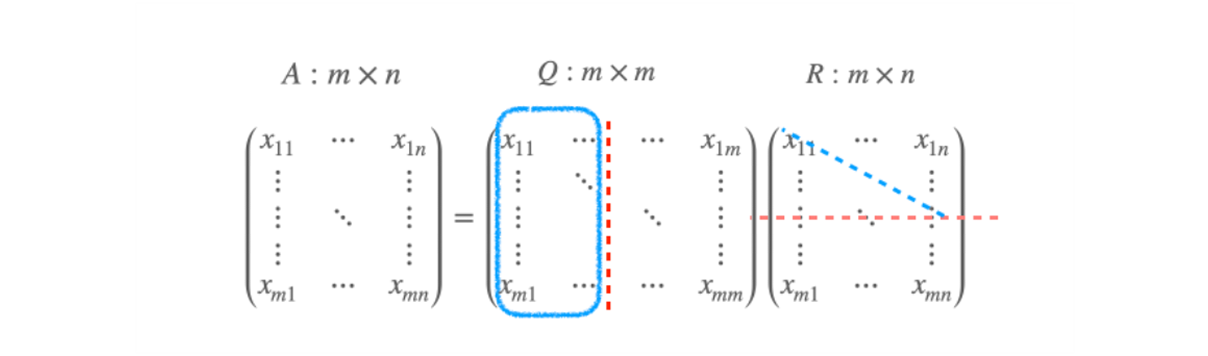
$A$ 의 $m=100$ 이라고 치면, $100$ 차원 전체를 span 할 수 있는 공간 속에 있지만, $n = 50$ 이라고 한다면 $50$ 개 짜리 basis 밖에 못 가지고 있는 $50$ 차원 subspace 가 된다.
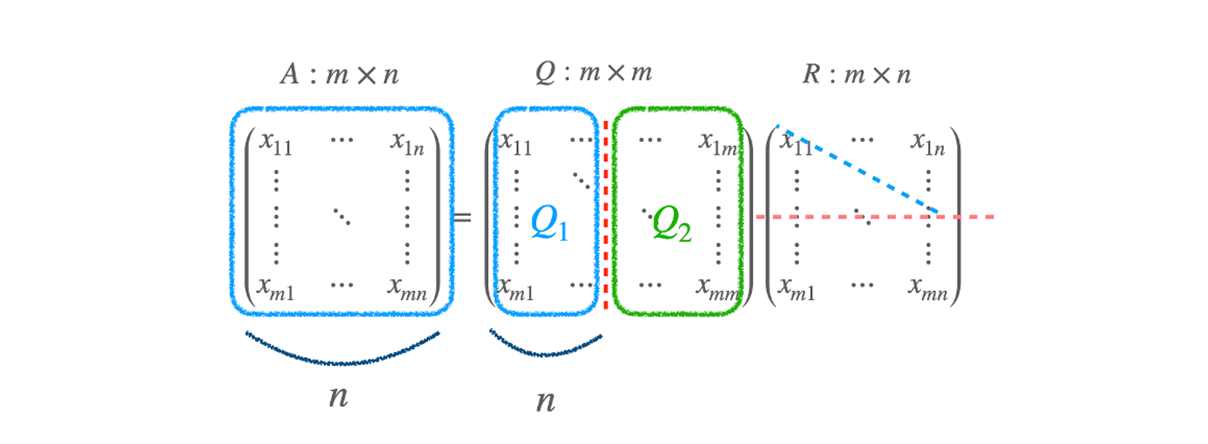
- $Q$ 에서 $Q_1$ 은 원래 $A$ 에 대응되는 basis vector 들, orthonomal 한 $n$ 개의 vector 들이 있다.
- $R$ 에 있는 파란 diagonal term 의 값 들은 모두 $Q_1$ 에 대응되는 값들 이다.
- 나머지 $Q_2$ 는 $A$ column vector 들이 span 하지 못하는 공간들에 대응되는 어떤 vector 로 볼 수 있다.
$A$ vector 가 cover 하는 공간 $Q_1$ 과 cover 하지 못하는 공간 $Q_2$ 로 볼 수 있다.
$A$ vector 가 $rank(A) \neq n$ 일 때, 어떤 일이 발생할지 생각해보면,
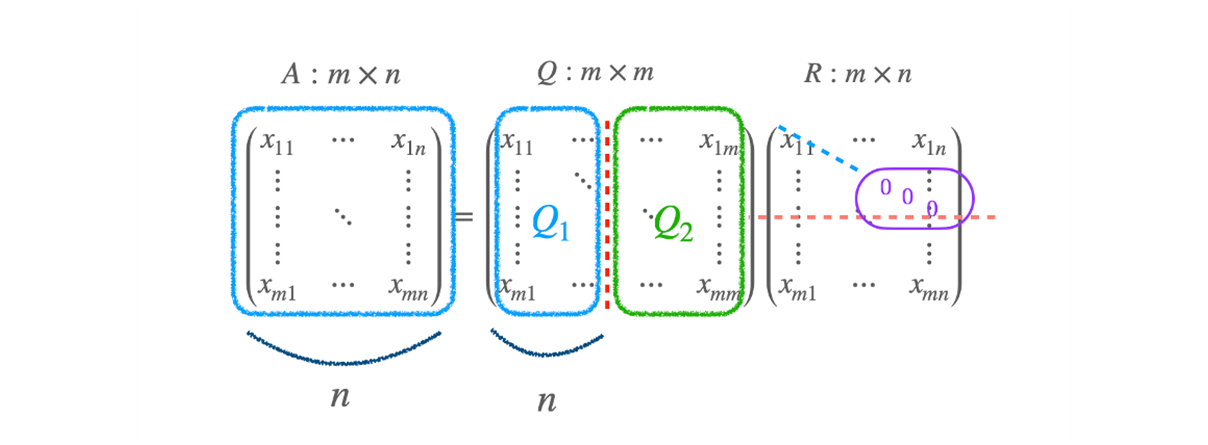
- $R$ 의 diagonal term 의 뒷 부분이 $0$ 으로 채워진다. 따라서 뒷 쪽의 singular value 가 $0$ 이 된다.
- 그렇게 되면, $Q$ 의 basis vector 를 못쓰게 되는데 어떻게 해야하나?

SVD

이와 같이 $A$ 의 colummn vector 들이 모두 independent 가 아니라면?

A = U\Sigma V^{\top}

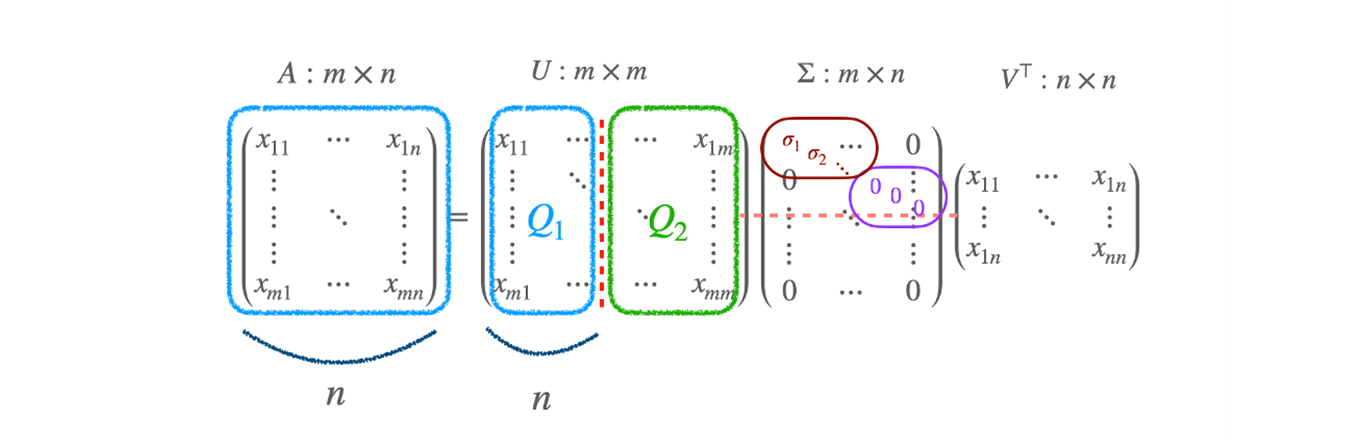
singular values : $\sigma_1, \sigma_2, \cdots$ 가 들어간다.
$\Sigma : m \times n$ 행렬이고, $rank(A)=3$ 이면, 3 까지만 non-zero 값이 들어있다.
4, 5, 6 element 는 $0$ 이 들어가게 된다. 이렇게 $U, \Sigma, V$ 가 된다.
$U, V$ 는 column vector 가 모두 orthonomal vector 인 matrices 이다.
$\Sigma$ 는 square matrix 는 아니지만, diagonal term 만 있는 matrix 이다.
orthonomal vector 는 vector 의 inverse 가 vector 의 transpose 와 같다.

A = U \Sigma V^{\top} = U \Sigma V^{-1} \rightarrow AV = U\Sigma

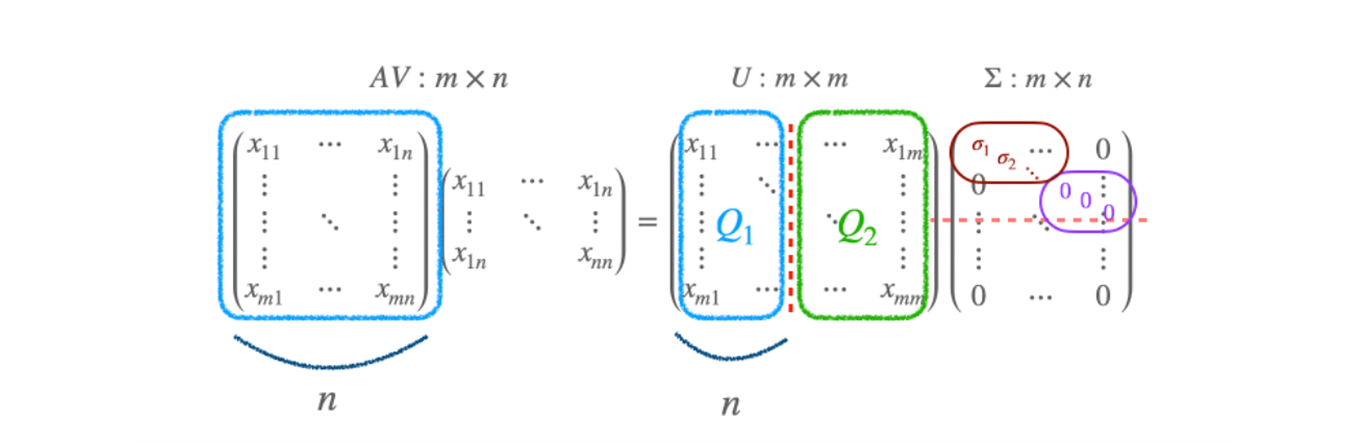
$\Sigma$ matrix (Singular matrix) 는 $A$ 에 대해서 unique 하다. 그러나 $U, V$ 는 unique 하지 않다.
eigenvalue 는 unique 하지만, eigenvector 는 unique 하지 않는 것 처럼..
QR Decomposition 을 이야기 할 때는,
- $A$ 의 rank 가 column 에 대해서 full rank 가 아니면 문제가 있었다.
- 한 쪽이 orthonomal vector 이므로, full rank 가 아니면 $A = QR$ 로 표현할 수 없었기 때문.
SVD 의 수식만 놓고 보면, $AV = U\Sigma$ 는 $QR$ decomposition 과 비슷하다.

Result

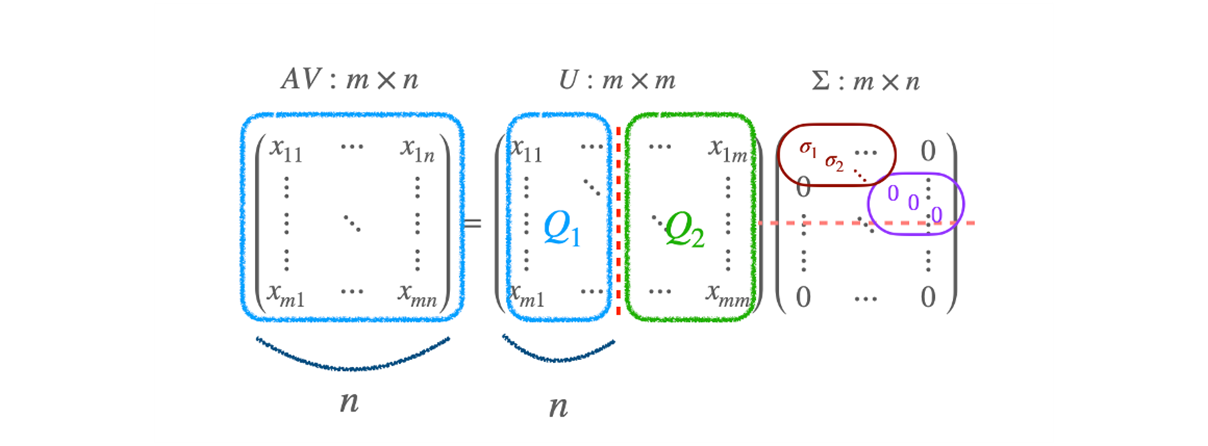
$QRD$ vs $SVD$
- $A$ 와 똑같이 생긴 행렬이 있고,
- $Q$ 행렬인 Orthonomal vector 와 $R$ 행렬인 upper-triangular matrix 로 바꿀수 있다.
- 그런데 $R$ 자리에 $0$ 이 들어가는 것을 허용할 수 없었다.
- $SVD$ 로 $A$ 를 그냥 쓰는 것이 아니라 $V$ 라는 orthonomal matrix 를 곱하면서 가능해졌다.

$U$ or $V^{\top}$
- orthonomal vector 로 되어 있는 square matrix
- 공간을 회전 행렬로 공간 회전 시킨다고 볼 수 있다.
- 회전 행렬이라고 불리는 공간을 $SO(n)$ (Special Orthogonal Group).
- 공간의 양을 그대로 넣은 상태에서 회전을 시키는 것.

$A=QR$ 에서 $R$ 을 쓸 때, diagonal 에서 앞에 singular value 가 차고, 뒷 쪽에 $0$ 이 떨어지게 만들 수 있어야 하는데, 임의의 $A$ matrix 의 정보량이 모든 column 숫자 만큼의 차원을 커버할 수 없다 하더라도 약간 돌아가 있다.

$AV = U\Sigma$ 의 의미.
- $2$ 차원 공간이 있는데, line 은 rank 가 1 이므로, 한 값을 표현할 수 있고, $(x, y)$ 2개로 표현이 가능.
- 이 공간을 적절히 회전 시켜서 1차원으로 만들게 되면 숫자 한 개만으로 표현할 수 있다.
- 이런 회전 역할을 $AV = U\Sigma$ 에서 $V$ 가 해주게 된다.
- 그래서 뒤에 있는 $\Sigma$ 의 diagonal term 의 뒷 부분에 $0$ 이 들어갈 수 있도록 한다.
- $A$ 가 full rank 가 아니면,
  - $V$ 라는 orthogonal vector matrix 를 곱하므로써,
  - $\Sigma$ 라는 diagonal 뒷쪽 에 $0$ 이 들어갈수 있게 회전을 곱해줄 수 있는 성질이 추가.

(SVD) Relation to..

$SVD$ : $A = U\Sigma V^{\top}$ .

여기서는 계산을 편하게 하기 위해서 $A, U, V$ 는 Square matrix 라고 하자.

$SVD$ 의 성질을 이용하기 위해서 $A^{\top}A$ 를 계산해보자.
- $U, V$ 는 orthonomal vector 이기 때문에 $UU^{\top} = I$
- $A^{\top}A = V\Sigma U^{\top}U\Sigma V^{\top} = V(\Sigma^{\top}\Sigma)V^{\top}$

EVD ( Eigenvalue Decomposition )

$A \vec{{\rm x}} = \lambda \vec{{\rm x}}$

Eigenvalue decompostion 을 행렬 form 으로 사용하였다.

$\\ \Longleftrightarrow \;\; A \left[ \begin{array}{c} \vdots & \vdots & & \vdots \\ \vec{x_1} & \vec{x_2} & \cdots & \vec{x_n} \\ \vdots & \vdots & & \vdots \end{array} \right] = \left[ \begin{array}{c} \vdots & \vdots & & \vdots \\ \vec{x_1} & \vec{x_2} & \cdots & \vec{x_n} \\ \vdots & \vdots & & \vdots \end{array} \right] \left[ \begin{array}{c} \lambda_1 & & \\ & \lambda_2 & \\ & & \ddots & \\ & & & \lambda_n \end{array} \right]$
- 이제부터 $\Lambda$ 는 matrix가 된다.
  $\Longrightarrow AX = X\Lambda$

$X$ 는 scale 에 따라 상관 없기 때문에 이것은 orthonomal vector 로 볼 수 있어서 $X \Lambda X^{\top}$ 로 쓸 수 있다.
$SVD$ : $A^{\top}A = V(\Sigma^{\top}\Sigma)V^{\top}$ 수식과 $EVD$ : $A = X\Lambda X^{\top}$ 을 비교해보자.
- $X$ 는 eigen vector 이고, $\Lambda$ eigen value 들이 diagonal term 에 들어가 있는 matrix 이다.
- $\Sigma$ 는 singular value 가 들어가 있는 diagonal matrix 이므로 $\Sigma = \Sigma^{\top}$ 이다.
  
  $\Sigma^{\top}\Sigma = \Sigma^2 = \left[ \begin{array}{c} \sigma_1^2 & & \\ & \sigma_2^2 & \\ & & \ddots & \\ & & & \sigma_n^2 \end{array} \right]$ singular value $\sigma_n^2$ 의 square 가 된다.
- $\Sigma^{\top}\Sigma$ 는 $A^{\top}A$ 에 대한 eigenvalue 로 볼 수 있다.
- singular value 의 제곱 $(\sigma^2_n)$ 은 $A^{\top}A$ 행렬의 eigenvalue 로 볼 수 있다.
- $A$ 의 eigenvalue 가 양수라면, singular 가 같아진다.
- $A$ 의 eigenvalue 가 음수 여도 square root 를 취하므로 똑같은 양수 값이 나온다.

$[\Sigma]_{ii}$ : square root of $i$ th eigenvalue of $A^{\top}A$
- 따라서 singular value (특이값) 는 $A^{\top}A$ 의 eigenvalue 의 square root 이므로 양수여야 한다.

PCA ( Principal Component Analysis )

PCA 는 SVD 와 같다.

$SVD \rightarrow A = U_{m\times m}\Sigma_{m\times n} V^{\top}_{n}$

= \left[ \begin{array}{c} \vdots & \vdots & & \vdots \\ \vec{u_1} & \vec{u_2} & \cdots & \vec{u_m} \\ \vdots & \vdots & & \vdots \\ \vdots & \vdots & & \vdots \end{array} \right] \left[ \begin{array}{c} \sigma_1 & 0 & \cdots & 0 \\ 0 & \sigma_2 & \cdots & \vdots \\ \vdots & 0 & & \sigma_n \\ 0 & \vdots &\cdots & 0 \\ \end{array} \right] \left[ \begin{array}{c} \cdots & v_1 & \cdots \\ \cdots & v_2 & \cdots \\ \vdots & \vdots & \vdots \end{array} \right] = \sum^{n}_{i=1} \sigma_i \vec{u_i}\cdot\vec{v_i}^{\top}

$\vec{u_i}\cdot\vec{v_i}^{\top}$ 은 $m \times n$ matrix 이지만, rank 는 1 이 된다.
vector 2 개만 곱해서 만들었기 때문에, $m \times n$ matrix 이지만 rank 는 1 이다.
- $\sum^{n}_{i=1} \sigma_i \vec{u_i}\cdot\vec{v_i}^{\top}$ 는 $rank$ 1 짜리 $n$ 개가 모여 있는 vector 로 볼 수 있다.
$A$ matrix 를 $n$ 개의 vector 로 보고, $m$ 차원 공간 속에서 살고있는 $n$ 개의 data 라고 본다면
$A= \left[ \begin{array}{c} \vdots & \vdots & & \vdots \\ \vec{a_1} & \vec{a_2} & \cdots & \vec{a_n} \\ \vdots & \vdots & & \vdots \end{array} \right]$
$n$ 개의 vector $\{ \vec{a_1} \cdots, \vec{a_n}\}$ 의 $U_{m\times m}$ vector 들 중의 $r$ 개를 Principle Component 라고 부른다.

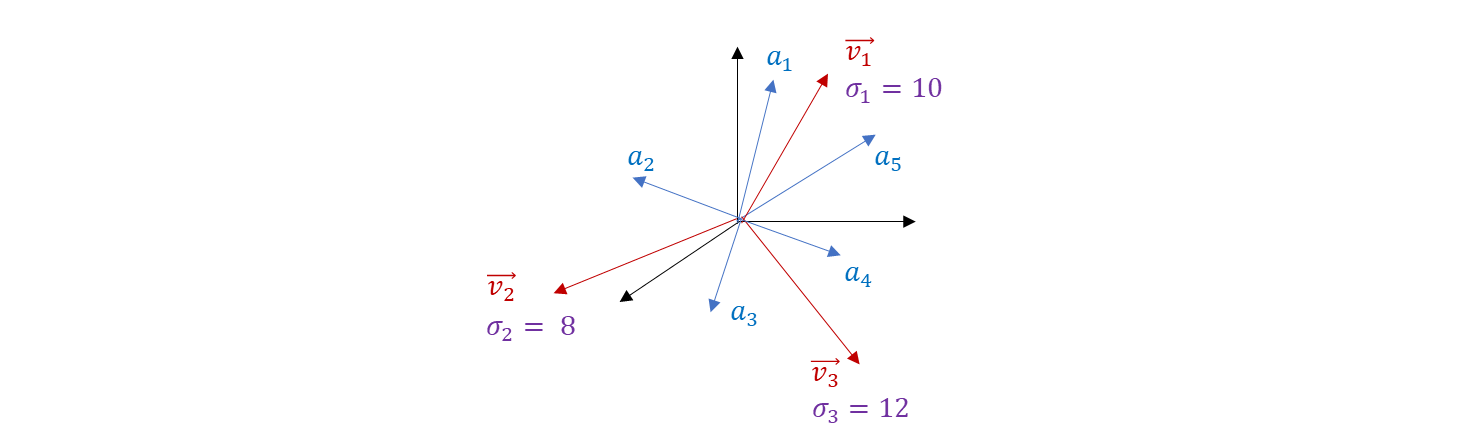
이 3차원 공간 속에는 여러 vector 들이 있다.( $n$ 차원 공간이 가능)
이 데이터들을 잘 설명할 수 있는 vector 는 3개라고 하자. $\vec{v_1}, \vec{v_2}, \vec{v_3}$ 는 orthonomal 하다.
$a_1, a_2, \cdots, a_5$ 의 모든 데이터들을 Principle Component 로 Projection 을 시킨다.
데이터는 $n$ 차원 공간, $r$ 개의 Principle Component 로 projection 을 시키면 vector 를 표현하는 어떤 값이 된다.
$\sigma_1, \sigma_2, \sigma_3$ 은 그 축의 중요도가 들어가 있어서 이 값을 기준으로 sorting 한다.
$\sigma$ 가 큰 몇 개의 vector 에 대응되는 Principle Component 로 주어진 데이터의 설명력을 갖게 된다.
100 차원의 공간에서 Principle Component 를 3개를 잡으면 100 차원에서 3차원으로 reduction 한 것.
$PCA$ 를 하는 과정에 $SVD$ 가 사용됬고, $n$ 차원 공간을 잘 설명하는 축들은 $PCA$ 이고, $SVD$ 의 $U$ 와 같다.