Negative Sampling

d4r6j·2024년 2월 15일

nlp-ai

ml modeling

목록 보기

5/5

Negative Sampling

주어진 문제를 "multi classification" 에서 "binary classificaion" 으로 변환할 수 있지만, 이것으로는 문제가 다 해결되지는 않는다. 이유는 지금까지 긍정적인 예시 (정답) 에 대해서만 학습했기 때문이다. 부정적인 예시 (오답) 를 입력하면 어떤 결과가 나올지 확실하지 않다.

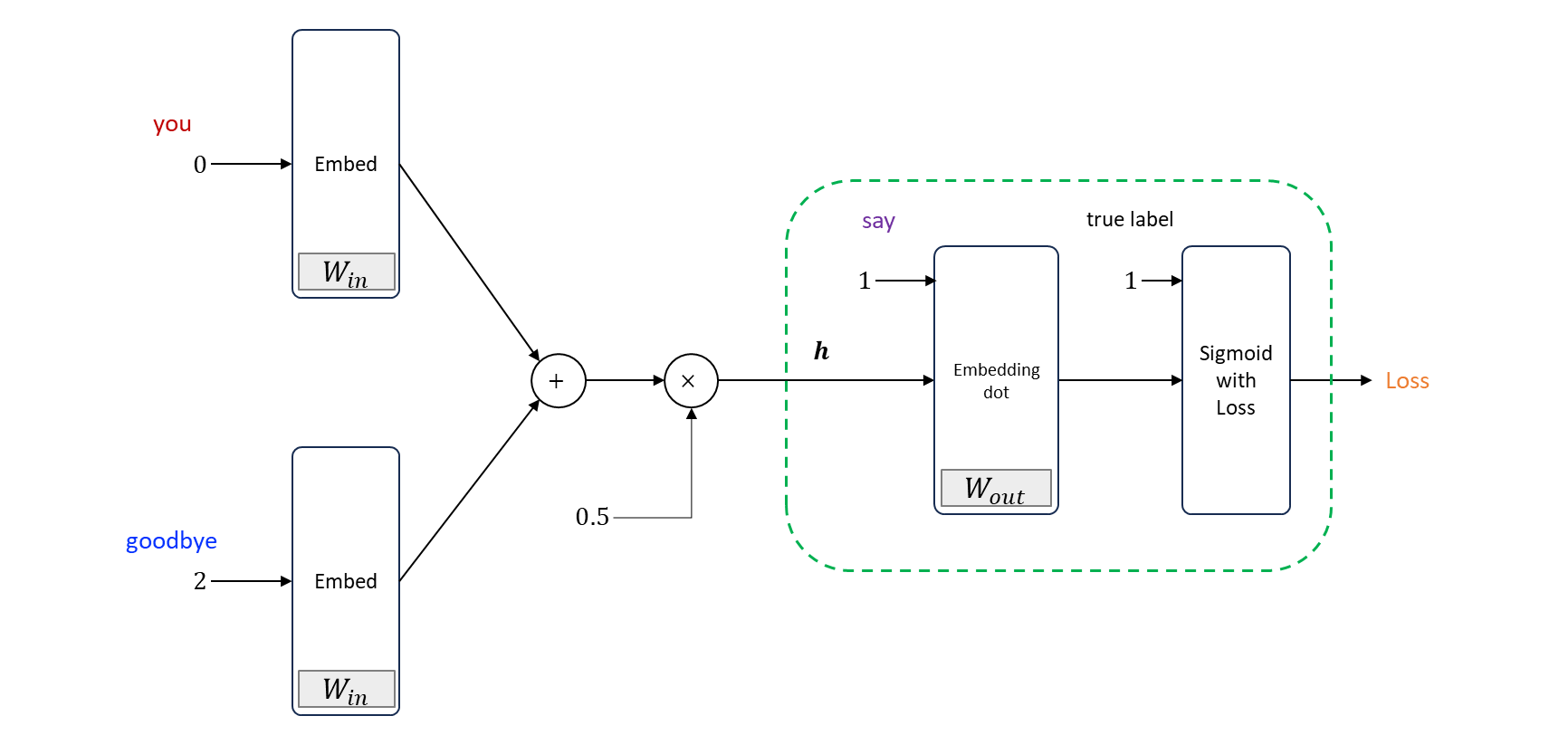
context 가 “you” 와 “goodbye” 이고, 정답 target 이 “say” 인 경우 지금까지 긍정적 예시인 “say” 만을 대상으로 binary classification 을 해왔다.
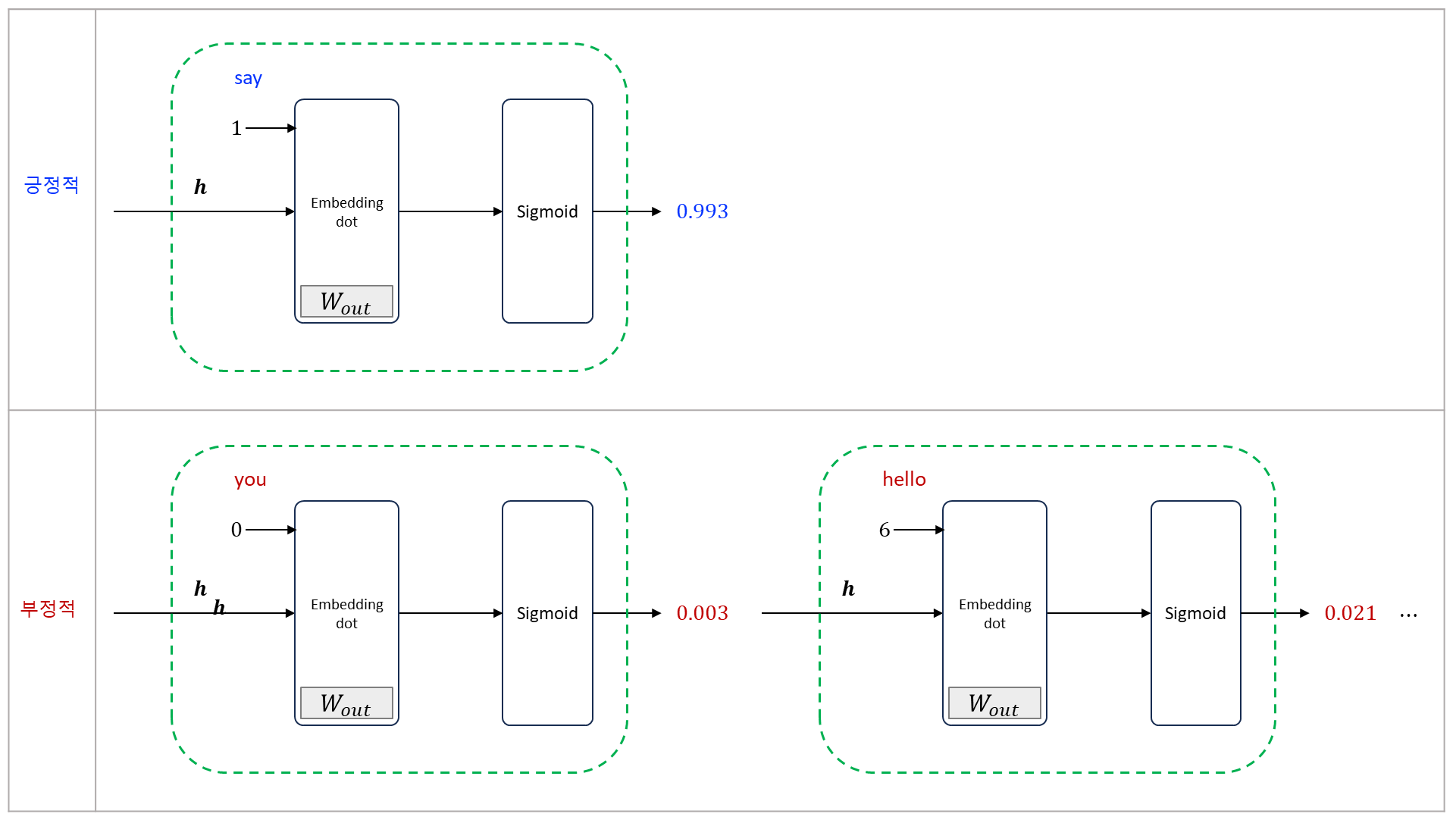
이 모델에서 “좋은 가중치” 가 준비되어 있다면 Sigmoid layer 의 출력 (확률) 은 1에 가까울 것이다. 현재 모델에서는 긍정적 예시 (”say”) 에 대해서는 Sigmoid 계층의 출력을 1에 가깝게 만들었지만, 부정적 예시 (”say” 이외의 단어) 에 대해서는 어떠한 지식도 획득하지 못한다.
원하는 모델은 부정적 예시 (”say” 이외의 단어) 에 대해서는 Sigmoid 계층의 출력을 0에 가깝게 만드는 것이다. 예를 들어 context 가 “you” 와 “goodbye” 일 때, target 이 “hello” 일 확률 (틀릴 단어일 경우의 확률) 은 낮은 값 이어야 바람직하다.
target 이 “hello” 일 확률은 0.021 (2.1%) 이다. 그리고 이런 결과를 만들어주는 가중치가 필요하다.

multi-classification problem 를 binary classification 으로 다루려면 ‘정답 (positive example)’ 과 ‘오답 (negative example)’ 각각에 대해 바르게 (binary) classification 할 수 있어야 한다. 따라서 긍정적 예시와 부정적 예시 모두를 대상으로 문제를 생각해야 한다.
그러나, 모든 부정적 예시를 대상으로 하여 binary classificaion 를 학습 한다면, 어휘수가 늘어나면 감당이 안된다. 그래서 근사적인 해법으로 부정적 예를 몇 개 선택하여 적은 수의 부정적 예를 샘플링하여 사용한다. 이것이 바로 ‘Negative Sampling’ 기법.
Negative sampling 기법은 긍정적 예를 target 으로 한 경우의 손실을 구한다. 그와 동시에 부정적 예를 몇 개 샘플링 하여, 그 부정적 예시에 대해서도 마찬가지로 손실을 구한다. 그리고 각각의 데이터 (긍정적 예와 샘플링된 부정적 예) 의 손실을 더한 값을 최종 손실로 한다.
예를 들어 (긍정적 예의 target “say”) 를 보고 부정적 예의 target 을 2개 (”hello” 와 “I”) 샘플링을 했다고 가정한다. 이제 CBOW 모델의 hidden layer 이후만 주목하면 negative sampling 의 계산 그래프이다.
주의할 부분은 긍정적 예와 부정적 예를 다루는 방식이다. 기존에는 모든 데이터에서 맞는 것만 찾았다면,현재 방식은 틀렸을 때 0 이면 맞게 loss 가 계산되어야 한다.
긍정적 예 (”say”) 에 대해서는 지금 까지 처럼 Sigmoid with Loss layer 에 정답 label 로 “ $1$ ” 을 입력한다. 한편, 부정적 예 (”hello” 와 “I”) 에 대해서는 (부정적 예) 이므로 Sigmoid with Loss layer 에 정답 레이블로 “ $0$ ” 을 입력한다. 그런 다음 각 데이터의 손실을 모두 더해 최종 손실을 출력한다.

Negative Sampling 의 Sampling 기법

부정적 예를 어떻게 샘플링 하느냐 하는 것인데, 다행히 단순히 무작위로 샘플링 하는 것 보다는 corpus 의 통계 데이터를 기초로 샘플링하는 방법이 좋다. corpus 에서 자주 등장하는 단어를 많이 추출하고 드물게 등장하는 단어를 적게 추출하는 방법이다.

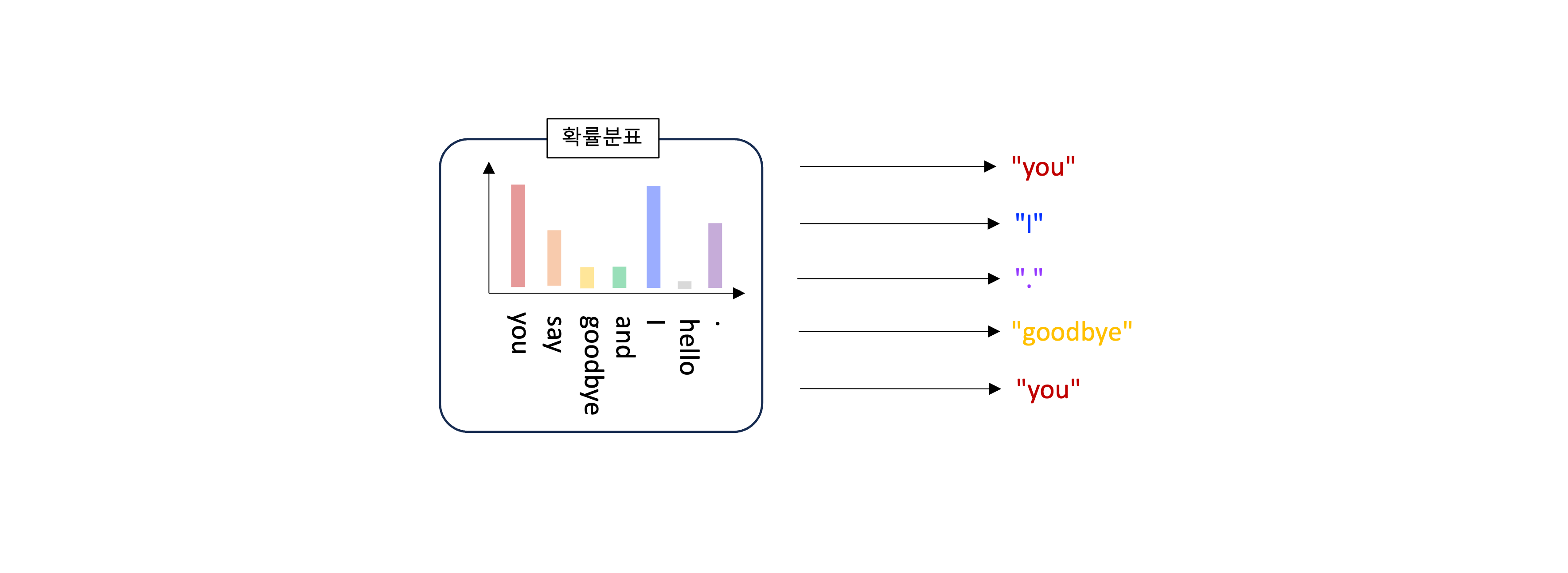
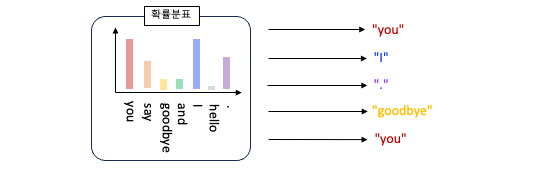
corpus 에서의 단어 빈도를 기준으로 샘플링하려면, 먼저 corpus 에서 각 단어의 출현 횟수를 구해 ‘확률 분포’로 나타낸다. 그런 다음 그 확률 분포 대로 단어를 샘플링하면 된다.
corpus 에서의 단어별 출현 횟수를 바탕으로 확률 분포를 구한 다음, 그 확률 분포에 따라서 sampling 을 수행하기만 하면 된다. 확률 분포 대로 샘플링 하므로 corpus 에서 자주 등장하는 단어는 선택될 가능성이 높다. 확률분포에 따라 샘플링을 여러 번 수행한다. 같은 이유로, ‘희소한 단어’ 는 선택되기 어렵다.
Negative sampling 에서는 부정적 예를 가능한 많이 다루는 것이 좋다. 계산량 문제 때문에 적은 수 (5개나 10개 등) 으로 한정해야 한다. 그런데 우연히도 ‘희소한 단어’ 만 선택 되었다면 어떻게 될까? 당연히 결과도 나빠질 것이다. 왜냐하면 실전 문제에서도 희소한 단어는 거의 출현하지 않기 때문이다. 즉, 드문 단어를 잘 처리하는 일은 중요도가 낮다. 그보다는 흔한 단어를 잘 처리하는 편이 좋은 결과로 이어질 것이다.

확률 분포에 따라 샘플링하는 예를 파이썬 코드로 보자. numpy 의 np.random.choice() 메서드를 사용할 수 있다. 이 메서드의 사용법을 보여주는 예를 몇 가지 살펴보자.

 
>>> import numpy as np

# 0 에서 9까지이ㅡ 숫자 중 하나를 무작위로 sampling
>>> np.random.choice(10)
3
>>> np.random.choice(10)
9

# words 에서 하나만 무작위로 sampling
>>> words = ['you', 'say', 'goodbye', 'I', 'hello', '.']
>>> np.random.choice(words)
'I'

# 5개만 무작위로 샘플링 (중복 있음)
>>> np.random.choice(words, size=5)
array(['say', 'I', '.', 'hello', 'hello'], dtype='<U7')

# 5개만 무작위로 샘플링 (중복 없음)
>>> np.random.choice(words, size=5, replace=False)
array(['I', 'goodbye', 'say', 'hello', '.'], dtype='<U7')

# 확률 분포에 따라 sampling
>>> p = [0.5, 0.1, 0.05, 0.2, 0.05, 0.1]
>>> np.random.choice(words, p=p)
'I'
>>> np.random.choice(words, p=p)
'you'
>>> np.random.choice(words, p=p)
'you'
>>> np.random.choice(words, p=p)
'you'

이 코드에서 보면 np.random.choice() 는 무작위 sampling 용도로 이용할 수 있다. 이 때, 인수로 size 를 지정하면 sampling 을 size 만큼 수행한다.
또한 인수에 replace=False 를 지정하면 sampling 시 중복을 없애준다.
그리고 인수 $p$ 에 확률 분포를 담은 리스트를 지정하면 그 확률 분포 대로 sampling 을 한다.
이 함수를 사용해 부정적 예를 sampling 한다.

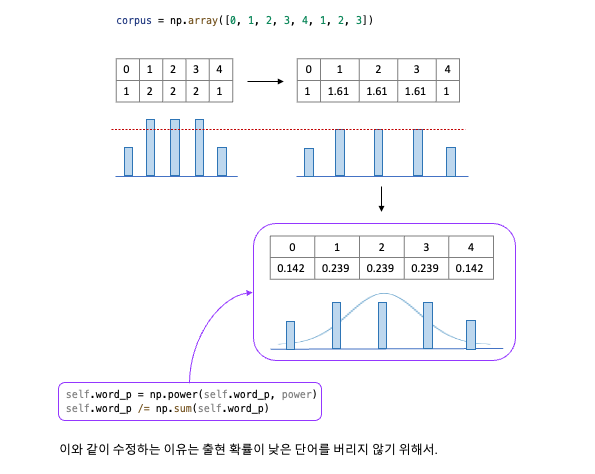
word2vec 의 negative sampling 에서는 앞의 확률 분포에서 한 가지를 수정하라고 권고 하고 있다. 기본 확률 분포에 $0.75$ 를 제곱하는 것.
$P'(w_i) = \frac{P(w_i)^{0.75}}{\sum^{n}_{j}p(w_j)^{0.75}}$
여기서 $P(w_i)$ 는 $i$ 번째 단어의 확률을 뜻한다. 단순히 원래 확률 분포의 각 요소를 $0.75$ 제곱 할 뿐이다. 다만 수정 후에도 확률 총합은 1이 되어야 하므로 분모로는 ‘수정 후 확률 분포의 총합’이 필요하다.
이와 같이 수정하는 이유는 출현 확률이 낮은 단어를 버리지 않기 위함이다. 더 정확하게 말하면 ‘ $0.75$ 를 제곱’ 함으로써, 원래 확률이 낮은 단어의 확률을 살짝 높일 수 있다.
```
>>> p = [0.7, 0.29, 0.01]
>>> new_p = np.power(p, 0.75)
>>> new_p /= np.sum(new_p)
>>> print(new_p)
[0.64196878 0.33150408 0.02652714]
```
이 예에서 보듯 수정 전 확률이 $0.01 (1\%)$ 이던 원소가, 수정 후에는 0.0265 … 약 $(2.65\%)$ 로 높아졌다. 이처럼 낮은 확률 단어가 조금 더 쉽게 샘플링 되도록 하기 위한 구제 조치로써 $0.75$ 제곱을 수행한다. 참고로 $0.75$ 라는 수치에는 이론적인 의미는 없으니 다른 값으로 설정해도 된다.
Negative Sampling STEP
1. corpus 에서 단어의 확률 분포를 만들고
2. $0.75$ 를 곱한 다음
  $P'(w_i) = \frac{P(w_i)^{0.75}}{\sum^{n}_{j}p(w_j)^{0.75}}$
3. np.random.choice() 를 사용해 부정적 예시를 sampling 한다.
```
# 확률 분포에 따라 sampling
>>> p = [0.5, 0.1, 0.05, 0.2, 0.05, 0.1]
>>> np.random.choice(words, p=p)
'I'
```
유니그램 (unigram) 이란 ‘하나의 연속된 단어’ 를 뜻한다. 바이그램 (bigram) 은 ‘2개의 연속된 단어’ 를, 트라이그램 (trigram) 은 ‘3개의 연속된 단어’ 를 뜻한다. 그래서 UnigramSample 클래스의 이름에는 한 단어를 대상으로 확률 분포를 만든다는 의미가 녹아있다. 만약 이를 bigram 버전으로 만든다면
```
('you', 'say'), ('you', 'goodbye') ...
```
같은 두 단어로 구성된 대상에 대한 확률 분포를 만들게 된다.

UnigramSampler class 는 초기화 시 3개의 parameter 를 받는다.

# Unigram Sampler class.
class UnigramSampler:
  def __init__(self, corpus, sample_size, power=0.75):
      self.sample_size = sample_size
      self.vocab_size = None
      self.word_p = None

      counts = collections.Counter()
      for word_id in corpus:
          counts[word_id] += 1
      
      vocab_size = len(counts)
      self.vocab_size = vocab_size
      
      self.word_p = np.zeros(vocab_size)
      for i in range(vocab_size):
          self.word_p[i] = counts[i]

      self.word_p = np.power(self.word_p, power)
      self.word_p /= np.sum(self.word_p)

corpus : 단어 ID 목록
power : 확률 분포에 '제곱' 할 값 (기본 값은 0.75)
sample_size : 부정적 예시 sampling 을 수행하는 횟수

또한 UnigramSampler class 는 get_negative_sample(target) 메서드를 제공한다.
- 이 method 는 target 인수로 지정한 단어를 긍정적 예로 해석하고, 그 외의 단어 ID 를 샘플링한다. (즉, 부정적 예를 골라준다).
- positive example 로 [1, 3, 0] 이라는 3개의 데이터를 mini-batch 로 다뤘다. 이 각각의 데이터에 대해서 부정적 예를 2개씩 sampling 한다.
- 이 예에서는
  - 첫 번째 데이터에 대한 부정적 예시는 [3 4]
  - 두 번째 데이터에 대한 부정적 예시는 [1 2]
  - 세 번째 데이터에 대한 부정적 예시는 [2 3]
이 뽑혔음 을 알 수 있다. ( 실행할 때마다 결과가 달라진다. np.random.choice 때문 ) 부정적인 예시를 샘플링 할 수 있게 되었다.
```
from cbow.negative_sampling_layer import UnigramSampler

corpus = np.array([0, 1, 2, 3, 4, 1, 2, 3])
power = 0.75
sample_size=2

sampler = UnigramSampler(corpus=corpus,
                         power=power,
                         sample_size=sample_size)

target = np.array([1, 3, 0])
negative_sample = sampler.get_negative_sample(target=target)
print(negative_sample)

# [[3 4]
#  [1 2]
#  [3 2]]
```

Code example


# positive example : target=[1, 3, 0]
def get_negative_sample(self, target, use_gpu=False):
    batch_size = target.shape[0] # 3

    if use_gpu is False:
        negative_sample = np.zeros(
            (batch_size, self.sample_size), # self.sample_size : 2
            dtype=np.int32
        )

        for i in range(batch_size):
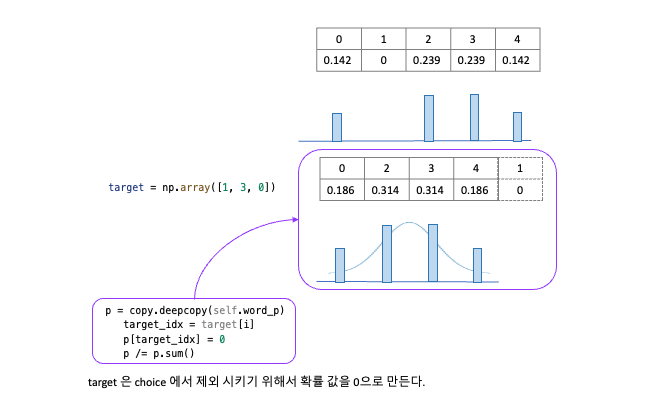
            p = copy.deepcopy(self.word_p)
            target_idx = target[i]
            p[target_idx] = 0
            p /= p.sum()
            negative_sample[i, :] = \
                np.random.choice(
                    self.vocab_size,
                    size=self.sample_size,
                    replace=False,
                    p=p)
    else:
        negative_sample = np.random.choice(
            self.vocab_size,
            size=(batch_size, self.sample_size),
            replace=True,
            p=self.word_p
        )
    
    return negative_sample


negative_sample = np.zeros(
    (batch_size, self.sample_size), # self.sample_size : 2
    dtype=np.int32
)

{\rm negative \; sample} = \left [ \begin{array}{cc} 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{array} \right ]

아예 날리는 것이 아니라 index 는 살려서 np.random.choice 를 할 때, 항목의 갱신은 없게 하되, 확률 값을 $0$ 으로 날려서 probability 에 걸리지 않게 만든다.
```
for i in range(batch_size): # batch_size : 3. (0, 1, 2)
    p = copy.deepcopy(self.word_p)
    target_idx = target[i]
    p[target_idx] = 0
    p /= p.sum()
    negative_sample[i, :] = \ # 0th, 1st, 2nd
        np.random.choice(
            self.vocab_size,
            size=self.sample_size,
            replace=False,
            p=p)
```
$\left [ \begin{array}{cc} 4 & 2 \\ 0 & 0 \\ 0 & 0 \end{array} \right ] \longrightarrow \left [ \begin{array}{cc} 4 & 2 \\ 1 & 2 \\ 0 & 0 \end{array} \right ] \longrightarrow \left [ \begin{array}{cc} 4 & 2 \\ 1 & 2 \\ 1 & 3 \end{array} \right ]$

Ref.

밑바닥부터 시작하는 딥러닝 2nd

d4r6j

이전 포스트

Negative Sampling

ml modeling

Negative Sampling

Negative Sampling 의 Sampling 기법

Code example

Ref.

Plot for Evaluation

0개의 댓글