[ PEFT ] Parameter-Efficient Fine-Tuning

d4r6j·2024년 5월 8일

ml-modeling

methodology-ai

목록 보기

1/8

RoLA

Low-Rank Adaptation of Large Language Models

Understanding

Pretrained LLM 은 다양한 task 에 걸쳐서 다재다능 하기 때문에 foundation 모델 이라고 말하지만, 특정 dataset 이나 tasks 를 위해 Pretrained LLM 을 조정하는 것이 유용한 경우가 많으며, 그것은 finetuning 을 통해 수행 할 수 있다.
finetuning 은 많은 비용이 드는 사전 학습 없이 특정 도메인에서 적응할 수 있지만, 아주 큰 모델의 경우에는 모든 레이어들을 업데이트 하는 것은 여전히 비용이 너무 비싸다.
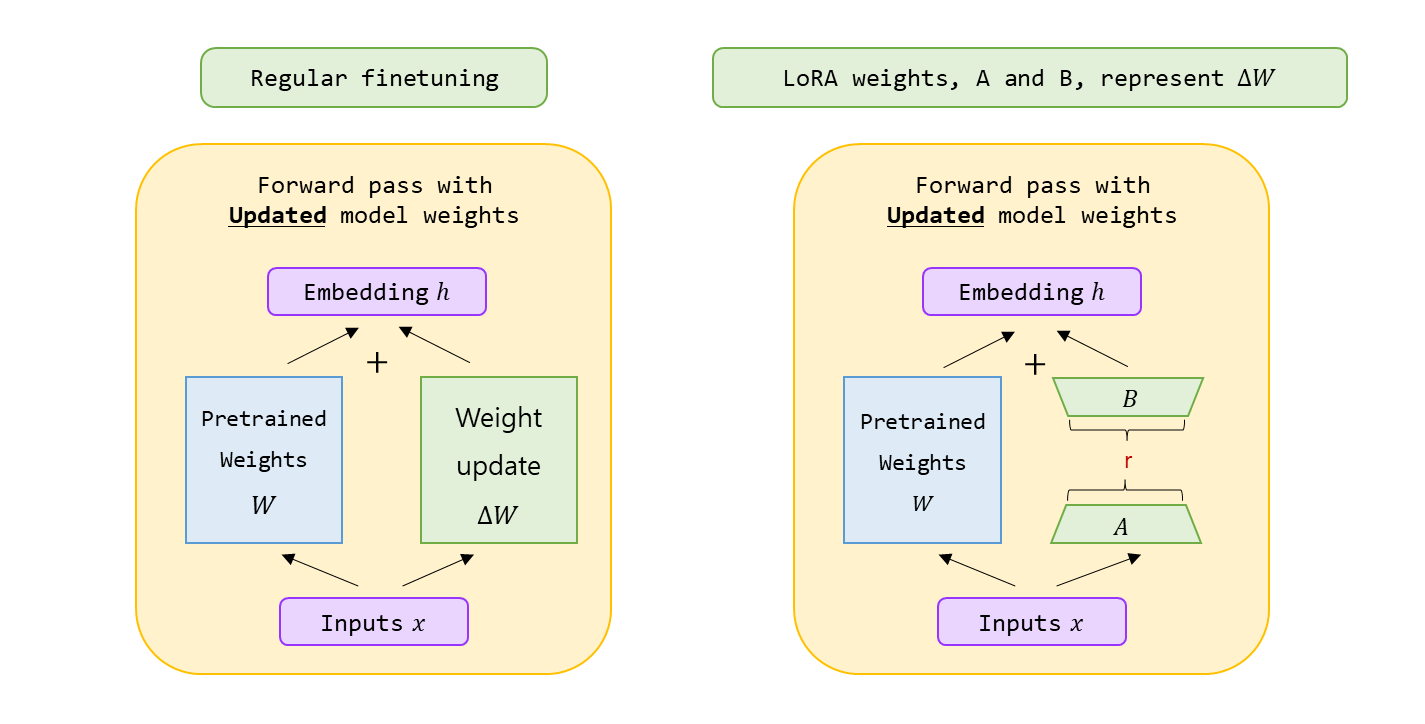
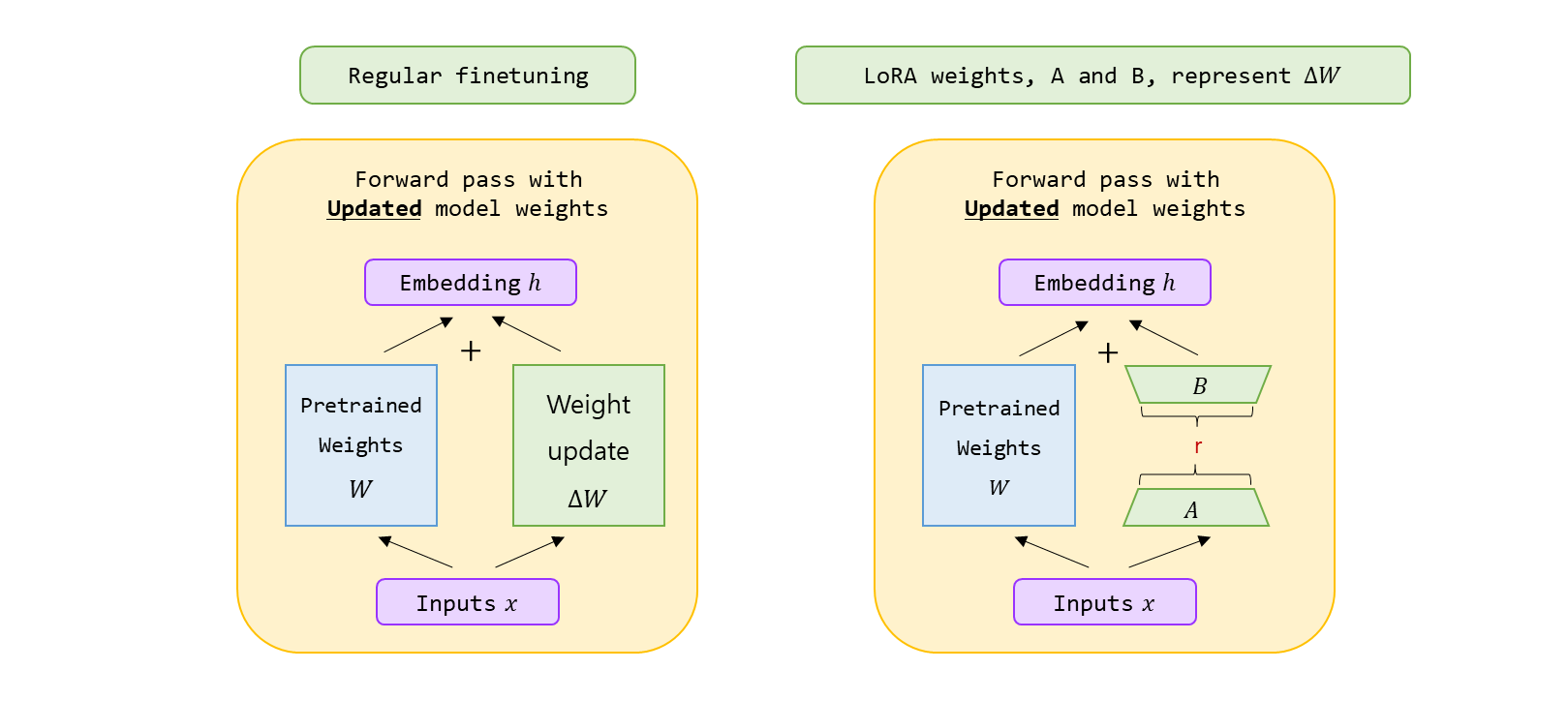
LoRA 는 LLMs 를 더 효율적으로 finetune 하기 위한 유명한 기술이다. DNN 의 모든 parameter 를 조정하는 대신, low-rank matrices 의 작은 집합만 update 하는데 focus 를 둔다. LoRA 는 훈련하는 동안 레이어 가중치 변화 $\Delta W$ 를 low-rank 형태로 근사한다.

several key advantages

pre-trained 모델을 공유할 수 있고, 다른 task 들을 위해 작은 LoRA 모듈 들을 build 하는 데 사용할 수 있다. 공유된 pre-trained 모델 을 freeze 하고 매트릭스 $A$ 와 $B$ 로 대체 함으로써 효율적으로 task 를 switch 하여 storage 요구 사항과 task-switching 에 발생하는 overhead 를 크게 줄일 수 있다.
거의 대부분의 parameter 에서 gradient 들을 계산하거나 최적화 상태를 유지할 필요가 없기 때문에 LoRA 는 adaptive optimizer 를 사용할 때, 훈련은 더욱 효율적으로 만들고, hardware barrier 를 3배 까지 낮춘다.
간단한 linear design 를 배포할 때 훈련 가능한 행렬의 고정된 weights 와 병합 하여, 구조적으로 전체 fine-tuned 모델과 비교하여 inferecne latency 가 발생하지 않는다.
많은 사전 방법들과 orthogonal (직교 한다는 뜻인데 아마 독립적이라고 표현하고 싶은 것 같다.) 하고 prefix-tuning 과 같은 많은 방법들과 조합할 수 있다.

methodology from scratch

개념적인 설명은 때때로 추상적일 수 있으므로, 그것이 얼마나 잘 동작 하는지 더 잘 알기 위해서 LoRA 를 직접 개발해보자.

class LoRALayer(nn.Module):
    def __init__(self, in_dim, out_dim, rank, alpha):
        super().__init__()
        std_dev = 1 / torch.sqrt(torch.tensor(rank).float())
        self.A = nn.Parameter(torch.randn(in_dim, rank) * std_dev)
        self.B = nn.Parameter(torch.zeros(rank, out_dim))
        self.alpha = alpha
    
    def forward(self, x):
        x = self.alpha * (x @ self.A @ self.B)
        return x

in_dim : LoRA 를 사용하여 수정하기를 원하는 layer 의 input 차원.

out_dim : 해당 layer 의 output 차원

행렬 𝐴,𝐵 의 r ( rank ) 는 LoRA 에 의해 도입된, 추가적인 매개변수의 수와 복잡성을 제어하는 하이퍼 파라미터이다. 여기서 또 다른 하이퍼파라미터, scaling factor alpha 를 더한다.

alpha : LoRA layer 에 의한 도입으로 모델의 존재하는 가중치에 대한 변화의 크기를 결정.

self.alpha * ( x @ self.A @ self.B )

\alpha \cdot \left(\mathbf{x} \times A \times B \right)

𝛼 의 값이 높을수록 모델의 behavior 가 더 크게 조정이 되고, 값이 낮을수록 결과에 더 미묘한 변화가 생긴다.

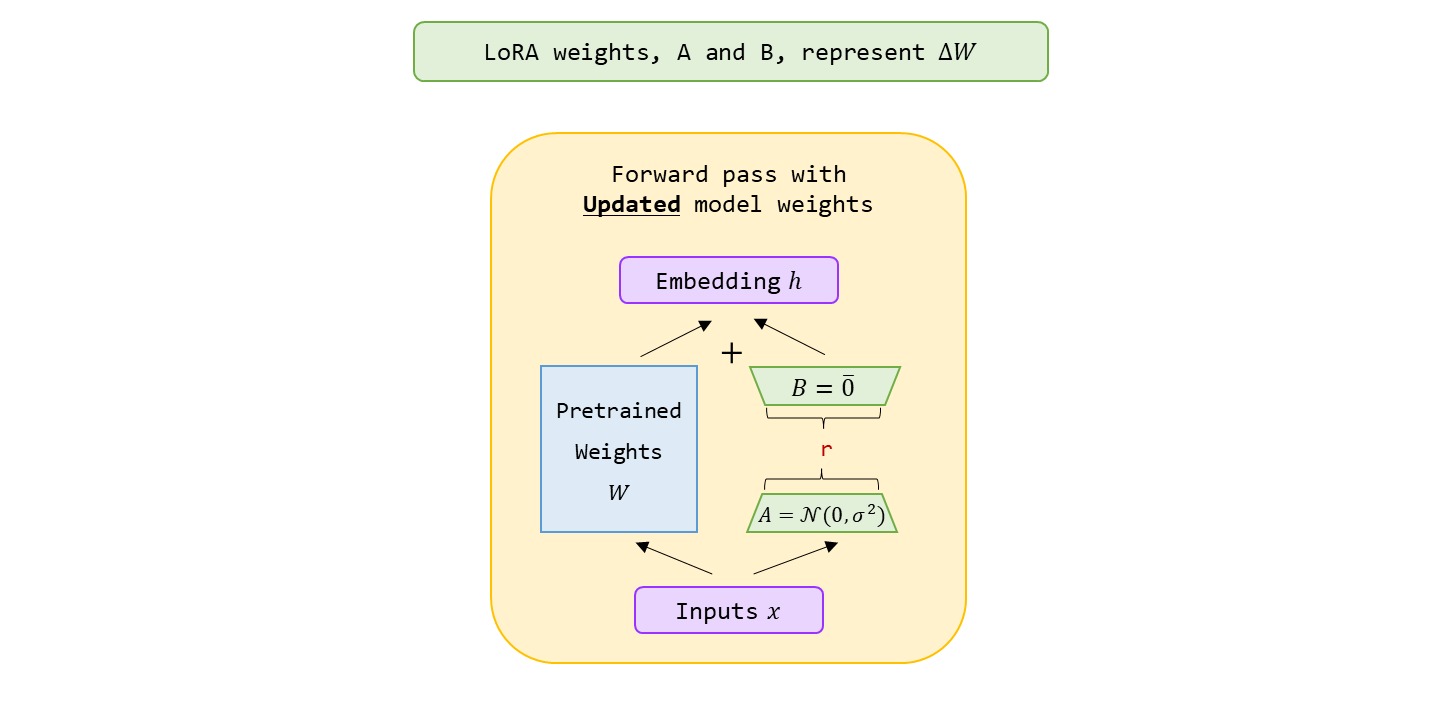
또 하나 주의할 점은, $A$ 를 random 분포로부터 작은 값으로 초기화를 시킨다. 여기서 이 분포의 표준 편차는 $\sqrt{r}$ (sqaure root of the rank) 에 의해 결정된다. (이 선택은 𝐴 가 너무 크지 않게 초기 값을 보장한다.) 그러나 𝐵 는 $\bar{0}$ 이다.
훈련 초기에 $A$ 와 $B$ 가 backpropagtion 을 통해 업데이트 되기 전, $B=0$ 이면 $AB = 0$ 으로 LoRALayer 는 원래의 가중치에 영향을 가하지 않기 위해서 이다.
기존의 PyTorch 모델들을 수정하여 LoRA 를 구현할 때, linear layers 의 LoRA-modification 과 같은 것을 구현하는 쉬운 방법은 기존에 개발한 LoRALayer 와 Linear layer 를 조합한 LinearWithLoRA layer 로 Linear layer 를 대체하는 것이다.

class LinearWithLoRA(nn.Module):
    def __init__(self, linear, rank, alpha):
        super().__init__()
        self.linear = linear
        self.lora = LoRALayer(
            linear.in_features, linear.out_features, rank, alpha
        )
        
    def forward(self, x):
        return self.linear(x) + self.lora(x)

DoRA

Weight-Decomposed Low-Rank Adaptation

Abstract

DoRA 는 fine-tuning 을 위해서 pre-trained 가중치를 두 구성 요소 magnitude 와 direction 으로 분해하는데, 특별히 direction 업데이트를 위해서 LoRA 를 사용하여 훈련 가능한 파라미터의 수를 효율적으로 최소화 한다. DoRA 를 사용함으로써 추가적인 inference 의 오버헤드를 피하고 LoRA 의 훈련 안정성과 학습 능력 모두 향상 시킨다.

Overview

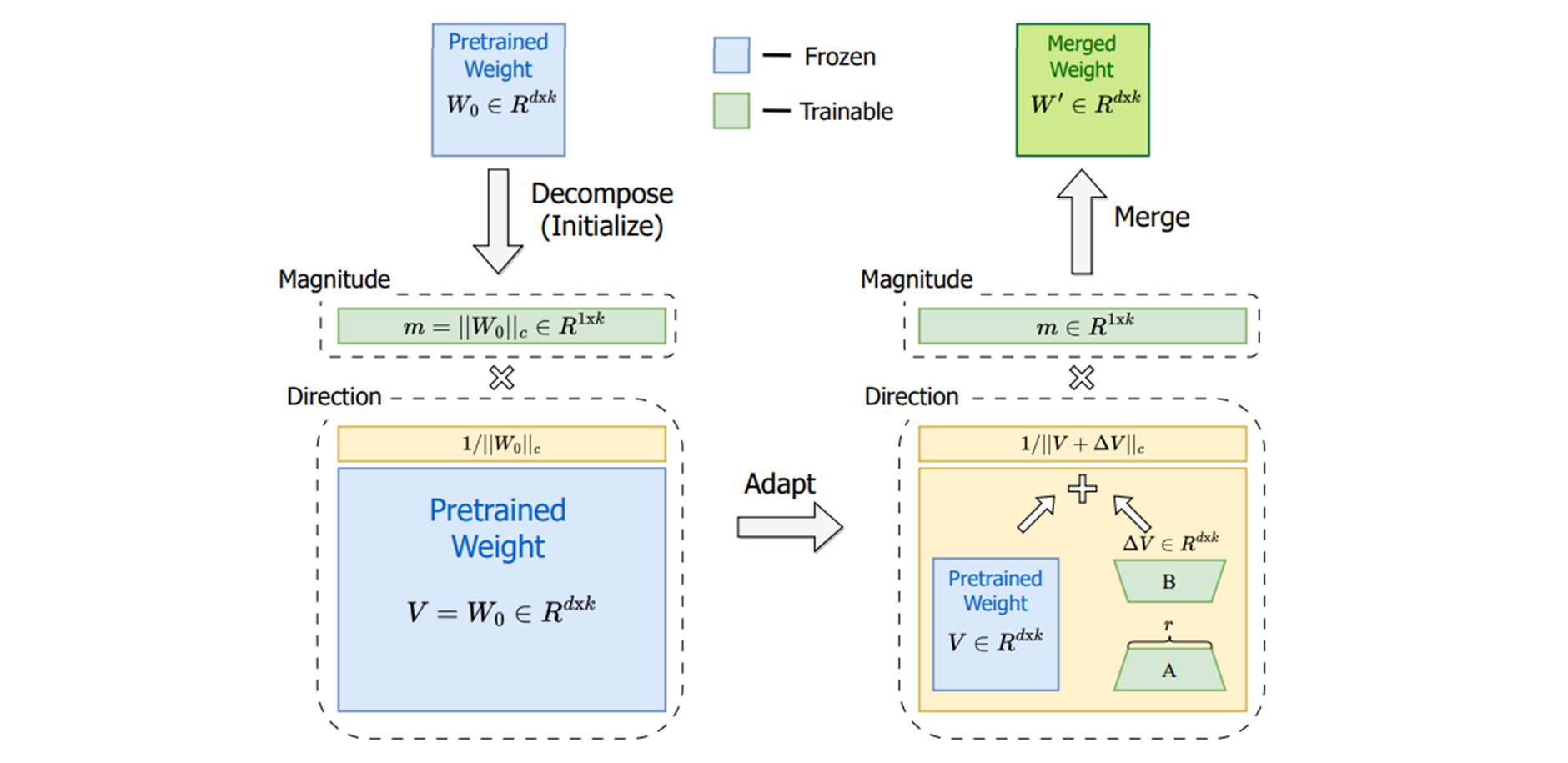
pre-trained 가중치를 fine-tuning 을 위해서 magnitude 와 direction 으로 분할하는데, 특히 LoRA 를 사용하여 direction 구성 요소를 효율적으로 업데이트 한다. $\Vert \cdot \Vert_c$ 는 각 열 벡터에 대한 행렬의 vector-wise norm 을 나타낸다.

Analysis Method

이 분석은 pre-trained 가중치에 관련되어 LoRA 와 Fine-Tune 의 magnitude 와 direction 모두 조사하여 두 가중치의 학습 행동들의 근본적인 차이를 나타낸다. 가중치 $W \in \mathbb{R}^{d\times k}$ 의 분할은

W = m \frac{V}{\Vert V \Vert}_c = \Vert W \Vert_c \frac{W}{\Vert W\Vert}_c

이로써 공식화 할 수 있다. 여기서 $m \in \mathbb{R}^{d \times k}$ 은 manitude vector 이고, $V \in \mathbb{R}^{d \times k}$ 는 directional matrix, $\Vert \cdot \Vert_c$ 는 각 열 벡터에 대한 행렬 vector-wise norm 이다. 이 분할은 $V / \Vert V \Vert_c$ 의 각 열은 단위 벡터로 유지되고, 각 벡터의 해당하는 스칼라 $m$ 은 각 벡터의 magnitude 로 정의한다.

Weight-Decomposed Low-Rank Adaptation

LoRA directional adaption 에만 집중하도록 제한하면서 크기의 구성 요소를 조정할 수 있도록 허용하면 원래의 접근 방식보다 작업이 단순화 된다. magnitude 와 direction 모두 조정을 학습하기 위해서는 LoRA 가 필요하다.
방향 업데이트를 최적화 하기 위한 프로세스는 weight decomposition 을 통해서 더욱 안정적으로 이루어 진다.

Weight normalization 은 magnitude 와 direction 구성 요소를 처음부터 ( from scratch ) 학습하여 다양한 초기화에 민감한 방법이지만, DoRA 는 이 두 구성 요소를 pre-trained weights 에서 시작하여 이와 같은 초기화 문제를 피한다.

magnitude $m = \Vert W_0 \Vert$ and $V = W_0$ 이후에 초기화 된다.
- keep $V$ frozen 이고 $m$ 은 trainable vector 가 된다.
- 초기에 모든 parameter 를 required_grad 를 False 로 둔 후 Frozen 시키고 $m$ 을 설정하면서 True 가 될 듯 하다.
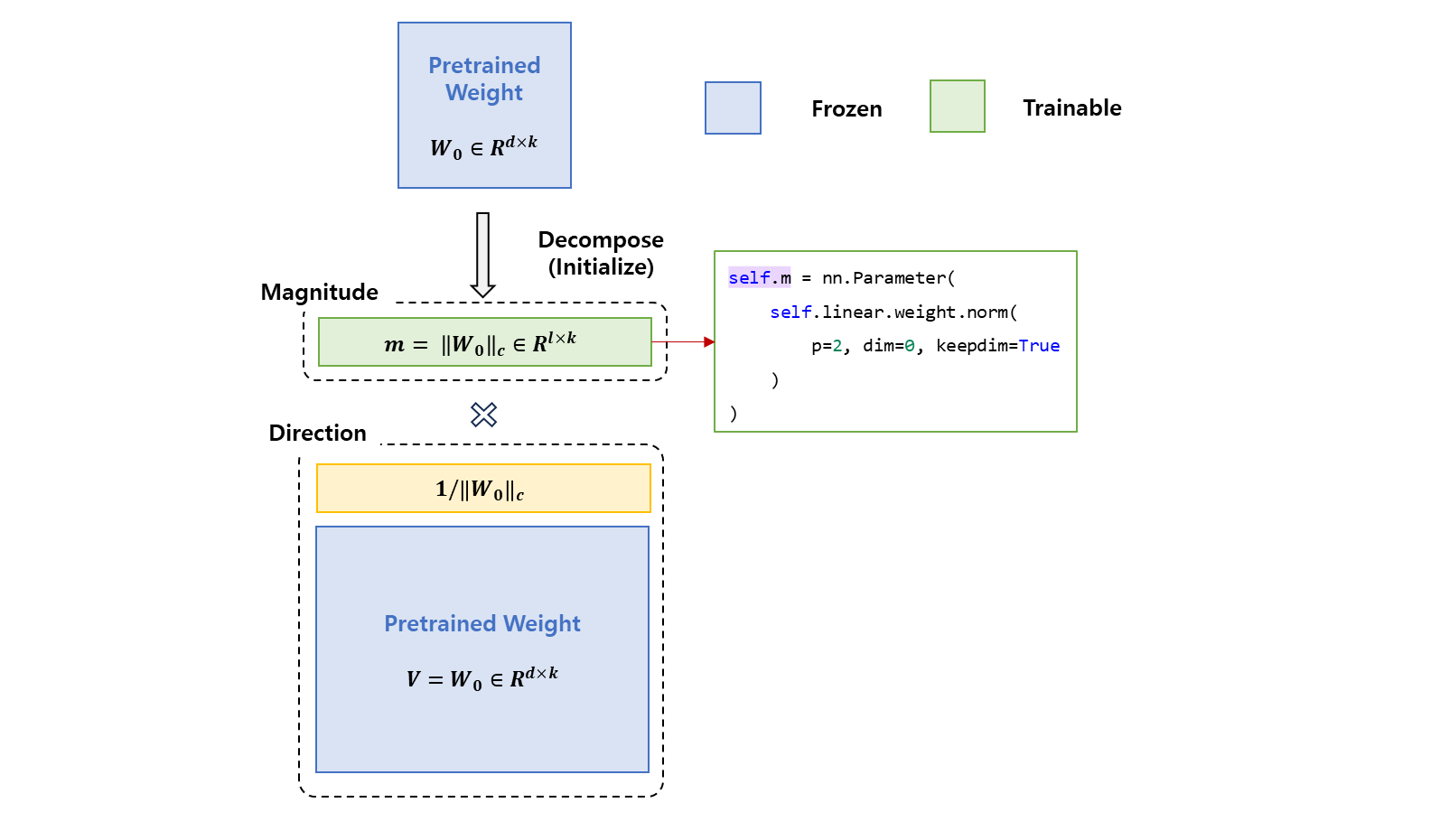
direction 구성 요소 설계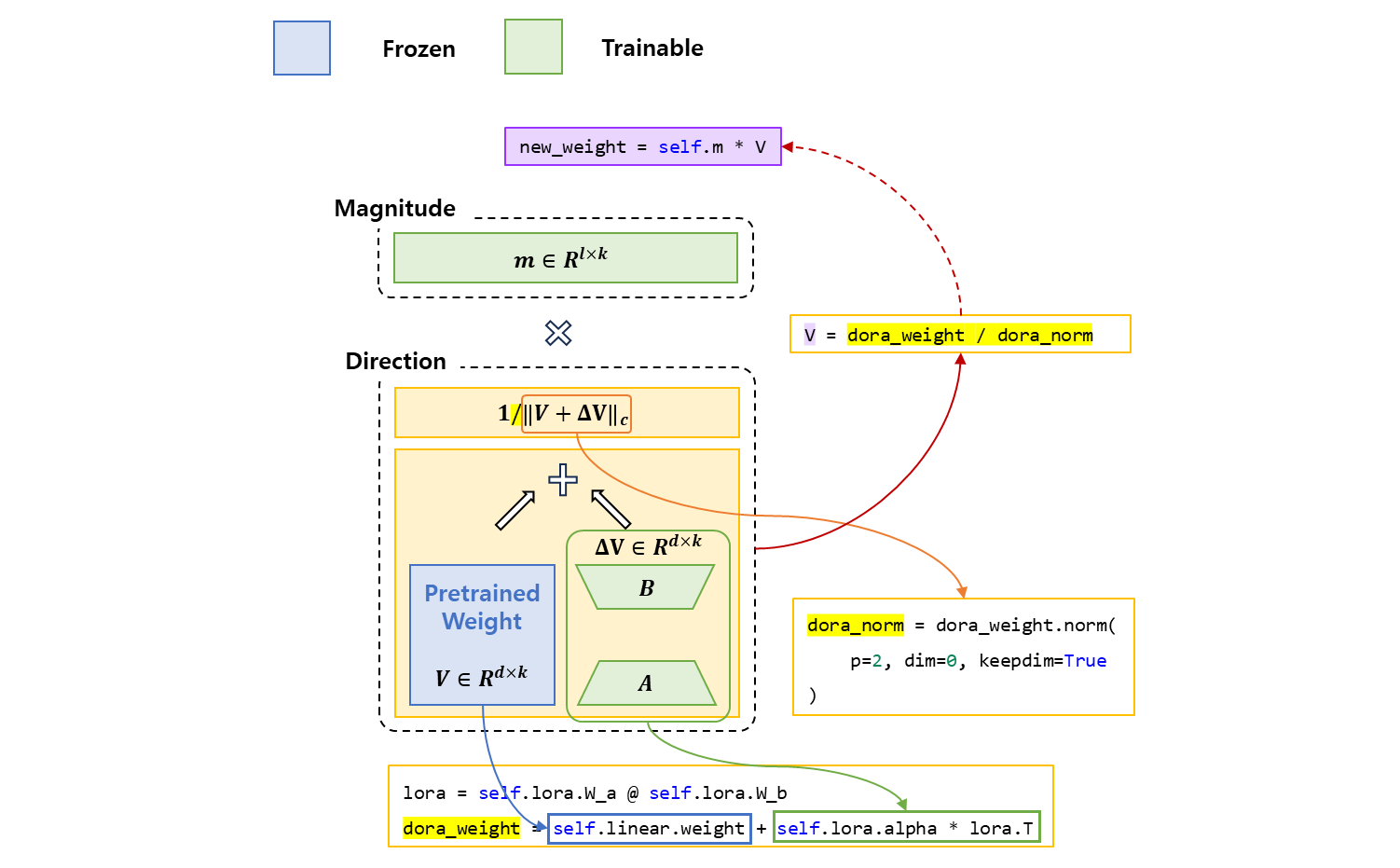
$W' = \underline{m}\frac{V + \Delta V}{\Vert V + \Delta V \Vert_c} = \underline{m}\frac{W_0 + \underline{BA}}{\Vert W_0 + \underline{BA} \Vert_c}$

$\Delta V$ 는 두 개의 low-rank $B, A$ 행렬를 곱하여 학습 후 더하는 directional 업데이트 이다.

code

class LinearWithDoRA(nn.Module):
    def __init__(self, linear, rank, alpha):
        super(LinearWithDoRA, self).__init__()
        self.linear = linear
        self.lora = LoRALayer(
            linear.in_features, linear.out_features, rank, alpha
        )

        # Magnitude
        self.m = nn.Parameter(
            self.linear.weight.norm(p=2, dim=0, keepdim=True)
        )

    def forward(self, x):
        # Direction
        lora = self.lora.W_a @ self.lora.W_b
        dora_weight = self.linear.weight + self.lora.alpha * lora.T

        dora_norm = dora_weight.norm(p=2, dim=0, keepdim=True)
        V = dora_weight / dora_norm

        new_weight = self.m * V

        return F.linear(x, new_weight, self.linear.bias)

Result

LoRA 는 pre-trained 된 다재다능한 범용적인 모델에, attention layer 등의 linear layer 에 나만의 task 데이터를 학습하여 더하여 지식 정보를 집어 넣는다고 보면 된다.
그러나 여기서 transformer 를 보면 positional encoding 을 사용하여 단어의 위치 정보를 갖는 것으로 학습하게 되는데, 저렇게 linear 속에 집어 넣으면 이 위치 정보들이 깨지는 것이 아닌가 생각이 들었다.
DoRA 도 마찬가지기는 하나, 독특한 것은 normalization 을 하여 direction 만 가져가서 미세하게 튜닝 시키고, 기존의 pre-training 된 데이터의 magnitude 를 사용하여 크기를 가져간다면, 관계가 없지 않을까? 라는 생각과
Llama 계열은 rotary position embedding 을 attention layer 에서 하므로 relative 하게 들어가므로, 좀 더 유연하면서 robust 하기 때문에 적합하지 않을까 한다. 현재 모델들은 이러한 방향으로 갈 듯 하다.