05. Policy Improvement

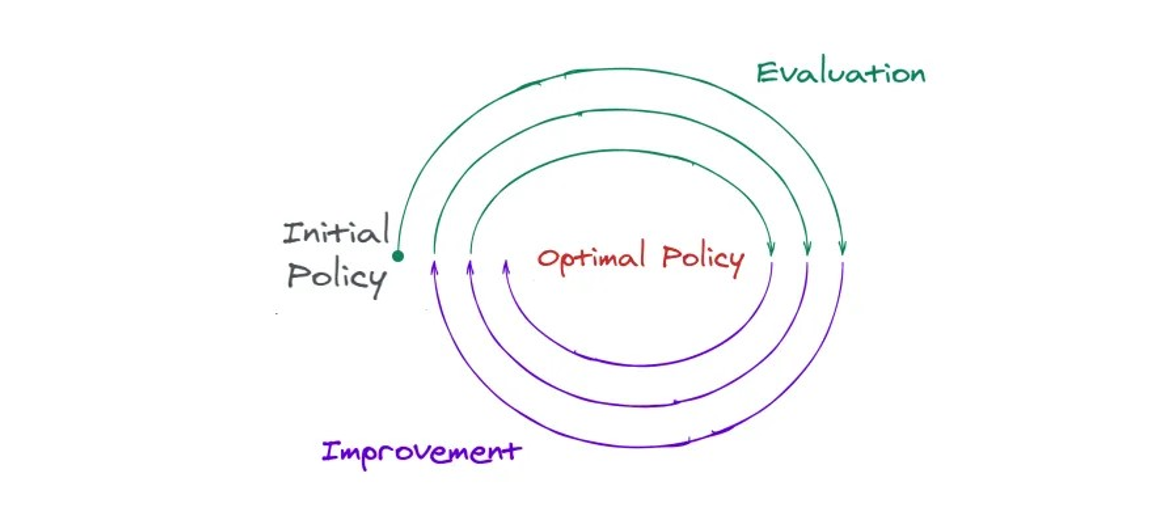
policy improvement

Policy 를 개선하는 방법을 말한다.

• 이 과정에서 Value $(V^{\pi})$ 또는 Action-Value $(Q^{\pi})$ function 의 policy 가 greedy 하게 바뀐다.

  • 각 function 들이 더 높은 행동을 많이 하도록 policy 를 바꾼다.
  • 각 function 들의 값에 의존하여 더 greedy 하게, 탐욕적으로 얻고자 하는 행동을 한다.

• $\pi$ 의 Action-Value function 을 알고 있다면..

  $\pi'(a|s) = \begin{aligned} &\begin{cases} 0.9 \cdot \pi(a|s) + 0.1 & {\rm if} \; a = \argmax_a Q^{\pi}(s,a) \\ 0.9 \cdot \pi(a|s) & {\rm else} \end{cases} \end{aligned}$

  더 나은 policy $(\pi')$ 를 얻을 수 있다.

  $\pi'$ : 새롭게 얻은 policy 이고, 기존 policy 에 $0.9$ 를 곱한 다음, $0.1$ 을 더하는 policy 이다.

  1. 주어진 state $(s)$ 에서 action value $(a)$ 값을 최대화 하는 행동에 대해서 update 하고, 그 외의 행동에 대해서는 $0.1$ 을 더하지 않겠다.

  2. 기존 $\pi$ 에 모두 $0.9$ 배가 되었으므로, 전체 합이 $0.9$ 가 되고, 나머지 $0.1$ 을 가장 큰 행동에 투자한 policy 이다.

check new policy is more greedy

새롭게 얻은 policy $\pi'$ 에 대해 기존 $Q^{\pi}$ 가 더 greedy 하게 바뀌었는지 보자.

• $\underline\text{new policy}$ $\pi'$ 의 $Q^{\pi}$ 의 평균 이 $\underline\text{original policy}$ $\pi$ 에서 $Q^{\pi}$ 를 평균 낸 것보다 더 크냐? 의 질문.

  $\sum_a \pi'(a|s) Q^{\pi}(s, a) \geq \sum_a \pi(a|s)Q^{\pi}(s,a) ?$

• 왼쪽이 더 크다면, $\pi'$ 은 $\pi$ 보다 $Q^{\pi}$ 에 대해서 더 greedy 하다고 볼 수 있다.

  $\sum_a \pi'(a|s) Q^{\pi}(s, a) - \sum_a \pi(a|s)Q^{\pi}(s,a) \geq 0$

• $\underline\text{new policy}$ $\pi'$ 는 $\underline\text{original policy}$ $\pi$ 에 $0.9$ 를 곱한 것에 $Q^{\pi}$ 를 최대화 하는 행동에 대해서만 $0.1$ 의 확률을 추가 한다.

  $\sum_a \pi'(a|s) Q^{\pi}(s, a) = \sum_a 0.9 \pi(a|s)Q^{\pi}(s, a) + \left[ 0.1 Q^{\pi}(s, a_{\max}) \right]$

• 이것을 풀어서 계산해보면,

  $\begin{aligned} 0.9\sum_a \pi(a|s)Q^{\pi}(s, a) + \left[0.1 Q^{\pi}(s, a_{\max})\right] - 1.0\sum_a \pi(a|s)Q^{\pi}(s,a) &\geq 0 \\ 0.1 Q^{\pi}(s, a_{\max}) - 0.1\sum_a \pi(a|s)Q^{\pi}(s,a) &\geq 0 \end{aligned}$
  • 왼쪽은 가장 큰 값에 $0.1$ 을 곱한 값.
  • 오른쪽은 모든 가능한 행동에 대한 $Q^{\pi}$ 에 대해 평균에 $0.1$ 을 곱한 값.

  따라서 그 차는 $0$ 이상이 된다

  $\sum_a \pi'(a|s) Q^{\pi}(s, a) \geq \sum_a \pi(a|s)Q^{\pi}(s,a) \rightarrow {\rm True}$

• $\pi'$ 가 $\pi$ 보다 $Q^{\pi}$ 에 대해서 더 greedy 하다는 것이 증명 되었다.

analyze new policy

• $Q^{\pi}$ ( Action-Value function ) 에 대해서 greedy 하게 개선된 policy 는 아래의 조건을 만족한다.

  $\sum_{a}\pi(a|s)Q^{\pi}(s, a) \leq \sum_{a}\pi'(a|s)Q^{\pi}(s, a) \; \text{for all} \; s\in \mathcal{S}$
  • 좌변은 $Q^{\pi'}$ 를 $\pi$ 에 대해서 평균 낸 것이다.
    • 새로운 policy ${\pi'}$ 에 대해서 평균을 취한 것 보다 작거나 같다.
  • 우변 $\pi'$ 를 모든 state 에서 다 update 했다면, 이 조건은 모든 state 에서 만족하게 된다.

• $Q^{\pi}(s, a)$ 를 policy $\pi(a|s)$ 로 평균 낸 값은,
  $\rightarrow$ state $s$ 에서 평균적으로 받는 return. 즉, $V^{\pi}$ ( Value function ) 이 된다.

  $\mathbb{E}^{\pi}_{a}\left[ Q^{\pi}(s, a)\right] = V^{\pi}(s) \leq \mathbb{E}^{\pi'}_{a} \left[ Q^{\pi}(s, a) \right] \; \text{for all} \; s \in \mathcal{S}$
  • $\mathbb{E}^{\pi'}_{a}[Q^{\pi}(s, a)]$ : $Q^{\pi}$ 를 가지고 정책을 greedy 하게 바꿔서, 평균 값이 더 커진다.
  • $V^{\pi}$ 이 $Q^{\pi}$ ( Action-Value function ) 를 $\pi'$ 에 대해서 평균 낸 것보다 작거나 같다.

• $Q^{\pi}$ 를 가지고 더 greedy 하게 바꾸었으므로, 그것에 대해서 평균 값이 더 커진다.

policy improvement theorem

그런데, 위 조건을 만족하면 $\pi'$ 이 $\pi$ 보다 더 좋은 policy 라고 할 수 있을까??

위의 조건을 만족하면 $\pi'$ 이 $\pi$ 보다 더 나은 policy 라고 할 수 있다.

• 모든 state 에서 $Q^{\pi}$ 는 Action $a$ 를 가지고
  $\text{for all} \; s \in \mathcal{S}$

  • $\pi'$ 에 대해서 평균을 낸 것이 $\pi$ 에 대해서 평균을 낸 것보다 크거나 같으면,
    $\mathbb{E}^{\pi}_{a}[Q^{\pi}(s, a)] \leq \mathbb{E}_{a}^{\pi'}[Q^{\pi}(s, a)]$

  • 모든 state 에서 $V^{\pi'}$ 가 $V^{\pi}$ 보다 크거나 같다.
    $V^{\pi}(s) \leq V^{\pi'}(s)$

• 위의 정보로 알수 있는 식은 $V^{\pi}(s_t) \leq \mathbb{E}^{\pi'}_{a_t} \left[Q^{\pi}(s_t, a_t) \right]$

  • $V^{\pi}(s_t)$ 는 $Q^{\pi}(s_t, a_t)$ 의 $\pi'$ 에 대해 평균 낸 것 보다 작거나 같다.
  • $\pi'$ 가 $Q^{\pi}$ 에 대해 더 greedy 하게 update 되었기 때문에 이는 모든 state 에 대해서 만족한다.
  • $\pi$ 에 대한 $Q^{\pi}(s_t, a_t)$ 는 action 과 state 는 정해졌으므로, 다음 transition 만 고려한다.

proof

$V^{\pi}(s_t) \leq \mathbb{E}^{\pi'}_{a_t} \left[Q^{\pi}(s_t, a_t) \right]$ 이것을 시작하자.

1. $\pi$ 에 대한 $Q^{\pi}$ 는 $V^{\pi}$ 를 이용해서 표현할 수 있다.

   $\begin{aligned} &Q^{\pi}(s_t, a_t)\\ &= \sum_{s_{t+1}}p(s_{t+1}|s_t, a_t) \left[ R(s_t, a_t, s_{t+1}) + \gamma V^{\pi}(s_{t+1}) \right] \\ &= \mathbb{E}_{s_{t+1}}\left[ R(s_t, a_t, s_{t+1}) + \gamma V^{\pi}(s_{t+1}) \right] \end{aligned}$

2. 풀어진 식을 대입하면

   $\begin{aligned} V^{\pi}(s_t) &\leq \mathbb{E}^{\pi'}_{a_t} \left[Q^{\pi}(s_t, a_t) \right] \\ &= \mathbb{E}^{\pi'}_{a_t, s_{t+1}}\left[r_{t+1} + \gamma V^{\pi}(s_{t+1}) \right] \; \text{with} \; r_{t+1} = R(s_t, a_t, s_{t+1}) \end{aligned}$

3. $V^{\pi}(s_t) \leq \mathbb{E}^{\pi'}_{a_t} \left[Q^{\pi}(s_t, a_t) \right]$ 이는 모든 state 에서 만족하므로

   $V^{\pi}(s_{t+1}) \leq \mathbb{E}^{\pi'}_{a_{t+1}} \left[Q^{\pi}(s_{t+1}, a_{t+1}) \right]$

   이 식도 만족하게 되어 그대로 대입하면,

   $\leq \mathbb{E}^{\pi'}_{a_{t:t+1}, s_{t+1}}\left[ r_{t+1} + \gamma Q^{\pi}(s_{t+1}, a_{t+1}) \right]$

   로 $a_t$ 였던 것이 $a_{t+1}$ 까지 추가된다.

4. $Q^{\pi}(s_{t+1}, a_{t+1})$ 을 풀어쓰면,

   $\begin{aligned} &Q^{\pi}(s_{t+1}, a_{t+1}) \\ &= \sum_{s_{t+2}}p(s_{t+2}|s_{t+1}, a_{t+1}) \left[ R(s_{t+1}, a_{t+1}, s_{t+2}) + \gamma V^{\pi}(s_{t+2}) \right] \\ &= \mathbb{E}_{s_{t+2}}\left[ R(s_{t+1}, a_{t+1}, s_{t+2}) + \gamma V^{\pi}(s_{t+2}) \right] \end{aligned}$

5. 이와 같은 방법으로 $a_t$ 에서 $a_{t+k}$ 까지 $k$ 번 풀어 쓰면,

   $\leq \lim_{k \rightarrow \infin} \mathbb{E}^{\pi'}_{a_{t:t+k},s_{t+1:t+k}} \left[ r_{t+1} + \gamma r_{t+2} + \gamma^2r_{t+3} + \cdots + \gamma^{k-1}r_{t+k} + \gamma^{k}Q^{\pi}(s_{t+k}, a_{t+k})\right]$
   • $\gamma^{0}$ 에서 $\gamma^{k-1}$ 까지, $r_{t+1}$ 에서 $r_{t+k}$ 나올 것, 마지막 항에 $\gamma^{k}Q^{\pi}$ 가 나온다.
   • $\gamma < 1$ 이면 $\gamma^{k}Q^{\pi}(s_{t+k}, a_{t+k}) = 0$ 이 되고,
   • 나머지 나열되는 식은 $\pi'$ 에 대해서 이 값을 평균 내고 있으므로 $V^{\pi'}(s_t)$ 가 된다.
   • $\pi'$ 를 따라 행동 했을 때 평균적으로 받는 return 은 $V^{\pi'}(s_t)$ 이다.

6. 전체는 아래와 같다.

   $\begin{aligned} V^{\pi}(s_t) &\leq \mathbb{E}^{\pi'}_{a_t} \left[Q^{\pi}(s_t, a_t) \right] \\ &= \mathbb{E}^{\pi'}_{a_t, s_{t+1}}\left[r_{t+1} + \gamma V^{\pi}(s_{t+1}) \right] \; \text{with} \; r_{t+1} = R(s_t, a_t, s_{t+1}) \\ &\leq \mathbb{E}^{\pi'}_{a_{t:t+1}, s_{t+1}}\left[ r_{t+1} + \gamma Q^{\pi}(s_{t+1}, a_{t+1}) \right] \\ &=\mathbb{E}^{\pi'}_{a_{t:t+1},s_{t+1:t+2}}\left[r_{t+1} + \gamma r_{t+2} + \gamma^2V^{\pi}(s_{t+2})\right] \\ & \quad\quad\quad\quad\quad\quad\quad \vdots \\ &\leq \lim_{k \rightarrow \infin} \mathbb{E}^{\pi'}_{a_{t:t+k},s_{t+1:t+k}} \left[ r_{t+1} + \gamma r_{t+2} + \gamma^2r_{t+3} + \cdots + \gamma^{k}Q^{\pi}(s_{t+k}, a_{t+k})\right] \\ &= V^{\pi'}(s_t) \end{aligned}$

7. $\left[V^{\pi}(s) \leq V^{\pi'}(s) \; \text{for all} \; s \in \mathcal{S}\right]$

   • $V^{\pi'}(s_t)$ 는 $V^{\pi}(s_t)$ 보다 모든 state 에 대해서 항상 크거나 같다.
   • 모든 state 에서 $\pi'$ 을 통해서 얻을 수 있는 value 가 더 크다는 것은 $\pi'$ 이 $\pi$ 보다 더 나은 policy 라는 것을 의미한다.

8. 결론
   Policy Improvement theorem 에 의해서 $Q^{\pi}$ 혹은, $V^{\pi}$ 에 대해서 더 greedy 하게 policy 를 update 하면, 그 policy 는 더 나은 policy 가 된다. 이 말은 $Q^{\pi}$ 혹은, $V^{\pi}$ 만 가지고 강화를 해도 된다.

find optimal policy

• policy improvement 를 이용해서 optimal policy 를 찾을수 있는가?

  $\pi_{k+1}(a|s) = \begin{aligned} &\begin{cases} 1 & {\rm if} \; a = \argmax_a Q^{\pi_k}(s,a) \\ 0 & {\rm else} \end{cases} \end{aligned}$
  • improvement 를 거칠 때 마다, 위와 같은 policy 를 얻게 된다고 가정.
  • $\pi_{k+1}(a|s)$ 는 기존 $\pi_k$ 에 의한 $Q^{\pi_k}$ 중에 가장 좋은 행동 $(\argmax_a)$만 $1$ 의 확률로 바꾸는 것.
  • 가장 좋은 것만 $100\%$ 로 고를 수 있게 바꾸는 것.

• 이렇게 policy 를 계속 update 하면, policy improvement theorem 에 의해 모든 state 에 대해서 $V^{\pi}$ ( Value ), $Q^{\pi}$ ( Action-Value ) function 이 개선된다.

• $V^{\pi}$ 이 계속 개선되다가 $\pi$ 에 따르는 정해진 value 에 어느 정도 수렴하게 될텐데, 이 Improvement 가 수렴했을 때는 $V^{\pi_k} = V^{\pi_{k+1}}$ 이 모든 state 에 대해서 동일 하겠다.

  $\lim_{k \rightarrow \infin}V^{\pi_k}(s) = V^{\pi_{k+1}}(s) \; \text{for all} \; s \in \mathcal{S}$

bellman optimality equation.

• 여기서 $V^{\pi_k}$ 를 Bellman equation 식을 이용해서 써보면

  $V^{\pi_k}(s) = \sum_a\sum_{s'}p(s'|s,a)\pi_{k}(a|s)(r + \gamma V^{\pi_{k}}(s'))$

  인데, $V^{\pi_k} = V^{\pi_{k+1}}$ 이므로 $V^{\pi_{k+1}}$ 에 대한 Bellman equation 을 써도 무방하다.

  $V^{\pi_k}(s) = \sum_a\sum_{s'}p(s'|s,a)\pi_{k+1}(a|s)(r + \gamma V^{\pi_{k+1}}(s'))$

  그리고 $V^{\pi_{k+1}}$ 만 $V^{\pi_k}$ 로 바꿔주면,

  $V^{\pi_k}(s) = \sum_a\sum_{s'}p(s'|s,a)\pi_{k+1}(a|s)(r + \gamma V^{\pi_{k}}(s'))$

  $\pi_{k+1}$ 은 $\pi_k$ 에 대한 $Q^{\pi}$ 의 max operator 로 바뀔 수 있다.

  $\pi_{k+1}(a|s) = \begin{aligned} &\begin{cases} 1 & {\rm if} \; a = \argmax_a Q^{\pi_k}(s,a) \\ 0 & {\rm else} \end{cases} \end{aligned}$
  • $\pi_{k+1}$ 에 대한 action 은 $\pi_{k}$ 에 대한 $Q^{\pi_k}$ 값 중에서 가장 큰 것만 $100\%$ 고르기 때문.
  • $\pi_{k}$ 에 대한 $Q^{\pi_k}(s,a)$ 에서 가장 크게 하는 행동이 $\pi_{k+1}$ 이므로 ${\rm max}$ operator 로 바뀔 수 있다.
  $V^{\pi_k}(s)=\max_a \sum_{s'}p(s'|s,a)(r + \gamma V^{\pi_k}(s'))$

  이것은 Bellman optimality equation! 이다.

result

• $V^{\pi_k}$ 가 Bellman optimality equation 을 만족한다는 것인데
  • optimal value function 이라는 뜻.
  • $\pi_k$ 는 optimal policy 중 하나라는 뜻.
    • optimal policy 는 여러 개가 될 수 있다.
• 최종적으로 얻은 식은 Bellman optimality equation 이고,
  $V^{\pi_k}(s) = \max_a \sum_{s'}p(s'|s,a)(r + \gamma V^{\pi_k}(s')) \; \text{for all} \; s \in \mathcal{S}$
  • 이 policy 를 모든 state 에 대해서 계속 update 를 하면, optimal policy 를 얻을 수 있다.
  • $V^{\pi_k}(s)$ 는 optimal value function 이고, 따라서 $\pi_k$ 는 optimal poilcy 이다.

ref

• thumbnail image.
  https://towardsdatascience.com/policy-and-value-iteration-78501afb41d2