06. Policy Iteration

policy iteration

• Policy Evaluation 과 Policy Improvement 의 반복된 과정을 말한다.

$\quad PE : \text{Policy Evaluation},\quad PI : \text{Policy Improvement}$

• 이 반복되는 과정을 policy iteration 이라고 한다.

  1. policy $(\pi_0)$ 에서 시작하여
  2. policy evaluation 을 통해 policy 의 value function $(V^{\pi_0})$ 을 찾고,
  3. Value function 을 활용해서
  4. Policy Improvement 를 통해 $(\pi_{1})$ 을 얻은 다음에
  5. 다시 Policy Evaluation 과정을 계속해서 반복하다 보면,
  6. 결국 Optimal Policy $(\pi_*)$ 와 Optimal Value function $(V^{\pi_*})$ 을 얻게 된다.

step description

• policy evaluation 과 policy improvement 를 활용해서 policy iteration 알고리즘을 만들 수 있다.

  1. Value function $V^n$ 이 더 나아지다가,
  2. optimal value function 에 가까워지면, 그 차이 값이 점점 줄어들게 된다.
  3. 이 value function 이 optimal value function 에 수렴했는지의 여부로써, $\Delta$ 를 이용.
  4. 이 $V^n$ 의 변화량이 점점 줄어들면, optimal value function 에 수렴했다고 가정, 멈춘다.

1. initialize

• $\pi(\cdot \mid s)$ and $V(s)$ for all $s \in \mathcal{S}$

  모든 state 에 대해서 임의의 Policy 와 임의의 Value function 을 만든다.

2. policy evaluation

임의의 policy 에 policy evaluation 을 진행한다.

---

set $V_0 = V, \delta > 0, \Delta = \delta$ and $k = 0$
while $\Delta \geq \delta$
set $\Delta = 0$
  for $s \in \mathcal{S}$
    $V_{k+1}(s) = \sum\limits_a \sum\limits_{s'}p(s'\mid s, a)\pi(a \mid s) \left[ R(s, a, s') + \gamma V_k(s') \right]$
    $\Delta = \max \left( \Delta, |V_{k+1}(s)-V_k(s)|\right)$
  $k = k + 1$

---

3. policy improvement

initialize value func.

set $\Delta = 0$

• value function 이 optimal value function 로 수렴하는지 그 여부를 판별하기 위해 $\Delta = 0$ 으로 설정.

calculate 1st value func.

for $s \in S$
  $\Delta = \max(\Delta, |V_k(s) - V(s)|)$

• 모든 state 에 대해서 새로 계산한 value function

  • $V_{k}$ 는 방금 전 policy evaluation 을 통해서 얻은 value function.
  • $V_{k}$ 를 얻기 전의 value function $V$

• 이 2개 사이의 차이 중에 가장 큰 것을 $\Delta$ 에 저장한다.

이렇게 모든 state 에 대해서 이 과정을 거치면, 차이 값 중에 가장 큰 것만 저장된다.

compare threshold, update value func.

if $\Delta > \delta$
  $V = V^{k}$
  for $s \in S$
    $a_{\max} = \argmax\limits_{a} \sum\limits_{s'}p\left(s'|s, a\right)\left[r + \gamma V(s') \right]$
    $\pi'\left( a_{\max} \mid s\right) = 1$
  $\pi = \pi'$
  go to 2. policy evaluation

• threshold 로 정한 $\delta$ 값을 $\Delta > \delta$ 이라면,
  • value function 이 optimal value function 에 아직 수렴하지 않았다고 판단.
  • 그 다음 improvement 를 진행한다.

1. $V = V^{k}$ 로 설정

2. 모든 state 에 대해서 이 과정을 다 거친 후

   • action-value 값은 $r+ \gamma V(s')$ 에 대해서 $s'$ 가지고 평균 낸 값 중
   • 가장 큰 action 을 $a_{\max}$ 라고 정하고,
   • $a_{\max}$ 에 대해서만 확률 값이 $1$ 이 되도록, 이 외에 나머지는 전부 $0$ 이 된다.
   • 이와 같이 새로운 policy $\pi'$ 로 만든다.

3. $\pi = \pi'$ 으로 설정 policy evaluation 가서 다음 $V_k$ 를 얻는다.

4. evaluation 을 거치고 나서 얻은 $V_k$ 로 비교하여 수렴하지 않았으면 iteration.

convergence

else
return $V$ and $\pi$

• 수렴 하였으면 optimal value function $V$ 와 policy $\pi$ 를 return 한다.

algorithm

policy evaluation 에서 얻은 value function 을 가지고 policy improvement 를 진행한다.

---

set $\Delta = 0$
for $s \in S$
  $\Delta = \max(\Delta, |V_k(s) - V(s)|)$
if $\Delta > \delta$
  $V = V^{k}$
  for $s \in S$
    $a_{\max} = \argmax\limits_{a} \sum\limits_{s'}p\left(s'|s, a\right)\left[r + \gamma V(s') \right]$
    $\pi'\left( a_{\max} \mid s\right) = 1$
  $\pi = \pi'$
  go to 2. policy evaluation
else
  return $V$ and $\pi$

---

policy iteration 은 policy evaluation 과 policy improvement 가 계속해서 반복되는 구조.

• policy evaluation 은 수렴하기 위해서 보통 여러 step 을 반복한다.

  • $V^{\pi}$ 를 찾기 위해서 $V^{k}$ 의 $k$ 가 반복되서 증가
  • 설정한 $\delta$ 이하로 value 값의 변화량이 떨어질 때 까지 계속해서 반복

이 policy evaluation 을 짧게 (k-step) 만 하면서 policy improvement 를 하여 시간을 줄이자.

• policy evaluation 을 수렴할 때 까지 하는 것이 아니라,
• k-step 만 짧게 해서 policy improvement 를 반복 해도, 최종 결과는 보통 같게 된다.
• optimal policy $\pi_*$ , optimal value function $V^{*}$ 을 얻는다.

generalized policy iteration

• 임의의 policy evaluation, policy improvement 알고리즘을 활용하여 policy iteration 을 진행하는 방법.

  • 다양한 알고리즘과 방법이 존재. 그 중 어떤 방법을 사용하던지
  • $V^{\pi}$ 를 찾기만 한다면, 더욱 greedy 한 policy 를 만들기만 한다면

이 과정을 무한히 반복했을 때,

• 결과적으로 optimal policy 와 optimal value function 을 얻는다.

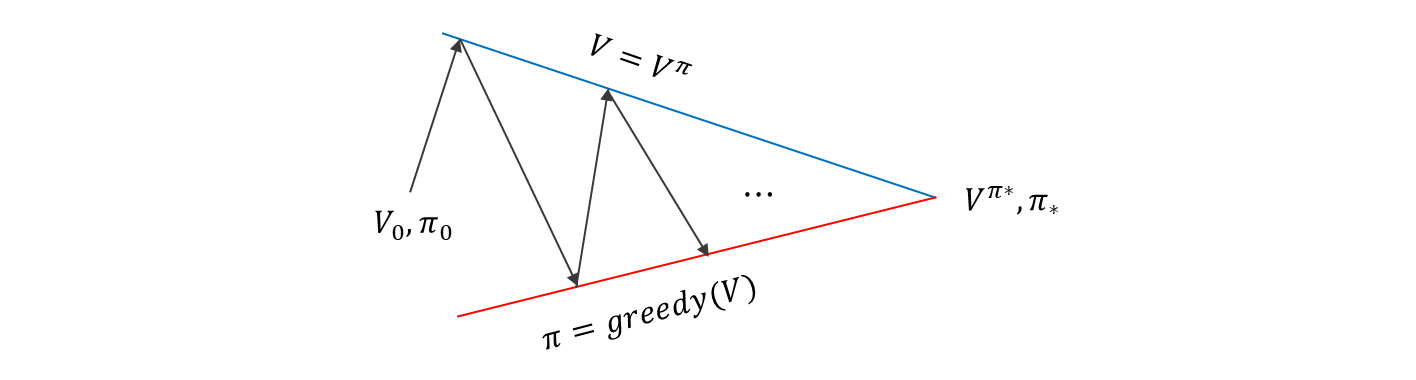
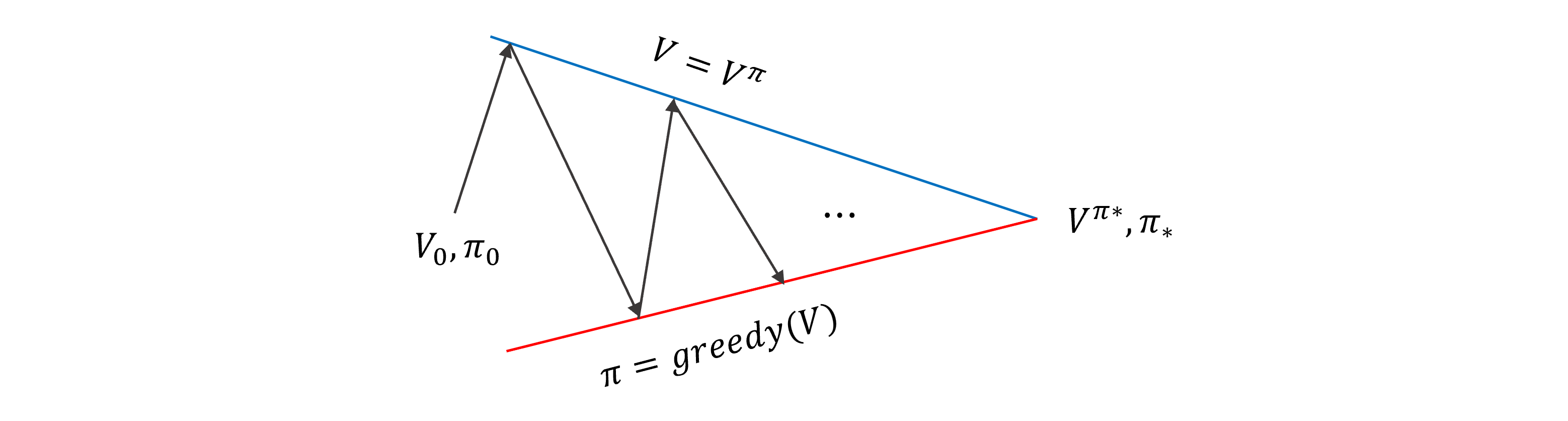
이 과정을 다르게 살펴보면,

• 임의의 $\pi$ (policy) 와 임의의 $V$ (value-function) 의 초기화가 random 이다.

• $V_0, \pi_0$ 부터 시작해서

  • policy evaluation 을 하면 $V^{\pi}$ 를 얻게 된다.
  • 빨간선은 어떤 value function 에 대한 greedy policy 의 점들을 나타낸 것
  • 파란선은 어떤 주어진 policy $\pi$ 에 대한 value function 에 점을 나타낸 것

여기서 직선으로 표현했지만, 실제로는 훨씬 더 복잡한 형태가 되겠지..

conclusion

policy iteration을 계속 반복하다가, 파란선과 빨간선이 만나는 지점 optimal value-function 과 optimal policy 로 가게 된다.

• policy evaluation : 임의의 policy evaluation 알고리즘을 사용하여 $V^{\pi}$ 로 추정.
• policy improvement : 임의의 policy improvement 알고리즘을 사용하여 $\pi^{'} \geq \pi$ 를 생성.

generalized policy iteration

• policy evaluation 과 임의의 policy improvement 를 계속 반복하는 과정
• 대부분의 강화학습 알고리즘이 이 개념으로 표현 된다.