[ Math of AI ] 1. transformer

d4r6j·2024년 5월 16일

목록 보기

3/3

조건희 교수님 늘 감사드립니다.

transformer structure

자연어, 이미지, 비디오 등등의 여러 분야의 기계학습에서 ‘self-attention’ 모델은 17 년도의 ‘Attention is All you Need’ 논문 이후에 매우 빈번히 사용된다. 트랜스포머의 구조를 수학적으로 살표본 후에 자연스러운 기하학적 관점으로 생각해보자.

트랜스포머의 수학적 구조 Query, Key and Value (Q, K, V)

Sentence example : DL is fun

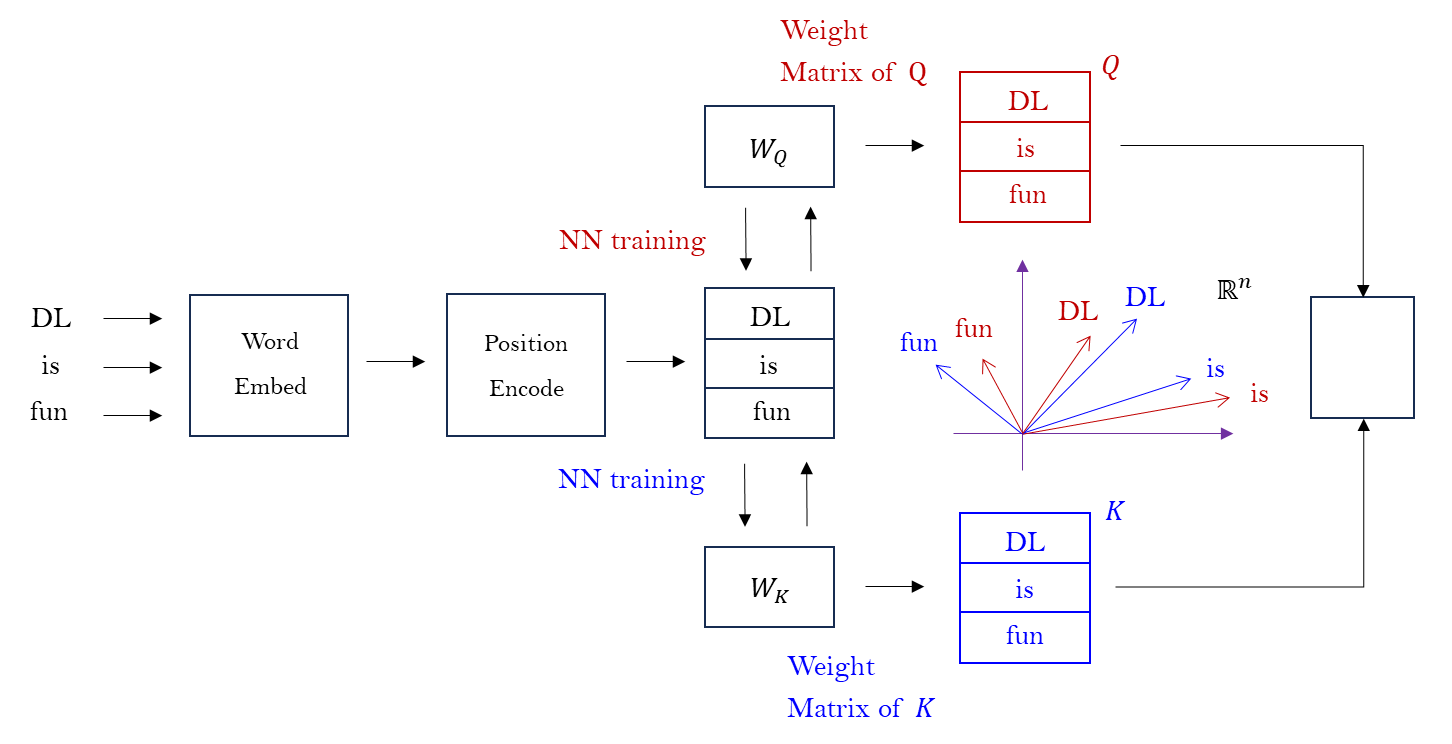
DL is fun 이 문장을 word embedding 으로 vector 로 바꾼다.
이 문장에서 단어들이 자리를 잡고 있는 ordering 을 position encode 로 주고,
weight matrix $(W_Q, W_K)$ , NN 을 학습하는 matrix 로 똑같은 문장에 대해서 다른 쪽으로 분기,
학습을 하여 DL is fun 이 문장을 다시 만든다. 실제로는 vector 로 표현 되어 있다.
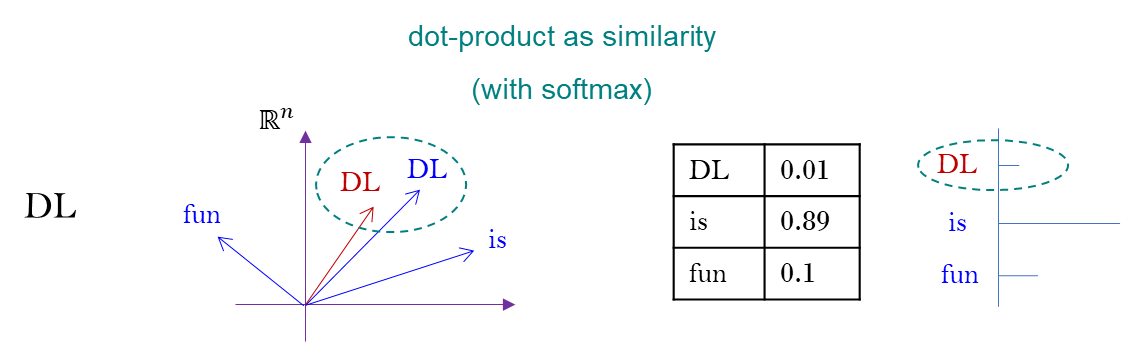
이 matrix 를 각각 두 개로 만들어서 그것을 합치는 과정에서 dot-product 를 사용한다.

Transformer 는 dot-product 를 사용하여 $Q$ 와 $K$ 의 유사도를 잰다.

step by step process

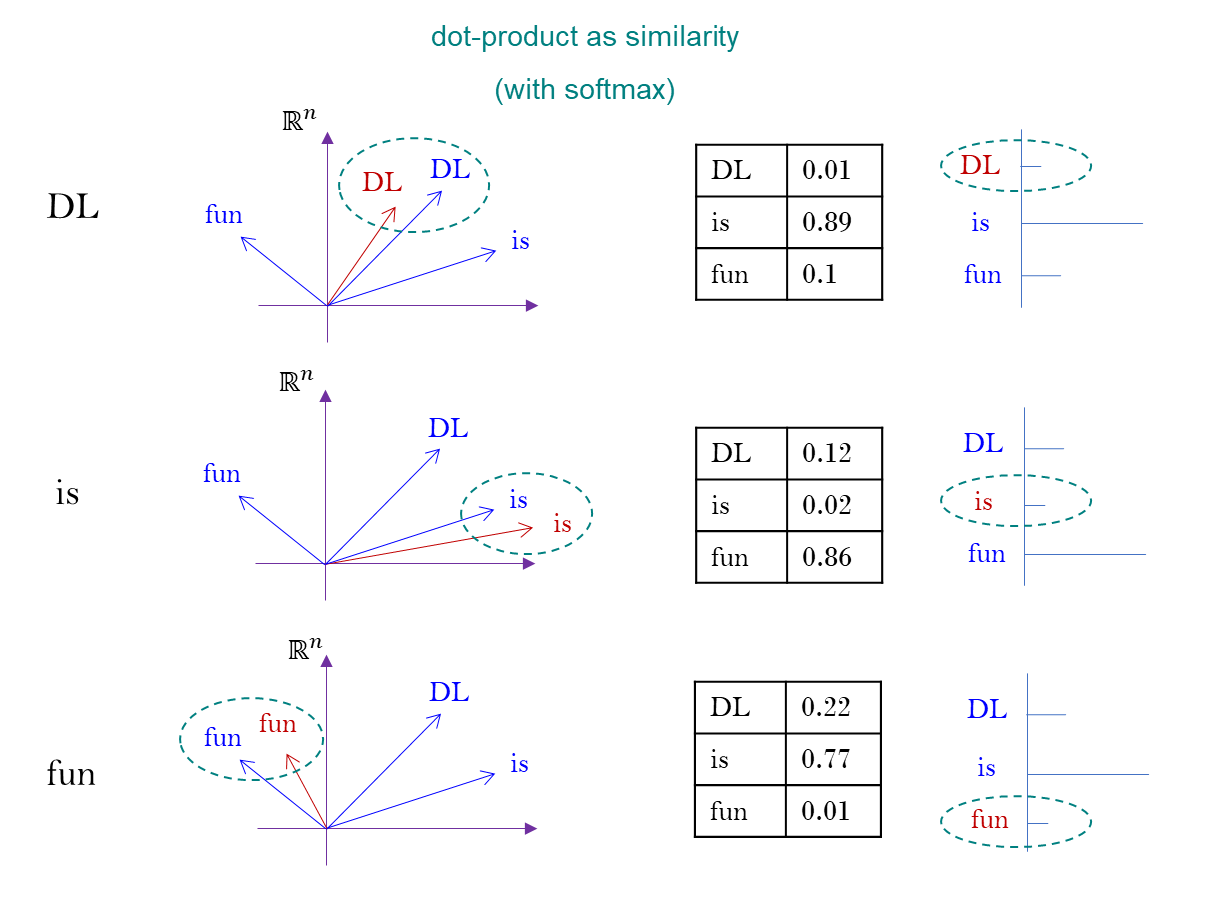
DL is fun 이 문장을 word embedding 으로 vector 로 바꾼다.
$\mathbb{R}^{n}$ 의 vector 로써 표현이 되어 있다.
이 문장 각각을 matrix 를 곱해서 만들겠다고 했다.
Query, Key 로 나누어서 볼 수 있는데, dot-product 면 그 각도를 잴 수 있다.
(inner-product) 는 magnitude 와 angle 을 규정한다.
softmax 를 취해서 총 합의 크기가 1이 되게 만들어 준다.
이 word 마다 기준의 vector 를 토대로
a. dot-product 를 기준으로 angle 을 재고,
b. 총 크기가 1이 되도록 맞추어 주면
이런 값들 (확률 정보) 의 결정이 가능하다.

문장 DL is fun 을 이해하려고 했을 때, 각각 서로가 어떻게 관계를 맺고 있는지를 규정하고자 하는 것이 이 값들을 부여하는 방식이다.

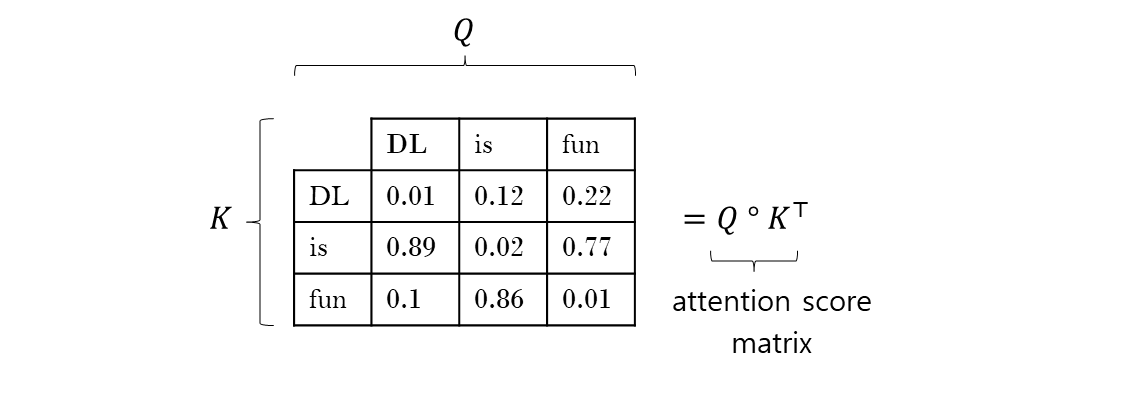
matrix 의 곱 이므로 dot-product 를 취한다. 여기에 Value matrix 를 하나 더 만들어서

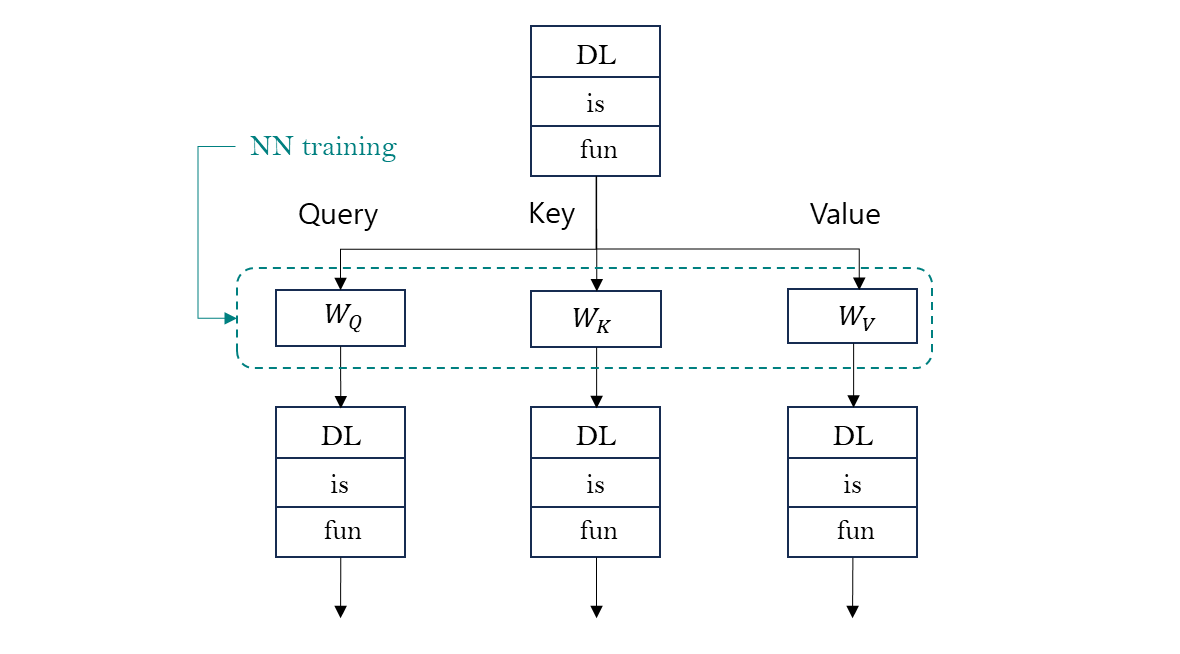
Attention(Q, K, V) = softmax\left( \frac{Q\cdot K^{\top} + Mask}{\sqrt{Embedding \;size}}\right)V

heuristic 하게 조정하고, masking 처리도 하지만 실제로 attention 이 하는 일이다.

Sentence 가 있으면 vector 처리를 하고
$W_Q, W_K, W_V$ 의 Weight matrix 를 만들고, 구하는 과정에서 Neural-Net 학습이 일어난다.
이 Weight matrix 를 곱해서 $Q, K, V$ 를 만든 다음,
위의 과정으로 encoder, decoder 든 업데이트 한다.

Attention 방법은 문장에서 DL is fun 서로가 어떻게 기여하고 있는지, clever 하게 섞어서 만들어 내는 방법이다.
Query, Key 를 분기해서 서로 맺고 있는 관계 (dot-product as similarity) 를 기준으로 만들어서 이 effect 를 $V$ alue 에 추가해서 실제로 이들이 어떻게 꼬여 있는 지를 반영하도록 하는 것이다.
같은 문장을 세 개로 분기하고, 곱하는 matrix 에 학습을 시키고, Query, Key, Value 를 다시 섞고 곱해서 다시 재구성 하는 것, 그러나 처리하는 과정에서 (dot-product) 를 쓰고 있는 부분에 오류가 있다.

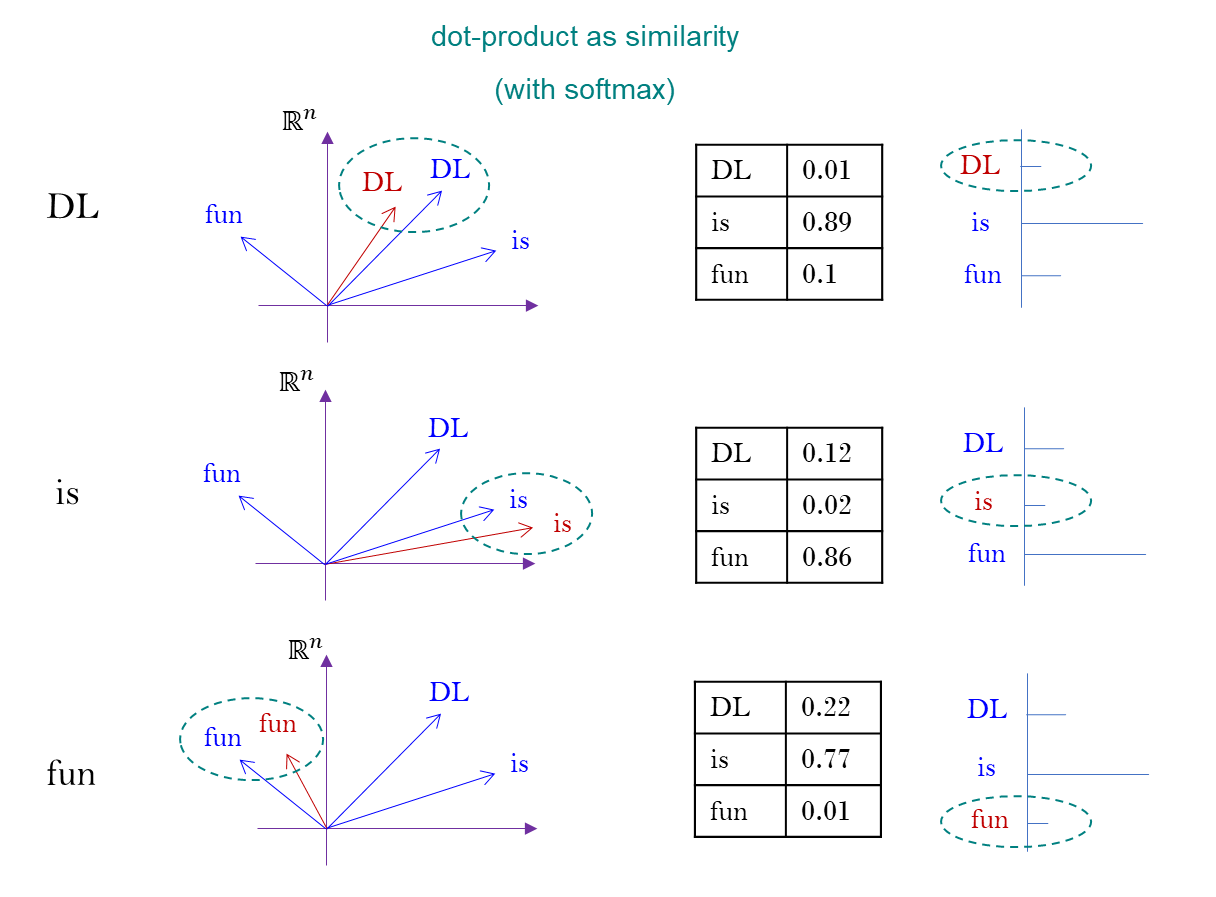
critical view

각각의 문장들과 단어들을 $\mathbb{R}^{n}$ 의 vector 들로 여기고 값을 부여하는 방식에서 dot-product 를 사용하고 있다. attention 포함 cosine similarity 또한 마찬가지로 볼 수 있다. Neural-Net 전반적인 dot-product 사용에 관한 모든 부분에 대한 다른 관점의 견해이다. 나 또한 동의하는 부분이다.

Attention(Q, K, V) = softmax\left( \frac{Q\cdot K^{\top} + Mask}{\sqrt{Embedding \;size}}\right)V

Cosine \; Similarity = \frac{A \cdot B}{\Vert A \Vert \; \Vert B \Vert} = \frac{\sum^{n}_{i=1}A_i \times B_i}{\sqrt{\sum^{n}_{i=1}(A_i)^2} \times \sqrt{\sum^{n}_{i=1}(B_i)^2}}

gradient vector 의 정의 까지 가는 이야기이다. 여기서 gradient vector 는 편미분 component vector 를 모은 것이 아니다. ( 참고 사항 ).

기하학적 관점에서 큰 비약이 있다.

thinking about dot-product

transformer 가 동작하는 대전제 부터 다시 한 번 생각해 봐야 한다.

DL is fun 각각의 단어들을 word embedding 을 사용하여 $\mathbb{R}^n$ 의 vector 로 바꾼다. 다음 유사도와 같은 방법을 사용하여 이런 식으로 재는 행위에 대해서 단어 및 문장들을 유클리드 공간의 $\mathbb{R}^{n}$ 의 vector 및 matrix 로 ‘잘’ 표현 되어야 한다.
수학은 집합과 함수를 이야기 하고 거기에 어떤 구조가 부여되는지를 헤아리는 것에서 통찰력을 얻어서 이해를 하고자 하는 것이다. 그러면 집합으로써는 DL is fun 의 모임이다. 이것을 $\mathbb{R}^{n}$ 의 vector 로써 여기고 있다. 단순히 “집합” 만으로 설명하지 못한다. 그러면 이것은 어떤 집합의 어떤 구조로 보고 있는지 이야기 해야한다.
그러면 사용하고 있는 것을 근거를 이야기 해야 하는데, dot-product 를 사용하고 있다. 어떠한 데이터를 $\mathbb{R}^n$ 의 원소로 바꾸었다고, $\mathbb{R}^n$ 의 구조, vector space 의 구조를 사용하는 것이 아니다. 그럼에도 불구하고 dot-product 는 써야한다. 이 단어들의 모임을 집합으로써는 manifold 구조 로 보고 있다. 그렇지 않고는 inner-product 를 이야기 할 수 없다.
이 알고리즘이 동작을 하려면, $\mathbb{R}^n$ 으로 보내서 inner product 로 보내야 하고, 각도가 정의되어야 하는 집합이어야 한다. 각도가 정의되는 집합을 다양체 (manifold) 라고 부르기로 했다. 이 의미는 $\mathbb{R}^n$ 에 집어넣겠다는 것이지, $\mathbb{R}^n$ 전체를 생각하겠다는 의미는 아니다.

manifold, metrics

$S^2$ 를 $\mathbb{R}^3$ 에 넣는 것, $\mathbb{H}^2$ 를 $\mathbb{R}^2$ 처럼 집어넣어 놓고, 거기서 무언가를 재고 있는 행위인데 여기서 문제의 포인트는 $\mathbb{R}^n$ 은 전체 집합에 대한 의미이다. 그렇다면 DL is fun 이 $\mathbb{R}^n$ 이 아니다.

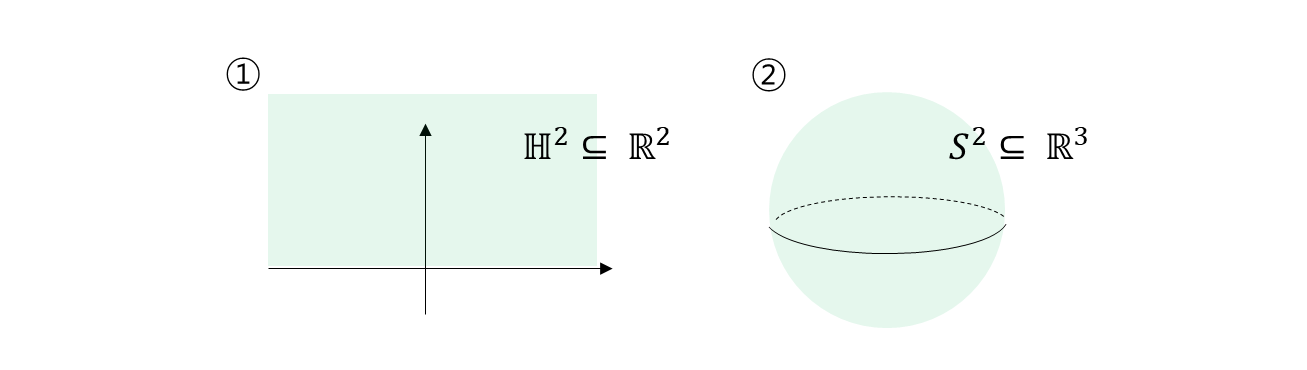
$\mathbb{H}^2$ 의 inner product 는 $\mathbb{R}^2$ 의 inner product 가 아니다. 그러면 $\mathbb{R}^2$ 의 inner product 를 $\mathbb{H}^2$ 에 쓰면 $\mathbb{H}^2$ 의 structure 와 안어울리게 된다. 그러면 그 부분만큼 문제가 된다.

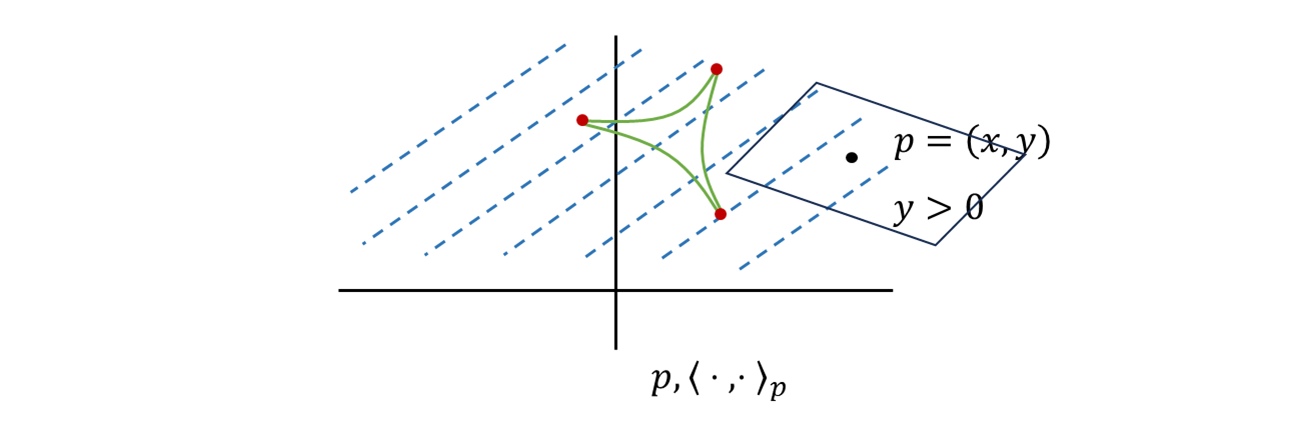
\langle \cdot, \cdot \rangle_p = \frac{1}{y^2} \left [ \begin{array}{c} 1 & 0 \\ 0 & 1 \end{array} \right ] := \rm{Poincar\acute{e} \; metric}

inner product

transformer NLP 영역에서 다루고자 하는 집합은 DL is fun 들의 모임이다. 문장들을 어떻게 볼 것이냐가 관건이다. 이러한 집합을 다루기 위해서, transformer 알고리즘이 동작하기 위해서, 일단 $\mathbb{R}^n$ 의 원소로 바꾸고, inner product 에서 dot product 를 썼다.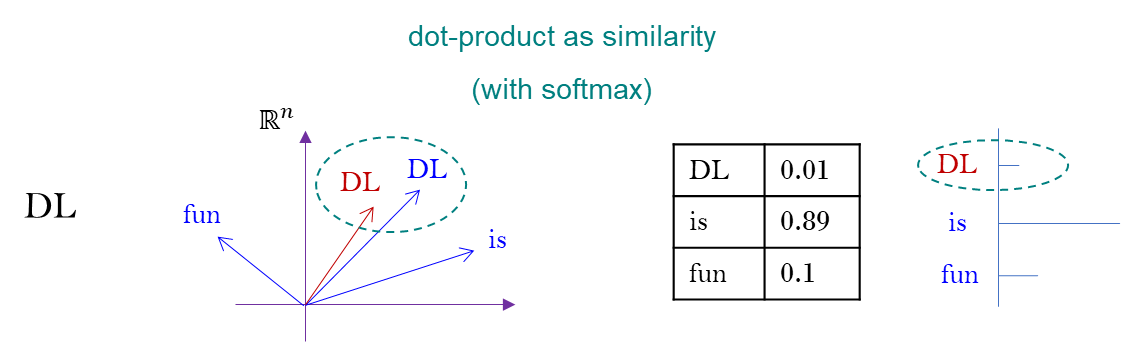

이것을 가지고 이 예시에서 보면 DL vector 들 끼리 similarity 가 있다, 이런 이야기를 하고 싶었던 것이다. 그러면 DL is fun 이 집합에 inner product 를 부여할 수 있는 그런 structure 를 주고 있다. 그래야지만 transformer 를 할 수 있다.
그런데, 집합에 inner product 를 주는 방법은 2가지 밖에 없다.
- 하나는 집합 자체가 vector space 이던가,
- 또 하나는 $\mathbb{R}^n$ 의 부분집합 자체가 manifold structure 자체를 들고 있다.
이렇게 이야기 할 수 밖에 없다. (그러나 이들의 모임은 $\mathbb{R}^n$ 의 모임이 아니다.) 그리고 dot product 를 들고 와서 전체 inner product 를 하고 있는 것이다.
DL is fun 의 모임을 manifold 로 보고 있는데, 어떤 inner product 를 사용하고 있냐면, 전체 집합에 해당하는 euclidean space 의 dot-product 를 그대로 가져다가 쓰고 있다. 그래야지만 위와 같은 설명이 타당하게 된다.
단어들이나 문장들이 euclidean space 의 vector 와 문장들의 matrix 로써 잘 표현하는 대전제에서 하고 있다. 공간 자체가 euclidean space 에 잘 들어간 다는 전제에서 하고 있다. 단어들의 모임을 어디에 집어 넣고, 이것이 $\mathbb{R}^n$ 의 부분 집합으로써 들어갔기 때문에, 그래야지만 위와 같은 설명이 가능하다.

결론은 DL is fun 이들을 $\mathbb{R}^n$ 에 집어 넣고, $\mathbb{R}^n$ 에 dot-product 에 쓰고 있는데 그러면 문제가 있다.

Riemann Geometry

이와 관련한 Riemann Geometry 에서는 두 가지 중요한 정리가 있다.

Whitney embedding theorem

임의의 $n$ 차원 미분 다양체는 위상 동형 으로서 $\mathbb{R}^{2n}$ 의 부분 공간으로 간주할 수 있다.

( 단, Riemann metric 은 보존하지 않는다. )
- 미분 다양체를 쓰게 되면, Riemann metric 에 강조점이 없다.
- manifold 만 존재하고, metric 은 무엇이 되어도 상관이 없다.
- Riemann metric 없는 shape 을 생각하지 않는 찰흙 덩어리로써 차원이 2배 높은 $(\mathbb{R}^{2n})$ 의 부분 공간 으로는 언제나 간주할 수 있다.
임의의 manifold 가 있고, Riemann metric 을 생각하지 않으므로 shape 을 보지 않는다. 임의의 Riemann manifold 는 차원이 2배 높은 euclidean space 에 들어있는 것 처럼 생각해도 된다.
J.Nash isometric embedding theorem

임의의 $n$ 차원 리만 다양체 $\left( M, g \right)$ 를 $f : M \longrightarrow \mathbb{R}^m, \quad m \geq n + 1$ 에 대해 미분 동형 으로서 $\mathbb{R}^n$ 의 부분 공간으로 가정하면, Riemann metric $g$ 까지 보존하는 embedding.

$\tilde{f} : (M, g) \longrightarrow (\mathbb{R}^{n}, g_{\mathbb{R}^n}), \quad \left(i.e.\;, \tilde{f}^{*}g_{\mathbb{R}^{n}}=g \right)$
- 그러나, 위의 해석을 하기 위해서는 shape 도 필요하다.
- Riemann metric 을 생각하겠다. shape 을 생각 해야만 Riemann manifold 가 된다.
- Manifold 를 $\mathbb{R}^n$ 에 집어 넣었다고 가정을 하자.
- 미분 동형으로 넣겠다는 것은 미분 구조를 다 보존하는 관점에서 넣는 것. 찰흙 덩어리가 아니라 좀더 쌔게 넣는 것 이지만, 아직 $g$ 를 보존하는 것은 아니다.
- 그렇게 된다고 하면, 언제나 metric 까지 보존할 수 있다.

Whitney embedding

i. 찰흙 덩어리로써 euclidean space 에 집어 넣을 수 있다.
ii. 미분 다양체, 위상 동형

J.Nash embedding

i. shape 까지 보장하는 sense 에서 euclidean space 에 집어 넣을 수 있다.
ii. 리만 다양체, 미분 동형 (미분 구조 보존), Riemann metric 까지 보존하는 embedding 이 Nash 에 의해서 존재, 중요하다.
iii. 결과적으로 shape 보장, Riemann metric 보존 하여 euclidean space 에 집어 넣을 수 있다.

Result

여기서 생각을 잘해야 하는 것은 $\mathbb{R}^n$ 에 dot-product 를 정확하게 J.Nash embedding 로 데려올 때, 우리가 들고 있는 metric $\left( M, g \right)$ 이 보장 되는 것을 확인하고 데려오는 것이다.

$\mathbb{H}^2$ 를 $\mathbb{R}^2$ 에 넣는 것으 생각하면 안된다. 반면에 $S^2$ 를 $\mathbb{R}^3$ 에 넣는 것이 이 상황이다. $\mathbb{R}^3$ 의 dot-product 를 $S^2$ 에 주면, 그것이 정확하게 $S^2$ 의 shape 을 결정하는 metric 이 나오게 된다.

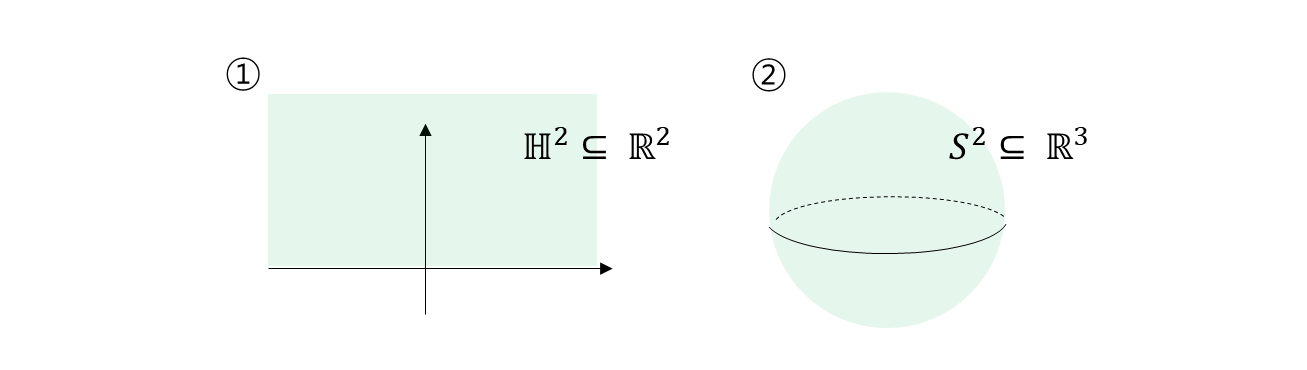
이것이 Riemann manifold 라면 J.Nash embedding 에 부합하는 예시가 된다. dimension 은 다를 수 있다. 어떠한 Riemann manifold 라면 dot-product 를 가지고 다시 봤을 때, 그 shape 이 정확하게 나오는 그러한 embedding 을 찾을 수 있다.

Transformer 의 대전제는 단어 및 문장들을 euclidean space $\mathbb{R}^n$ 의 vector 및 matrix 로 잘 표현 되어야 한다. 그러면 이것은 더 큰 공간으로 보고 있다. 거기서 shape 까지 보존하고 있어야 한다. 이와 같은 방법이 reasonable 하려면, 이와 같이 각도를 재는 행위 자체가 기존의 작은 manifold level 에서 shape 을 생각하는 것과 같다라는 전제이어야 말이 된다.

다시 말해서 $\mathbb{H}^2$ 와 $\mathbb{R}^2$ 상황을 생각해보자. $\mathbb{H}^2$ 에 $\mathbb{R}^2$ dot-product 가지고 $\mathbb{H}^2$ 의 geometric 을 재면, 완전 다른 이야기가 된다. 그것은 metric 이 맞지 않으므로, 아무 상관없는 행동이 된다. 적어도 $\mathbb{H}^2$ 에서는 내적이 $\rm{Poincar\acute{e} \; metric}$ 이어야 한다.