02. 완전탐색 문제 [BOJ 15686번]

1. 관련 문제 🎯

문제 : 백준 15686 치킨 배달 🍗
난이도 : 골드 5

2. 문제 속 정보 🧩

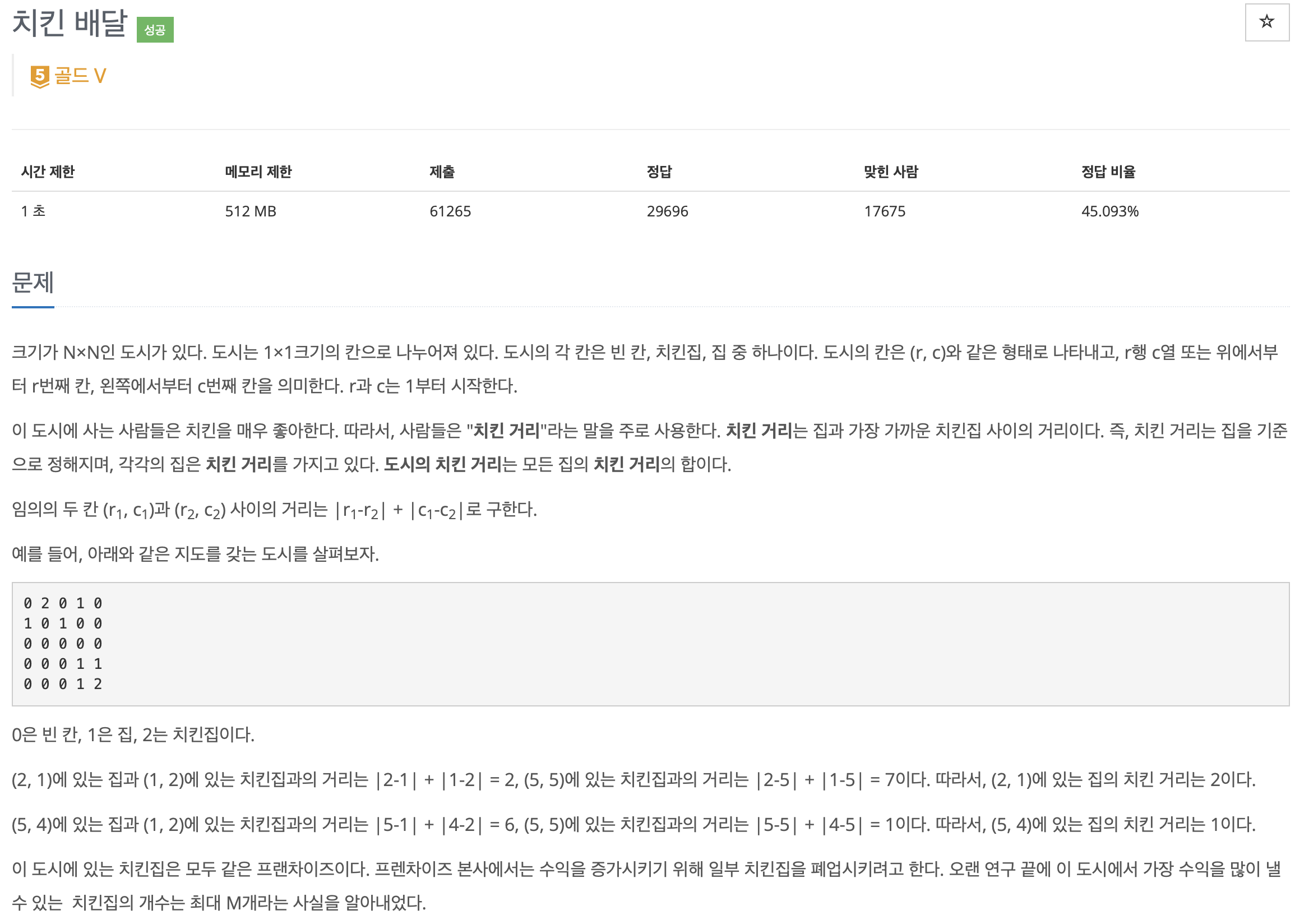
1) 도시 정보 : 0 = 빈칸, 1 = 집, 2 = 치킨 집
1) 치킨 거리 : 집과 가장 가까운 치킨집 사이의 거리
즉, 치킨 거리는 집을 기준으로 정해지며, 각각의 집은 치킨 거리를 가지고 있다.
2) 도시의 치킨 거리 : 모든 집의 치킨 거리의 합
4) (r1, c1)과 (r2, c2) 사이의 거리 = |r1-r2| + |c1-c2|

3. 문제 풀이 🖌️

1. 집의 위치와 치킨의 위치를 각각 저장한다.
2. 치킨집 중에서 M개의 치킨집을 선택한다. (조합)
3. 각각 집마다 선택된 M개의 치킨집 중에서 가장 가까운 치킨 집까지의 거리(치킨 거리)를 구한다.
4. 선택한 M개의 치킨 집 조합마다 모든 집의 치킨거리의 합(도시의 치킨 거리)를 구하고 그 중에서 가장 작은 도시의 치킨 거리를 구한다.

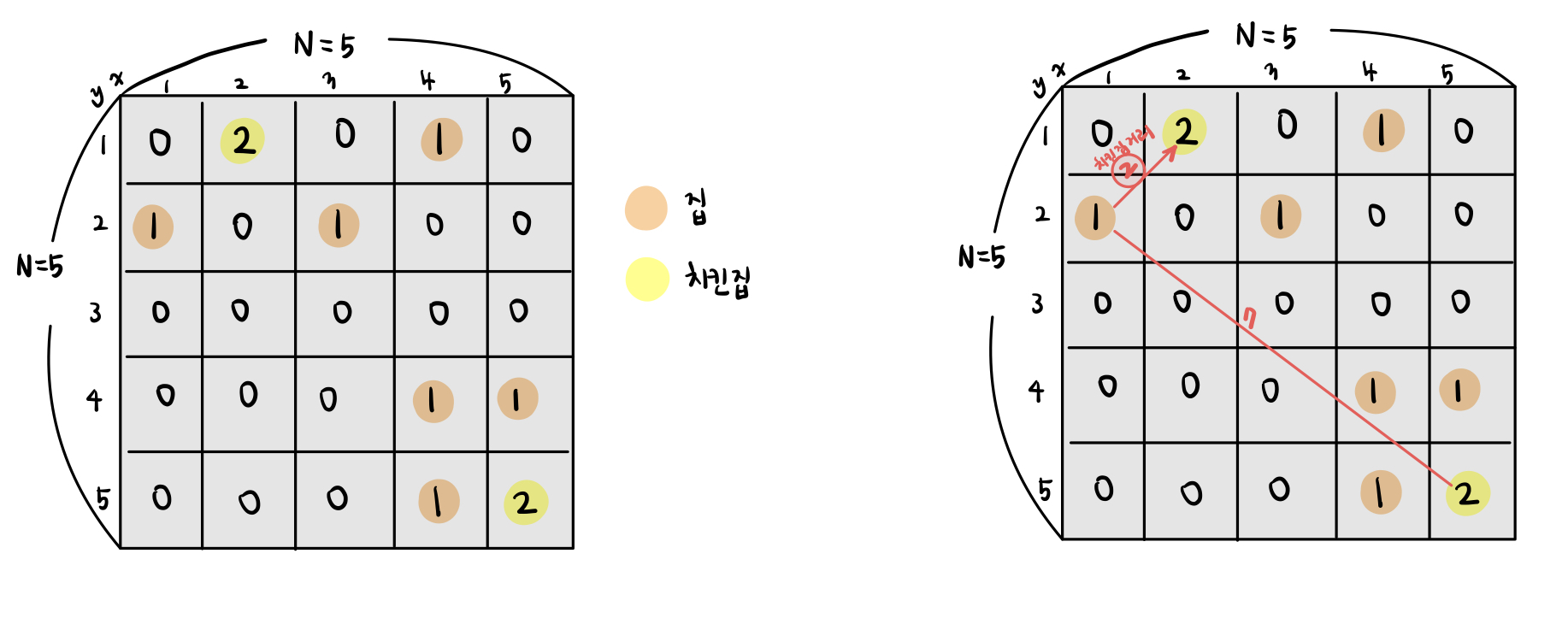
• 이때, 중요한 점은 집을 기준으로 최소 거리인 치킨 집을 선택해야 한다는 것이다.
• 아래의 그림을 보면, [왼쪽 그림]은 집을 기준으로 최소 거리를 구한 것이다.
  이때, 치킨 집은 (2,1)인 위치만 선택되고, (5,5) 위치인 치킨 집은 선택되지 않는다. 하지만, 최대 M개의 치킨집을 사용하면 되므로 M개 이하의 치킨 집이 선택되도 된다.
• [오른쪽 그림]은 치킨 집을 기준으로 최소 거리인 집을 선택한다.
  이때, (4,1)의 집과 (3,3)의 집은 선택되지만, (1,3)의 집은 선택되지 않는다.
  따라서, 집은 모두 선택되어야 하므로 집을 기준으로 최소 거리인 치킨 집을 구하면 된다.

4-1. 코드 (시간 초과) ⏳

• algorithm 라이브러리에서 구현된 next_permutation을 사용하여 조합을 구현하였다. 그러나, next_permutation을 사용하여 구현한 조합은 큰 수에서 dfs로 구현한 조합보다 시간이 오래 걸려서 dfs로 직접 구현하는 것이 좋다.

#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
using namespace std;

int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(NULL); cout.tie(NULL);

    int N =0, M=0;  //도시의 크기, 치킨집의 최대 개수
    int city=0;    //도시의 정보 (0 : 빈칸, 1 : 집, 2 : 치킨집)
    vector<pair<int,int>> home; //집의 좌표
    vector<pair<int,int>> chicken;  //치킨 집의 좌표
    
	//1. 집의 위치와 치킨의 위치를 각각 저장한다.
    cin>>N>>M;
    for(int i=1; i<=N; i++){
        for(int j=1; j<=N; j++){
            cin>>city;
            if(city == 1) home.push_back({i,j});
            else if(city == 2) chicken.push_back({i,j});
        }
    }

    //조합 구하기 - 보조 수열(전체 길이가 n개 , 1의 개수가 r개, 나머지가 0)
    vector<int> visit;
    for(int i=0; i<chicken.size()-M; i++){
        visit.push_back(0);
    }
    for(int i=0; i<M; i++){
        visit.push_back(1);
    }

    int min_homes_sum = 0x3f3f3f;
    do{ 
        int homes_sum = 0;
        for(int i=0; i<home.size(); i++){
            int min_home_sum = 0x3f3f3f;
            for(int j=0; j<chicken.size(); j++){
                if (visit[j] != 0) {
                    int sum = abs(chicken[j].first-home[i].first) + abs(chicken[j].second-home[i].second);
                    if(sum < min_home_sum) min_home_sum = sum;    
                    //3. 각각 집마다 선택된 M개의 치킨집 중에서 가장 가까운 치킨 집까지의 거리(치킨 거리)를 구한다.
                }
            }
            homes_sum = homes_sum + min_home_sum;
            //4-1. 선택한 M개의 치킨 집 조합마다 모든 집의 치킨거리의 합(도시의 치킨 거리)를 구한다.
        }
        if(min_homes_sum > homes_sum) min_homes_sum = homes_sum;	
        // 4-2. 그 중에서 가장 작은 도시의 치킨 거리를 구한다.
    }while(next_permutation(chicken.begin(), chicken.end()));	
    //2. 치킨집 중에서 M개의 치킨집을 선택한다. (조합)

    cout<<min_homes_sum<<"\n";
}

4-2. DFS로 조합 구현하기 🎄

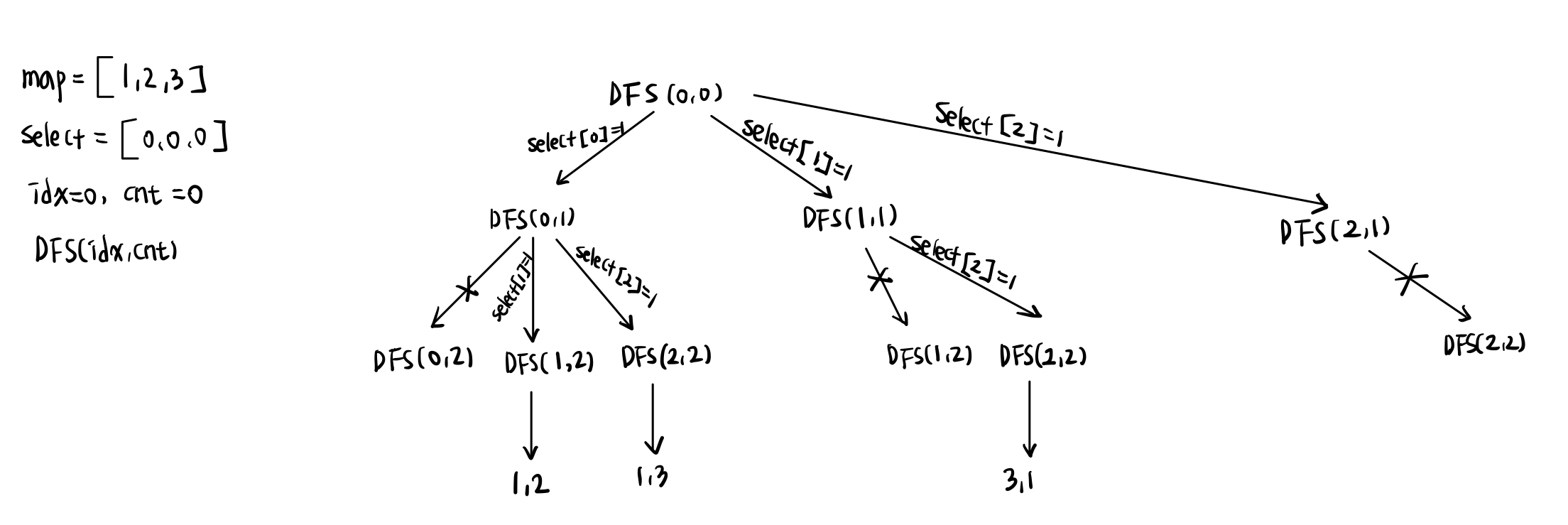
• 위의 그림을 아래의 코드를 사용하여 표현해보면, 다음과 같이 된다.
• 이때, idx의 역할은 화살표가 오른쪽 방향으로만 향하게 하는 것이다.
  조합에서는 1->2->3과 3->1->2가 동일하기 때문이다.
• select 배열은 '중복 방지' 역할을 한다.
  (따라서, 중복 조합의 경우 중복을 허용하므로 select 배열을 사용하지 않는다.)
  select 배열을 사용하여 이미 뽑은 공인지를 확인한다.

#include <iostream>
#include <vector>
using namespace std;

vector<int> vec;
vector<int> map = {1,2,3};
bool check[3];

void DFS(int idx, int cnt){
    cout<<"("<<idx<<","<<cnt<<")\n";
    if(cnt == 2){
        for(auto iter : vec){
            cout<<iter<<" ";
        }
        cout<<"\n";
        return;
    }

    for(int i=idx; i<map.size(); i++){
        if(check[i]==true) continue;
        check[i]=true;
        vec.push_back(map[i]);
        DFS(i,cnt+1);
        check[i]=false;
        vec.pop_back();
    }
}

int main(){
    DFS(0,0);
}

참고자료 : 순열과 조합 DFS로 구현 📒
https://charles098.tistory.com/9
https://paris-in-the-rain.tistory.com/35

4-3. 성공한 코드 🔑

• 앞에서 시간 초과한 코드에서 조합 구현을 제외한 나머지 부분은 동일하다!

#include <iostream>
#include <vector>
#include <cmath>
using namespace std;

int N =0, M=0;  //도시의 크기, 치킨집의 최대 개수
vector<pair<int,int>> vec;	//선택된 M개의 치킨 집
vector<pair<int,int>> home; //집의 좌표
vector<pair<int,int>> chicken;  //치킨 집 번호, 치킨 집의 좌표
int min_homes_sum = 0x3f3f3f;
bool check[13];

void DFS(int idx, int cnt){
    if(cnt == M){	//M은 구하고 싶은 개수
        int homes_sum = 0;
        for(int i=0; i<home.size(); i++){
            int min_home_sum = 0x3f3f3f;
            for(int j=0; j<vec.size(); j++){
                int sum = abs(vec[j].first-home[i].first) + abs(vec[j].second-home[i].second);
                if(sum < min_home_sum) min_home_sum = sum;
                //3. 각각 집마다 선택된 M개의 치킨집 중에서 가장 가까운 치킨 집까지의 거리(치킨 거리)를 구한다.
            }
            homes_sum = homes_sum + min_home_sum;
           //4-1. 선택한 M개의 치킨 집 조합마다 모든 집의 치킨거리의 합(도시의 치킨 거리)를 구한다.
        }
        if(min_homes_sum > homes_sum) min_homes_sum = homes_sum;
        // 4-2. 그 중에서 가장 작은 도시의 치킨 거리를 구한다.
        return;
    }

    for(int i=idx; i<chicken.size(); i++){
        if(check[i]==true) continue;
        check[i]=true;
        vec.push_back(chicken[i]);
        DFS(i,cnt+1);
        check[i]=false;
        vec.pop_back();
    }
}

int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(NULL); cout.tie(NULL);

    int city=0;    //도시의 정보 (0 : 빈칸, 1 : 집, 2 : 치킨집)
	
    //1. 집의 위치와 치킨의 위치를 각각 저장한다.
    cin>>N>>M;
    for(int i=1; i<=N; i++){
        for(int j=1; j<=N; j++){
            cin>>city;
            if(city == 1) home.push_back({i,j});
            else if(city == 2) chicken.push_back({i,j});
        }
    }

    DFS(0,0);	//idx = 0, cnt = 0
    cout<<min_homes_sum<<"\n";
}

5. 결과 🏆