08. DP 문제 [BOJ 2293번]

1. 관련 문제 🎯

문제 : 백준 2293 동전 1 👛
난이도 : 골드 5

2. 문제 소개 🧩

1️⃣ n가지 서로 다른 종류의 동전이 있다.
2️⃣ 이 동전을 사용하여 그 가치의 합이 k원이 되도록 하는 경우의 수를 구해야 한다.

예시1) 1원, 2원, 5원의 동전으로 10원이 되도록 하는 경우의 수를 구하여라.

3. 문제 풀이 🖌️

3-1. 점화식 구하기

점화식을 구하다가, 계속 에러가 나와서 다른 사람들의 풀이를 참고했다 😿
참고 자료 : https://bitwise.tistory.com/504

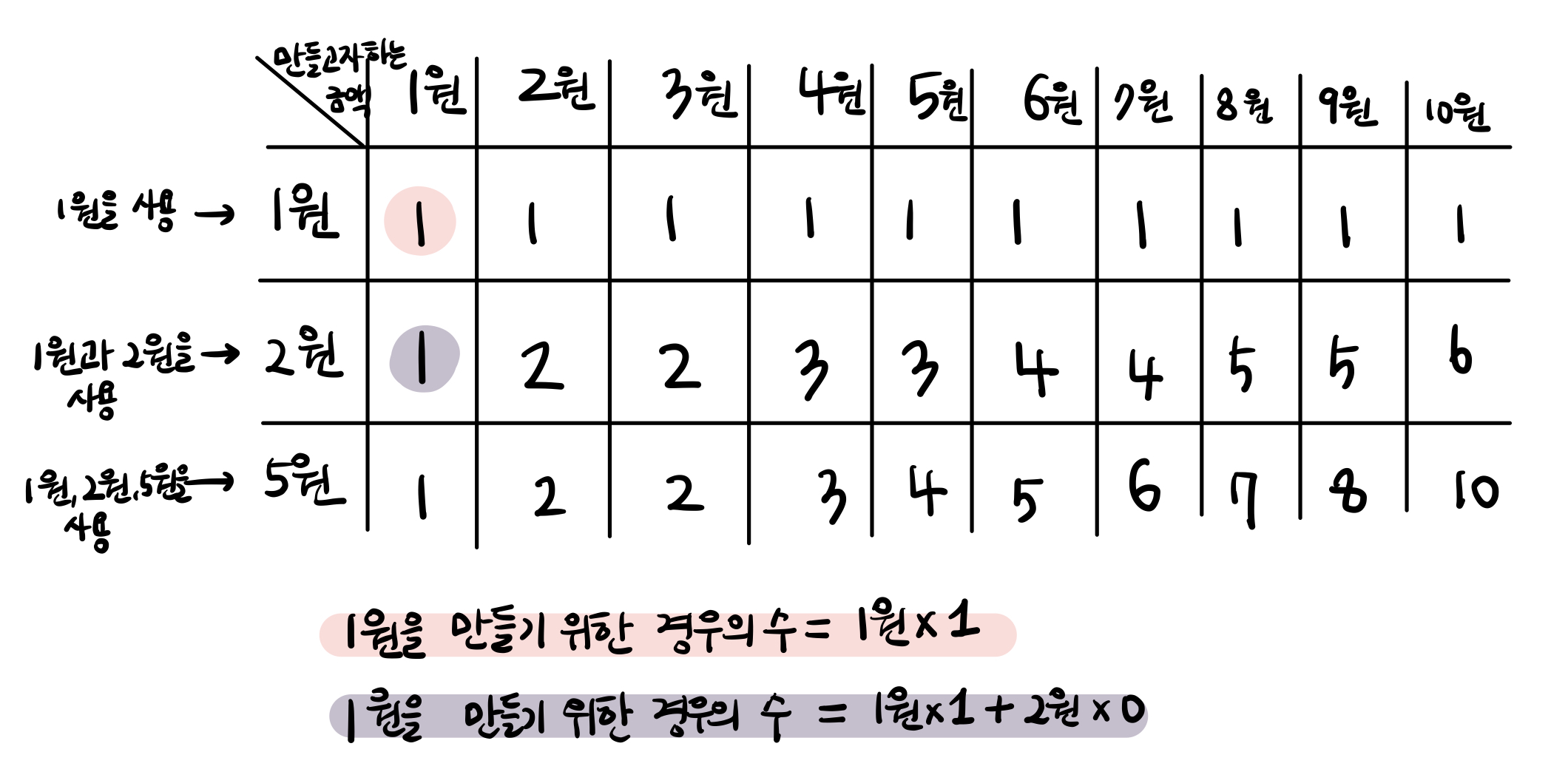
• 먼저, 1원을 만들기 위해서는 1원만을 사용하여 1원 x 1인 1가지의 경우의 수가 있다.
  그리고 1원과 2원을 사용하여 1원 x 1 + 2원 x 0인 1가지의 경우의 수가 있다.
  마지막으로 1원과 2원, 5원을 사용하여 1원 x 1+ 2원 x 0 + 5원 x 0인 1가지의 경우의 수가 있다.
  즉, 1원을 만들기 위해서 1원, 2원, 5원을 사용하면 총 1가지의 경우의 수가 있다.
  따라서 1원의 열을 보았을 때 1원, 2원, 3원 행은 앞의 행을 누적한 값임을 알 수 있다.
• 두 번째로, 2원을 만들기 위해서는 1원 x 2와 2원 x 2인 2가지의 경우가 나온다.

3-2. 자세하게 살펴보기

• 먼저, 1원만을 사용한 예시를 살펴보면 모두 1가지 경우의 수가 나온다는 것을 알 수 있다.
  
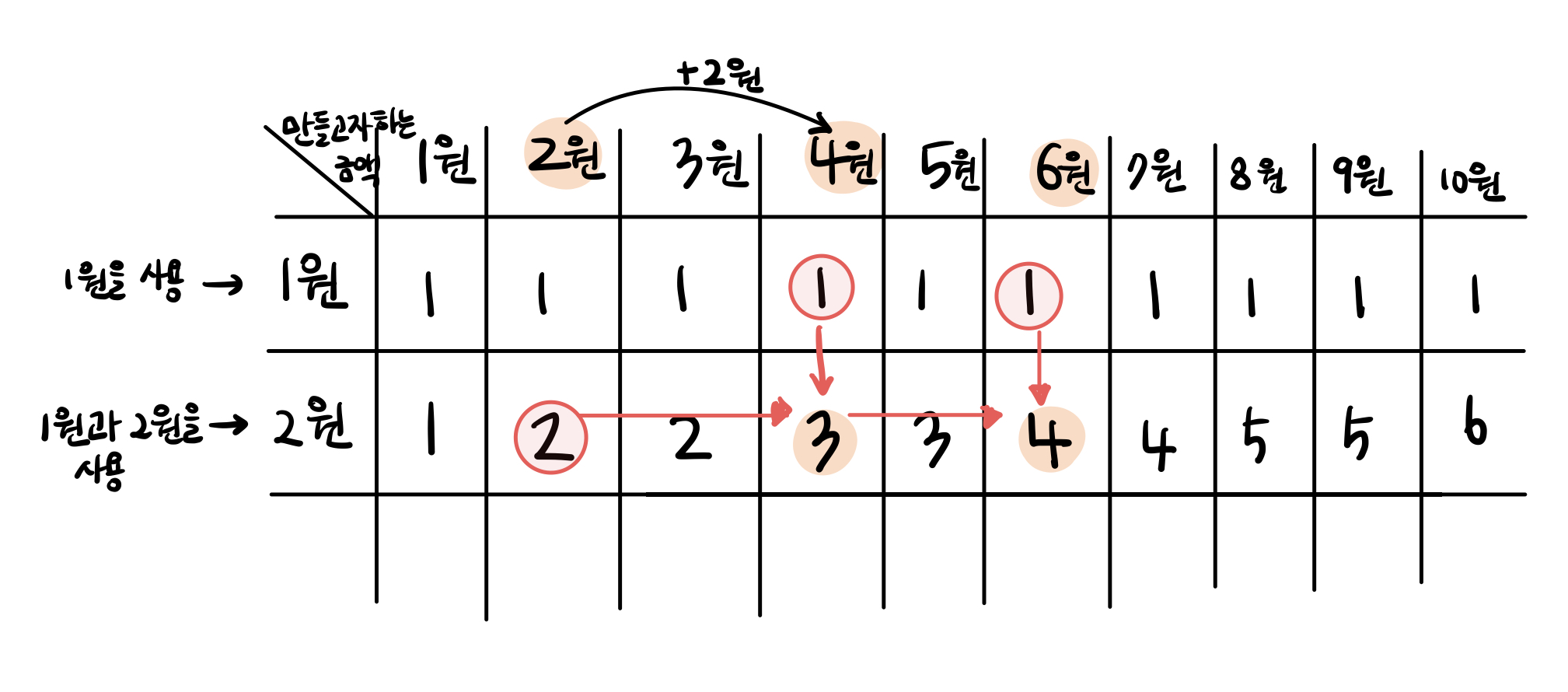
• 두번째로는 1원과 2원을 사용한 예시를 살펴보면, 4원을 만들기 위해서는 4원 - 2원 = 2원 이므로 즉 4원을 만들기 위한 공식은 (1원을 사용하여 4원을 만들기 위한 경우의 수) + (1원과 2원을 사용하여 2원을 만들기 위한 경우의 수)이다.
• 이러한 공식을 계속 사용하여 1원과 2원을 사용하여 2번째 행을 다 완성할 수 있다.
  
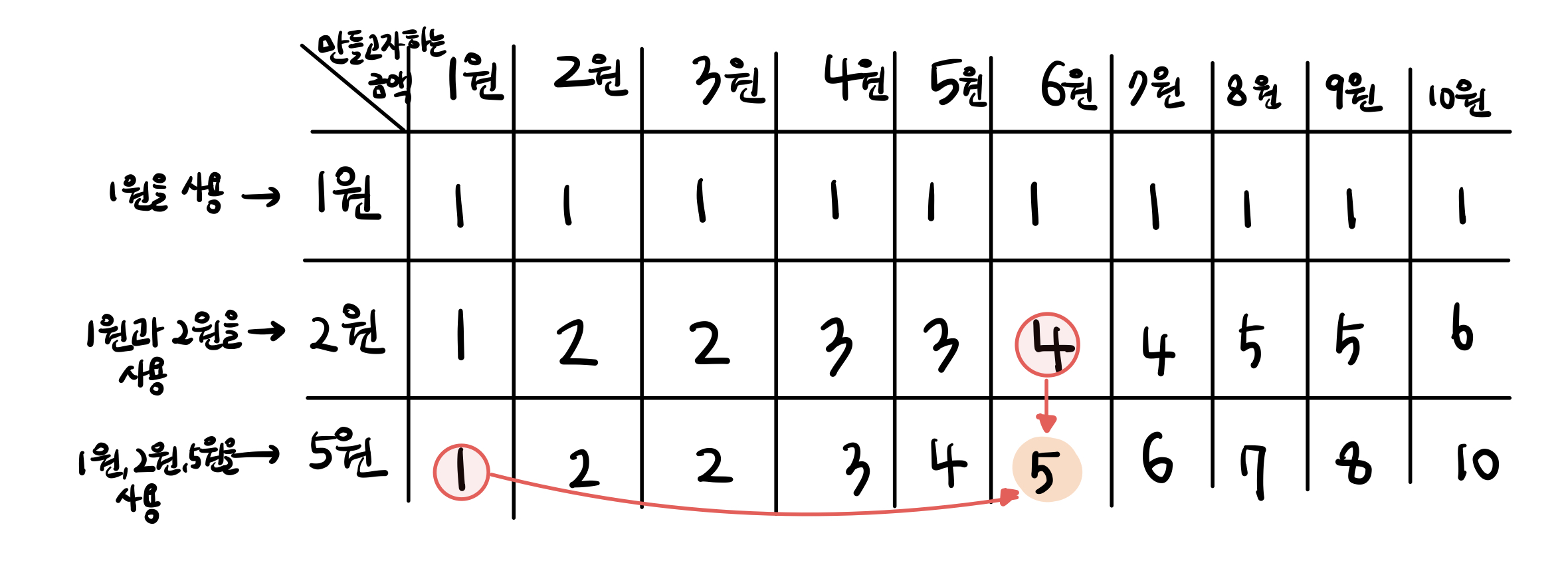
• 마지막으로 1원과 2원, 5원을 사용한 예시를 살펴보자!
  6원(6원 = 1원 + 5원)을 만들기 위해서는 (1원과 2원을 사용하여 6원을 만들기 위한 경우의 수) + (1원과 2원, 5원을 사용하여 1원을 만들기 위한 경우의 수) = 1+4=5이다.
• 메모리 제한이 4 MB이므로 하나의 배열만을 사용하여 구한다!!
• 즉, dp[6원] = dp[6원] + dp[6원-5원] = dp[6원] + dp[1원] = 1+4 = 5이다.
  

점화식 : dp[j]는 하나의 행을 의미한다. coin[i]는 동전의 종류를 의미한다.
dp[j] = dp[j - coin[i]] + dp[j]

4. 전체 코드 🔑

#include <iostream>
using namespace std;

int main() {
    std::ios::sync_with_stdio(false); 
    cin.tie(NULL); cout.tie(NULL);

    int n, k; 
    cin >> n >> k;
    int coin[100];
    int dp[10001] ={0,};

    for (int i = 0; i < n; i++) {
        cin >> coin[i];	//동전의 종류를 입력받는다.
    }

    dp[0] = 1;
    for (int i = 0; i < n; i++) {
        for (int j = coin[i]; j <= k; j++) {	
        //coin[i]전까지는 이전 값과 동일하므로 coin[i]부터 시작한다.
            dp[j] += dp[j - coin[i]];	//점화식
        }
    }

    cout << dp[k] << "\n";
    return 0;
}

5. 결과 🏆