10. 최단 경로 문제 [BOJ 13549번]

1. 관련 문제 🎯

문제 : 백준 13549 숨바꼭질3 💁‍♀️
난이도 : 골드 5

2. 문제 소개 🧩

1️⃣ 수빈이는 현재 점 N(0 ≤ N ≤ 100,000)에 있고, 동생은 점 K(0 ≤ K ≤ 100,000)에 있다.

• 수빈이는 동생이 있는 곳까지 최단 시간 안에 이동해야 한다. = 최단 거리 문제

2️⃣ 수빈이는 걷거나 순간이동을 할 수 있다.

• 만약, 수빈이의 위치가 X일 때 걷는다면 1초 후에 X-1 또는 X+1로 이동하게 된다.
• 순간이동을 하는 경우에는 0초 후에 2*X의 위치로 이동하게 된다.

  즉, 최단 거리 문제 중에서 그래프 간선에 가중치가 0또는 1이 있는 문제라고 할 수 있다!!
  그러나, BFS는 최단 거리 문제 중 그래프 간선에 가중치가 없는 문제는 해결할 수 있다.
  따라서 다익스트라 알고리즘를 사용하여 문제를 해결해야 한다!!

3. 문제 풀이 🖌️

참고한 풀이 : https://jdselectron.tistory.com/58

3-1. 수빈이의 위치와 동생의 위치를 입력받는다.

• ☝️ 이때, 최단 거리를 구하기 전에 그래프를 생성해야 한다!
  왜냐하면 하나의 노드에서 인접한 노드들을 향해서 나아가기 위한 지도가 있어야 하기 때문이다!
• 그러나, 이번 문제의 경우 한 노드(X)에 대한 인접 노드들은 순간이동(2*X)하거나 걸어서(X-1, X+1) 가는 노드들로 정의할 수 있기 때문에 따로 그래프를 생성하지 않아도 된다.
• 수빈이의 위치를 시작 노드로, 동생의 위치를 종료 노드로 설정한다!!

int N = 0, K = 0;    //수빈이의 위치, 동생의 위치
cin >> N >> K;
... 생략 ...
que.push({0,N});    //걸린 시간, 위치
... 생략 ...
if(here == K)   break;

3-2. 우선순위 큐를 이용하여 다익스트라 알고리즘을 수행한다.

• while문을 돌면서 인접한 노드들(here*2, here+1, here-1) 중에서 방문하지 않은 노드들을 방문한다.
• 이때, 수빈이는 MAXSIZE(100001)~0까지만 움직일 수 있으므로 방문할 노드들의 값이 MAXSIZE가 넘거나 0 미만인 경우 방문하지 않는다.

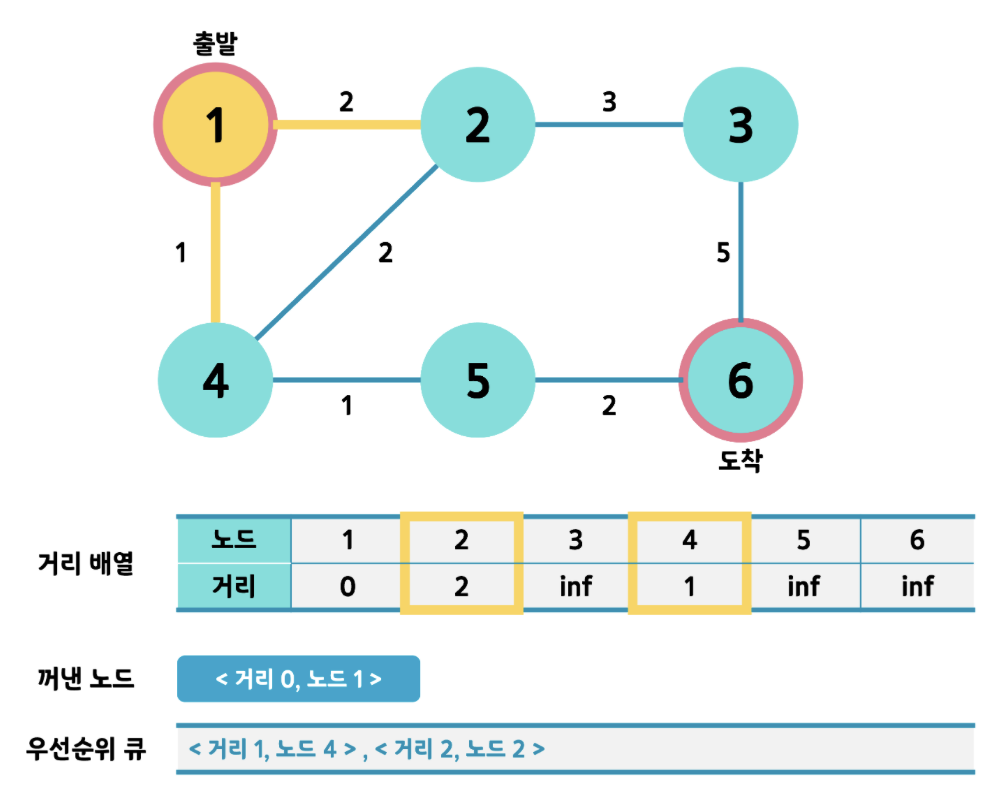
사진 출처 : https://velog.io/@717lumos/알고리즘-다익스트라Dijkstra-알고리즘#3-구현2-우선순위-큐
💁‍♀️ 더 자세한 내용은 위의 출처 블로그를 참고해주세요~!!

• 최단 경로를 구하기 위해서, 우선순위 큐를 사용한 다익스트라 알고리즘을 살펴보자!!
  그러면, 꺼낸 노드인 하나의 노드와 인접한 노드들을 거리와 노드 번호를 우선순위 큐에 넣는 것을 확인해볼 수 있다. 그리고 나서, 두 번째로 방문할 노드는 우선순위 큐에서 가장 맨 앞에 있는 노드이다!
• 이처럼, 이번 문제에서는 최단 거리가 아닌 최단 시간이므로 시간(time, time+1)과 노드 번호(here*2, here+1, here-1)를 우선순위 큐에 넣는다.

priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>>> que;
que.push({0,N});    //걸린 시간, 위치
check[N] = 1;

while(!que.empty()){
	int here = que.top().second;      //현재 위치
    int time = que.top().first;    //걸린 시간
    if(here == K)   break;
    que.pop();
    
    if(here*2 < MAXSIZE and check[here*2] == 0){
		check[here*2] = 1;
        que.push({time, here*2});   //순간이동
    }
    if(here+1 < MAXSIZE and check[here+1] == 0){
        check[here+1] = 1;
        que.push({time+1, here+1});   
    }
    if(here-1 >= 0 and check[here-1] == 0){
        check[here-1] = 1;
        que.push({time+1, here-1});   
    }
}

4. 전체 코드 🔑

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

int MAXSIZE = 100001;
int check[100001] = {0,};

int main() {
    std::ios::sync_with_stdio(false); 
    cin.tie(NULL); cout.tie(NULL);

    int N = 0, K = 0;    //수빈이의 위치, 동생의 위치
    cin >> N >> K;

    priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>>> que;
    que.push({0,N});    //걸린 시간, 위치
    check[N] = 1;

    while(!que.empty()){
        int here = que.top().second;      //현재 위치
        int time = que.top().first;    //걸린 시간
        if(here == K)   break;
        que.pop();

        if(here*2 < MAXSIZE and check[here*2] == 0){
            check[here*2] = 1;
            que.push({time, here*2});   //순간이동
        }
        if(here+1 < MAXSIZE and check[here+1] == 0){
            check[here+1] = 1;
            que.push({time+1, here+1});   
        }
        if(here-1 >= 0 and check[here-1] == 0){
            check[here-1] = 1;
            que.push({time+1, here-1});   
        }
    }

    cout<<que.top().first<<"\n";
}

5. 결과 🏆