[자료구조, 알고리즘] - 정렬, 탐색 알고리즘

---

...

정렬 알고리즘

---

1. 삽입정렬

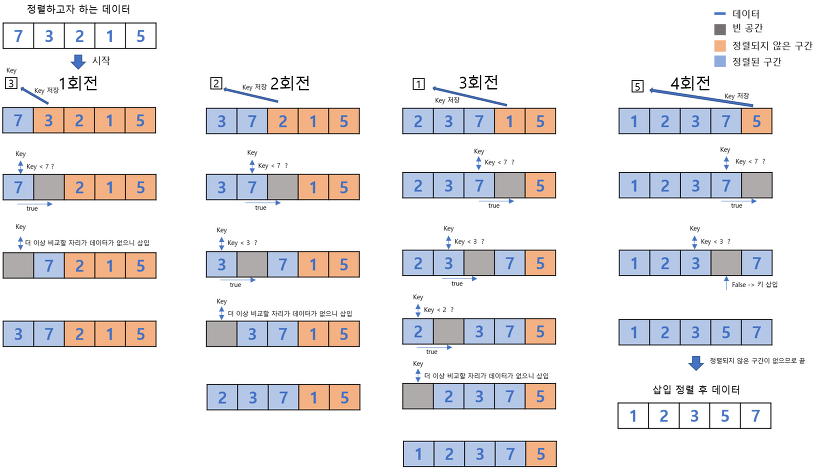
◾ 방법

2번째 원소(key)부터 시작하여 그 앞(왼쪽)의 원소들과 비교하여 삽입할 위치를 지정한 후, 원소를 뒤로 옮기고 지정된 자리에 자료를 삽입하여 정렬하는 알고리즘

◾ 장점

• 알고리즘이 단순하여 구현이 쉽다
• 정렬하고자 하는 배열 안에서 교환하는 방식으로 다른 메모리 공간을 필요로 하지 않는다 (제자리 정렬: in-place sorting)
• 안정 정렬(Stable Sort)이다

◾ 단점

• 평균과 최악의 시간복잡도를 보아 배열의 길이가 길어질수록 비효율적

2. 선택정렬

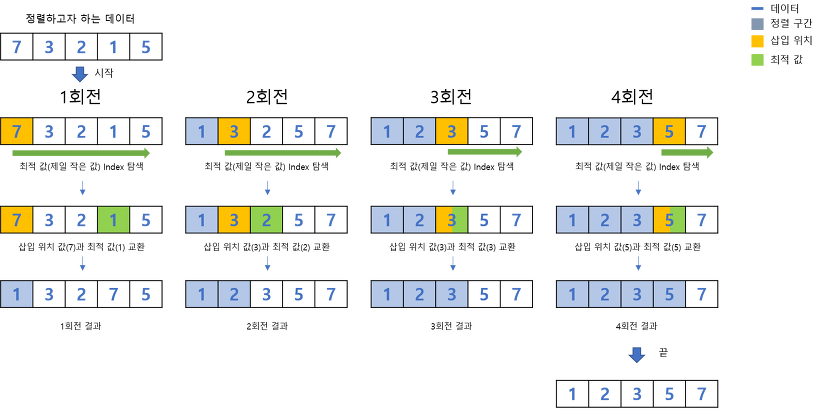
◾ 방법

해당 자리(key)로 옮길 원소를 뒤(오른쪽)에서부터 끝까지 탐색하면서 가장 작은 값을 찾아 교환하는 알고리즘

◾ 장점

• 알고리즘이 단순하여 구현이 쉽다
• 비교 횟수는 많지만 , 버블정렬에 비해 실제로 교환하는 횟수는 적기 때문에 많은 교환이 일어나야 하는 자료상태에서 비교적 효율적이다
• 정렬하고자 하는 배열 안에서 교환하는 방식으로 다른 메모리 공간을 필요로 하지 않는다(제자리 정렬:in-place sorting)

◾ 단점

• 매번 끝까지 탐색하면서 비교하므로 최선,평균,최악 O(n^2)로 비효율적이다
• 불안정 정렬(Unstable Sort) 이다

3. 버블정렬

◾ 방법

서로 인접한 두 원소를 비교하고 조건에 맞지 않는다면 자리를 교환하며 정렬하는 알고리즘

◾ 장점

• 알고리즘이 단순하여 구현이 쉽다
• 정렬하고자 하는 배열 안에서 교환하는 방식으로 다른 메모리 공간을 필요로 하지 않는다(제자리 정렬:in-place sorting)

◾ 단점

• 매번 끝까지 탐색하면서 비교하므로 최선,평균,최악 O(n^2)로 비효율적이다
• 교환연산이 많이 이뤄진다

4. 퀵 정렬

◾ 방법

전체를 분할기준(pivot)보다 작은 구간, 큰 구간으로 나누는 작업을 재귀적으로 수행하여 정렬하는 알고리즘

1. pivot을 정한다
2. (위치변수) left ++ , right– 를 거침
   ->분할을 하면서 left에다가는 pivot보다 큰 수의 위치, right에다가는 분할기준(pivot)보다 작은 수의 위치를 저장하고 교체한다
3. right이 left 와 같거나 작을 경우, right이 pivot보다 작을경우 값을 변경해준다
4. right 위치가 pivot이 되고 분할되어 반복

◾ 장점

• log N만큼 분할하고 분할마다 최대 n번 데이터 비교가 발생하므로 시간복잡도가 O(nlogn) 이므로 속도가 빠르다
• 정렬하고자 하는 배열 안에서 교환하는 방식으로 다른 메모리 공간을 필요로 하지 않는다. (제자리 정렬:in-place sorting)

◾ 단점

• 최악의 경우 : pivot이 매번 제일 크거나 작은 값을 선택될 때 , 이미 정렬된 데이터에 대해서 퀵 정렬을 수행할 때 (해결하기 위해 중간값을 pivot으로 선택한다)
• 불안정 정렬(Unstable Sort) 이다

5. 힙정렬

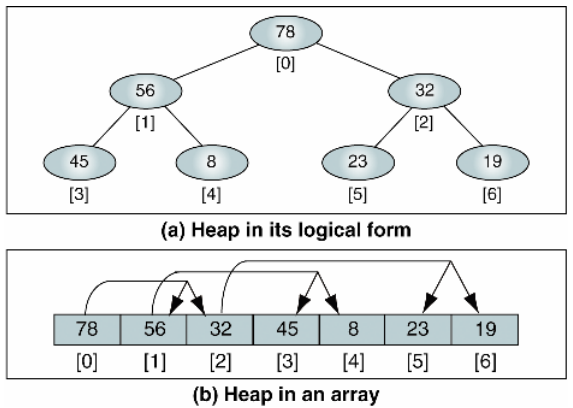
◾ 방법

완전 이진 트리 형태로 최대힙일 경우에는 내림차순으로, 최소힙일 경우에는 오름차순으로 정렬하는 알고리즘

• [최대힙일 경우 정렬방법]

1. root값을 빼준다
2. 힙의 마지막 노드를 root로 올린다
3. 자식노드와 비교하며 큰 값을 부모노드로 교환한다
4. 모든 노드가 빠질 때까지 반복한다

◾ 장점

• 전체 자료를 정렬하는 것이 아니라 가장 크거나 작은 값 몇개만 필요할 경우 유용하다

◾ 단점

• 불안정 정렬(Unstable Sort) 이다

6. 병합정렬

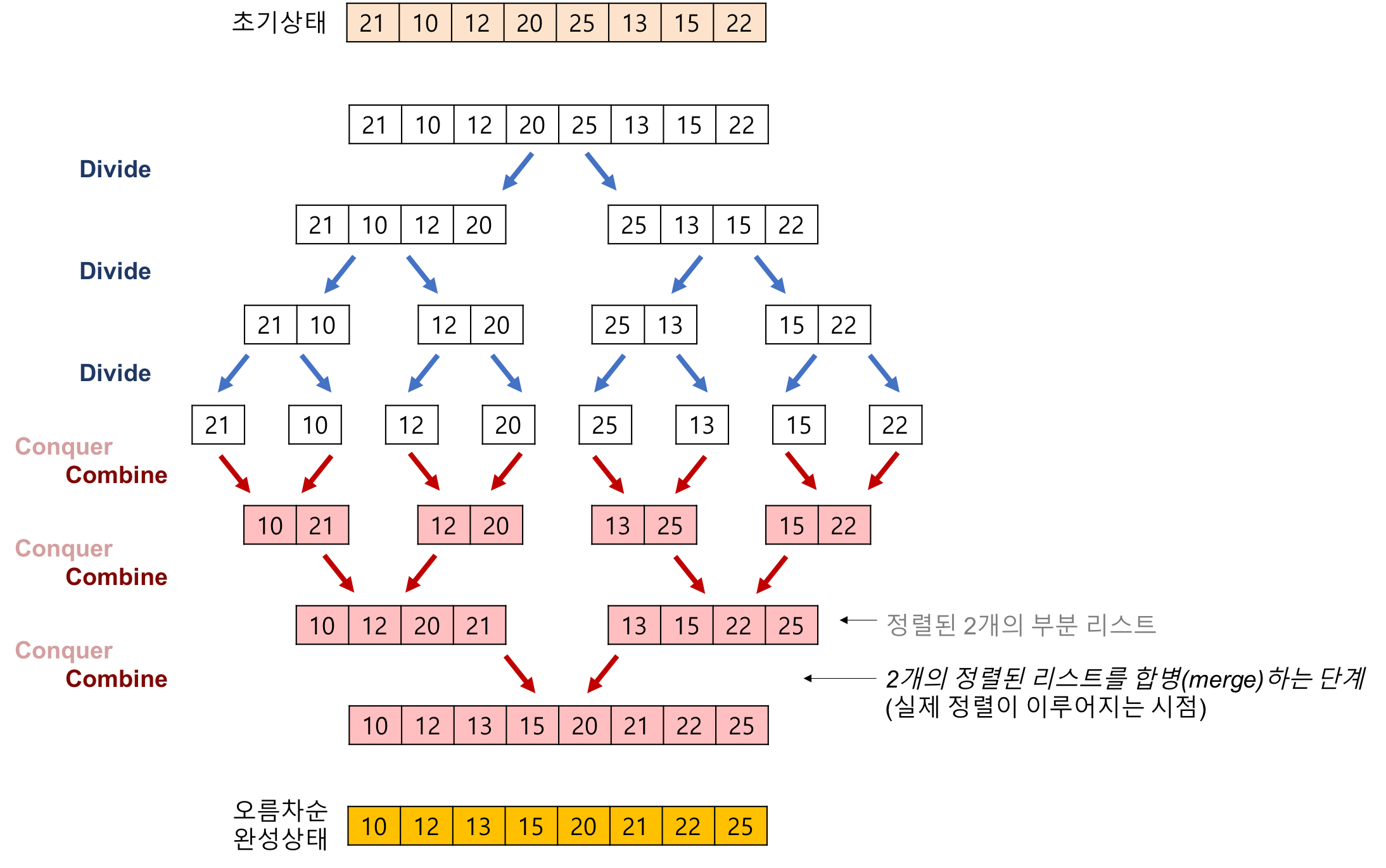
◾ 방법

원소를 하나일 때까지 절반씩 쪼갠 후 다시 합병시키면서 정렬하는 알고리즘

◾ 장점

• 안정 정렬로 입력 데이터가 무엇이든 간에 정렬되는 시간은 동일하다
• 데이터셋을 연결리스트로 구현하면 링크 인덱스만 변경하면 되므로 제자리 정렬로 구현할 수 있다

◾ 단점

• 거대한 데이터 셋일 경우 이동횟수가 많아지므로 매우 큰 시간적 낭비를 초래한다
• 제자리 정렬이 아니다
• 정렬 결과를 저장할 배열을 새로 만들고, 이를 기존에 배열에 복사하므로 거대한 데이터 셋에서 치명적이다

탐색 알고리즘

---

1. 선형탐색 (Linear Search)

맨 앞이나, 맨 뒤에서부터 순서대로 하나씩 찾아보는 알고리즘

◾ 방법

맨 앞이나, 맨 뒤에서부터 순서대로 하나씩 찾아보는 알고리즘

◾ 장점

• 단순하고 이해하기 쉽고 구현하기 쉽다

◾ 단점

• 데이터 수에 따라 시간이 늘어나므로 비효율적

🚦시간복잡도 : O(n)

• 최선인 경우 : 리스트의 첫 번째 원소가 정답인 경우 O(1)
• 최악의 경우 : 리스트의 맨 마지막 원소이거나 찾는 값이 없을 경우 O(n)

2. 이진탐색 (Binary Search)

탐색 대상인 데이터가 미리 정렬되어 있을 경우 사용할 수 있다. 가운데 요소보다 큰지 작은지 조건에 맞춰 탐색범위를 점점 좁힌다

◾ 방법

맨 앞이나, 맨 뒤에서부터 순서대로 하나씩 찾아보는 알고리즘

◾ 장점

• 선형탐색은 n이 증가함에 따라 시간복잡도가 선형적으로 증가하지만 , 이진탐색은 n이 증가해도 비교적 천천히 증가한다

🚦시간복잡도 : O(logn)

• 최선인 경우 : 리스트의 가운데 요소가 정답인 경우 O(1)
• 최악의 경우 : 리스트에 찾는 값이 없을 경우 O(logn)

3. 해시탐색 (Hash Search Search)

탐색 대상인 데이터가 미리 정렬되어 있을 경우 사용할 수 있다. 가운데 요소보다 큰지 작은지 조건에 맞춰 탐색범위를 점점 좁힌다

해시 함수를 거친 후 나오는 결과값으로 입력들을 분류하는 과정은 미리 준비해둔 상자(해시 테이블
=> 이렇게 미리 상자에 담아두면 나중에 해당 요소를 찾고자 할 때 빠르게 찾을 수 있다.**

◾ 방법

index와 그에 해당하는 값을 연결해 둠으로써 짧은 시간에 탐색할 수 있는 알고리즘

◾ 장점

• 데이터를 저장하거나, 탐색하고자 하는 위치를 즉시 참조할 수 있기 때문에 빠른 속도로 처리가 가능하다
• 효율적으로 배열을 사용할 수 있다

🚦시간복잡도 : O(logn)

• 최선인 경우 : 리스트의 가운데 요소가 정답인 경우 O(1)
• 최악의 경우 : 리스트에 찾는 값이 없을 경우 O(logn)

출처

이 블로그를 참고하여 작성하였습니다.