자료구조 정리2
...
- Hash Function, HashTable에 대해서 설명해주세요.
1. Hash & HashTable
해시 테이블(Hash Table)
◾ 정의
연관배열 구조를 이용해 key에 결과값(value)를 저장하는 자료구조.
◾ 연관배열 구조?
키 1개와 값 1개가 1:1로 연관되어 있는 자료구조
=> 이로인해 키(key)를 이용하여 값(value)을 도출할 수 있다.
📣 정리하면.. Key값을 해시함수를 통하여 인덱스로 변환 후에, 그 인덱스에 집어 넣는다.
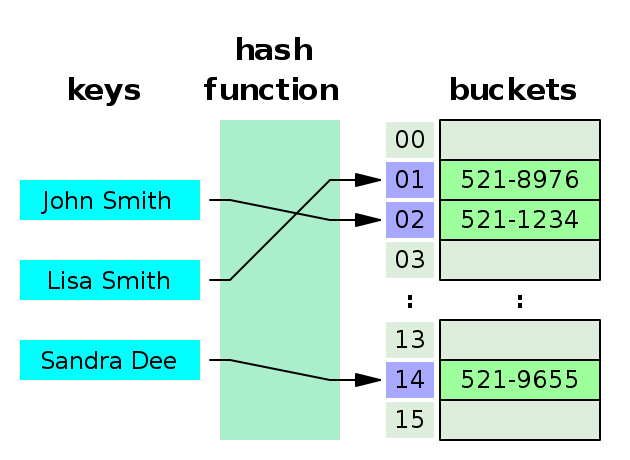
<구조>
- 키(key): 해시 함수의 input으로 해시 함수로 값을 바꾸어 저장해야 한다.(공간 효율성을 위해)
- 값(Value) : 저장소(bucket, slot)에 최종적으로 저장되는 값으로 키와 매칭되어 저장, 삭제, 검색, 접근이 가능해야 한다.
- 해시(Hash) : 해시 함수의 결과물이며, 저장소(bucket, slot)에서 값(value)과 매칭되어 저장된다.
- 해시함수 :
키를 해시(hash)로 바꿔주는 역할
-> 키(key)를 일정한 길이를 가지는 해시(hash)로 변경하여 저장소를 효율적으로 운영할 수 있도록 도와준다.
-> 해시 충돌을 일으키는 확률을 최대한 줄이는 함수를 만드는 것이 중요
해시 충돌
Hash Table은 내부적으로 배열을 사용해 빠른 탐색 속도를 가진다 => O(1)
💬 '해시충돌'의 의미
만약 위처럼 key값을 해시함수를 통해 변환하는데 다른 key 값을 넣어서 해시함수가 통과되었을 때 다른 것과 같은 인덱스가 나오는 것을 충돌이라고 한다.
<충돌 해소법>
크게 두 가지 방식으로 나뉜다.
-
Open Address 방식 (개방 주소법) : 충돌 발생 시, 다른 인덱스를 찾는다.
- 선형 탐색(Linear Probing): 순차적으로 탐색하여 다음 인덱스를 찾는다.
- 제곱 탐색(Quadratic Probing): 충돌이 일어난 해시의 제곱을 한 해시에 데이터를 저장한다.
- 이중 해시(Double Hashing): : 충돌 발생시 새로운 해시함수를 활용하여 주소를 찾는다.
-
Separate Chaining 방식 (분리 연결법) : 다른 인덱스를 찾는 대신, 그 인덱스에다가 연결하는 방법.
¹연결 리스트를 이용하여 연결하는 방법과, ² Tree(RBT)를 이용하여 연결하는 방법이 있다.
=> 두 방식 모두 Worst Case가 O(M)이다.
=> 그렇기에 만일, 데이터의 크기가 크다면 Separate Chaining, 아니라면 Open Address 방식이 더 낫다. 🤔
- Tree, Binary Tree, BST, AVL Tree에 대해서 설명해주세요.
Tree
◾ 정의
Stack, Queue와는 다르게 비선형 자료구조로, 계층적 구조를 표현하는 자료구조이다.

◽ 구성요소
- Node (노드) : 트리를 구성하고 있는 원소 그 자체를 말한다.
- Edge (간선) : 노드와 노드사이를 연결하고 있는 선을 말한다.
- Root(Node) : 트리에서 최상위 노드를 말한다.
- Terminal(Node) : 트리에서 최하위 노드를 말한다. Leaf Node라고도 한다.
- Internal(Node) : 트리에서 최하위 노드를 제외한 모든 노드를 말한다.
Binary Tree (이진트리)
◾ 정의
Binary Tree 는 모든 노드들이 둘 이하(0,1,2 개)의 자식을 가진 트리이다.
- 모든 Level이 가득 찬 이진 트리인 Full Binary Tree(포화 이진 트리) 와 위에서 아래로, 왼쪽에서 오른쪽으로 순서대로 채워진 트리인 Complete Binary Tree(완전 이진 트리) 가 있다(두 트리의 차이점을 알아두면 좋을 것 같다).
BST, Binary Search Tree(이진 탐색 트리)
◾ 정의
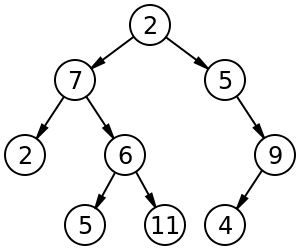
왼쪽 자식은 부모보다 작고 오른쪽 자식은 부모보다 큰 이진 트리
◾ 조건
1) 부모 노드의 왼쪽 노드는 부모 노드보다 작아야 한다.
2) 부모 노드의 오른쪽 노드는 부모 노드보다 커야 한다.
이진 트리의 일종으로 데이터를 저장하는 특별한 규칙으로 데이터를 저장하고 찾아낼 수 있다.
- 이진 탐색 노드에 저장된 값은 유일한 값이다.
- 루트 노드의 값은 왼쪽에 있는 모든 노드의 값보다 크다.
- 루트 노드의 값은 오른쪽에 있는 모든 노드의 값보다 작다.
- 각 서브 트리별로 2, 3번 규칙을 만족한다.
- 탐색/삽입/삭제 : O(logN)
- 최악의 경우.... O(N)
값이 추가되고 삭제되면서, 한 쪽에 치우친 '편향 트리'가 될 가능성이 있다.
=> 이를 해결하고자 Rebalancing이라는 기법으로 트리를 재조정한다.
+) 순회 종류
-
전위 순회(preorder traverse) : 뿌리(root)를 먼저 방문
뿌리 -> 왼쪽 자식 -> 오른쪽 자식
( 8 -> 1 -> 3 -> 6 -> 4 -> 7 ....) -
중위 순회(inorder traverse) : 왼쪽 하위 트리를 방문 후 뿌리(root)를 방문
왼쪽자식 -> 뿌리 -> 오른쪽 자식
( 1 -> 3 -> 4 -> 6 -> 7 -> 8 -> ...) -
후위 순회(postorder traverse) : 하위 트리 모두 방문 후 뿌리(root)를 방문
왼쪽자식-> 오른쪽 자식 -> 뿌리
(1 -> 4 -> 7 -> 6 -> 3 -> 13 -> ..)
높이 균형 이진 탐색 트리 (Adelson-Velsky and Landis, AVL 트리)
◾ 정의
스스로 균형을 잡는 이진 탐색 트리
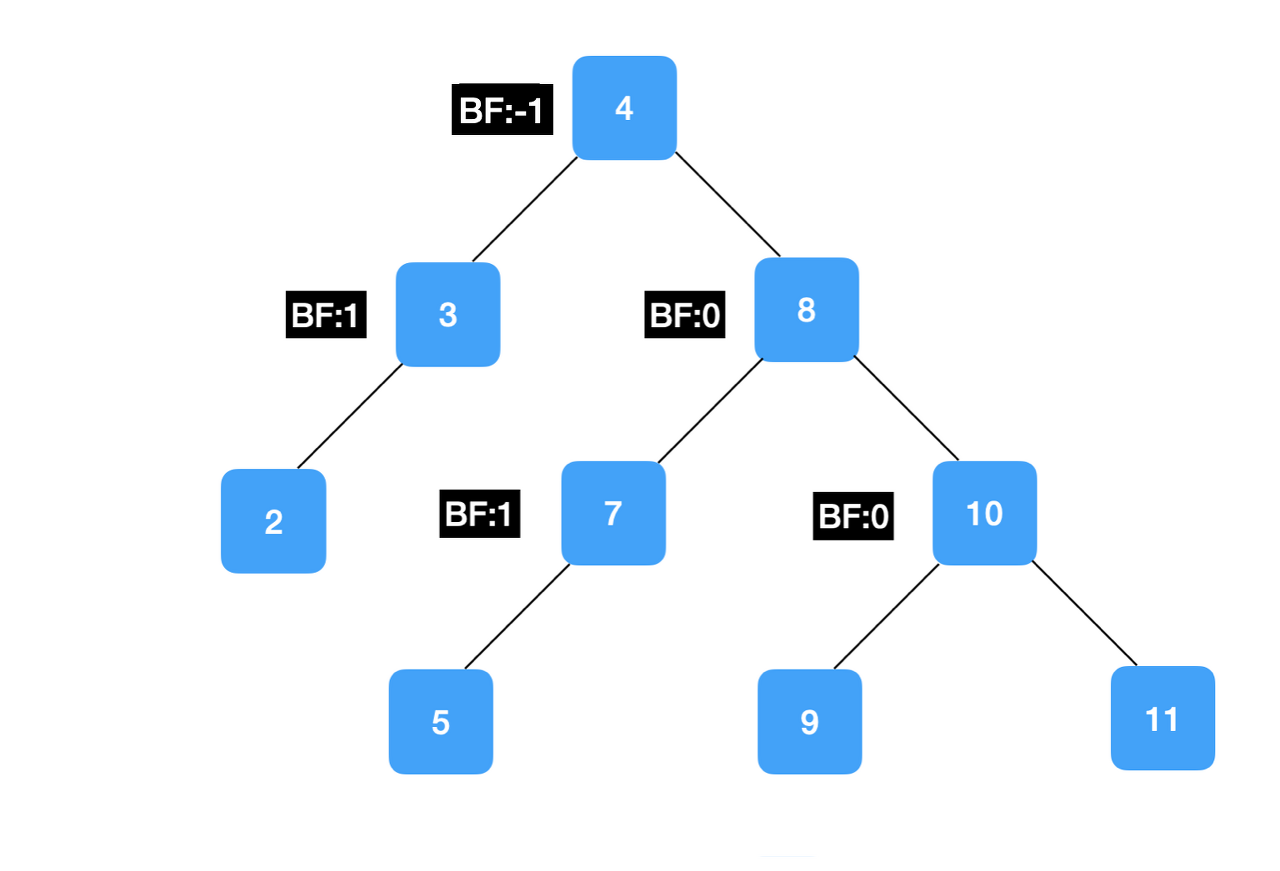
- 탐색/삽입/삭제 : O(logN)
- 최악의 경우 : O(logN)
- 균형을 잡는다는 것은 BF로 척대를 세우는데 여기서 삽입,삭제 연산을 수행할 때 트리의 균형을 유지하기 위해 LL- 회전, RR-회전, LR-회전, RL-회전 연산 등이 있다.
- BF : Balance Factor으로 왼쪽과 오른쪽의 자식 높이 차이를 뜻함
-> 균형이 잡혔다 = BF가 최대 1까지 차이나는 것.(-1 ~ 1
Red-Black 트리
◾ 정의
자가 균형 이진 탐색 트리

조건
- 모든 노드는 빨간색 혹은 검은색이다.
- 루트 노드는 검은색이다.
- 모든 리프 노드(NIL)들은 검은색이다. (NIL : null leaf, 자료를 갖지 않고 트리의 끝을 나타내는 노드)
- 빨간색 노드의 자식은 검은색이다.
== No Double Red(빨간색 노드가 연속으로 나올 수 없다) - 모든 리프 노드에서 Black Depth는 같다.
== 리프노드에서 루트 노드까지 가는 경로에서 만나는 검은색 노드의 개수가 같다.
🤔 AVL 트리와 RB 트리 중 왜 RB 트리를 더 많이 쓸까?
- AVL 트리는 균형을 엄격히 지키지만 RB 트리는 색상이 추가되어 여유롭게 균형을 유지하여 삽입, 삭제가 보다 더 빠르다.
- 이 둘은 시간이 소요되는 것은 O(log N)으로 같지만, RB 트리는 밸런싱이 AVL 트리에 비해 느슨하여 탐색은 불리하나 삽입 삭제가 빠르고, AVL 트리는 밸런스가 좀 더 엄격하여 탐색에 유리하다.
- BST의 최악의 경우의 예와 시간복잡도에 대해서 설명해주세요.
