[알고리즘] Minimun Spanning Tree 구현 - 백준 1197번

문제 (백준 1197번)

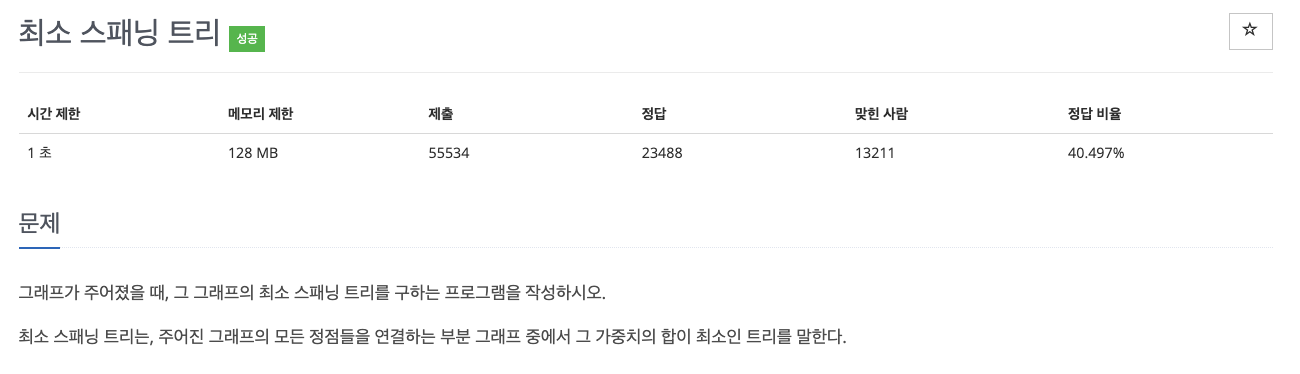
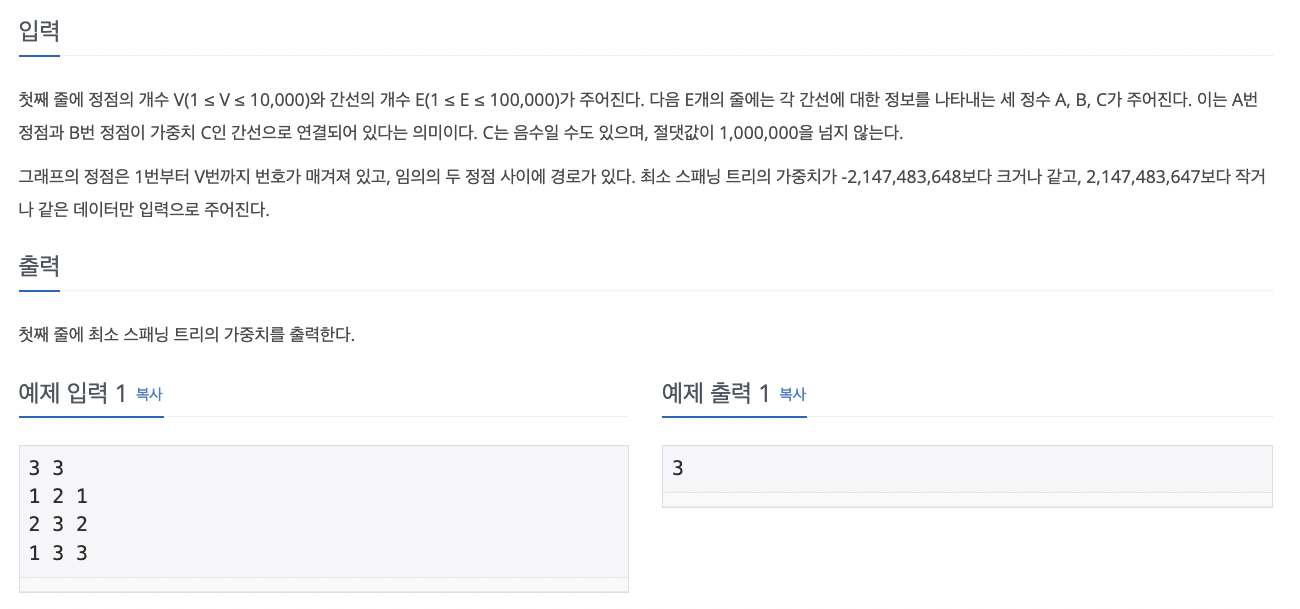
알고리즘 자체가 어려운 문제는 아니다.
vertex(정점)의 개수외 edge(간선)의 개수, 그리고 각 edge의 weight가 주어진 상황에서, minimum spanning tree의 weight를 출력하면 된다.

Kruskal 알고리즘과 Prim 알고리즘 모두 활용하였다.

kruskal 알고리즘

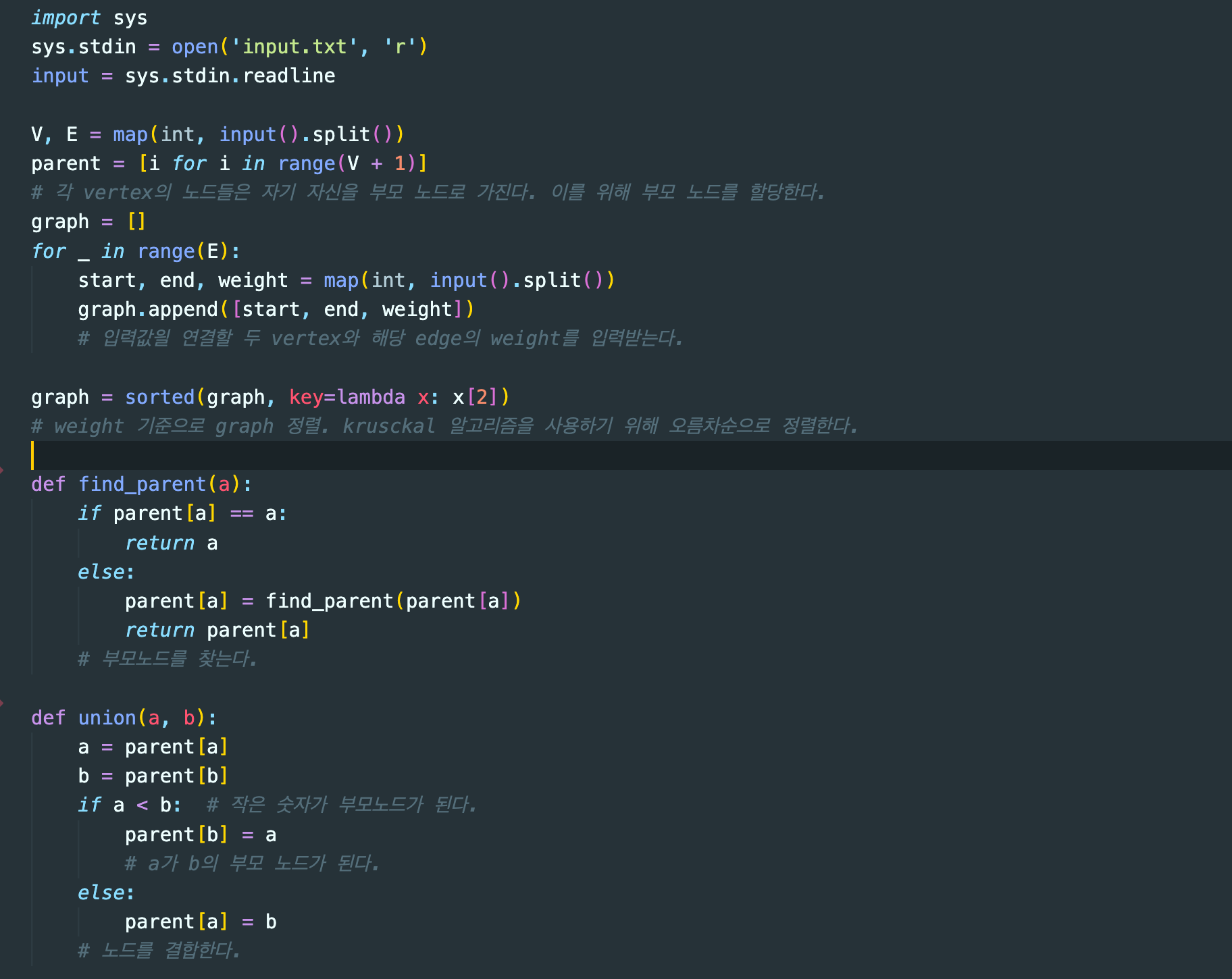
먼저 Kruskal 알고리즘으로 해결하였다.
각 주석에 어떠한 논리구조로 코드를 구현하였는지 작성하였지만 조금 더 첨언하자면,

1. 각 vertex의 노드들이 자기 자신을 부모 노드로 가지기 위해서 V+1개의 배열을 할당하였다. 이를 통해 0부터 V번까지 인덱스들이 만들어지고 이는 union-find 함수에서 노드들이 자기 자신을 부모 노드로 갖고 있는지 확인하는데 활용하였다.

2. 그래프를 weight기준으로 정렬한 것은 Kruskal 알고리즘의 특성때문이다. 해당 알고리즘의 기본적인 원칙은 사이클이 발생하지 않는 선에서 최솟값의 edge로 연결된 노드를 루트에 삽입하기 위함이다.

union-find 알고리즘을 이해하는 것이 쉽지 않았지만, 재귀를 통해 해당 노드의 root를 find하고 서로 다른 root를 가진 두 노드를 unify하는 방식으로 이해하였다.

Prim's 알고리즘

개인적으로 이해하는 것이 정말 어려웠다.

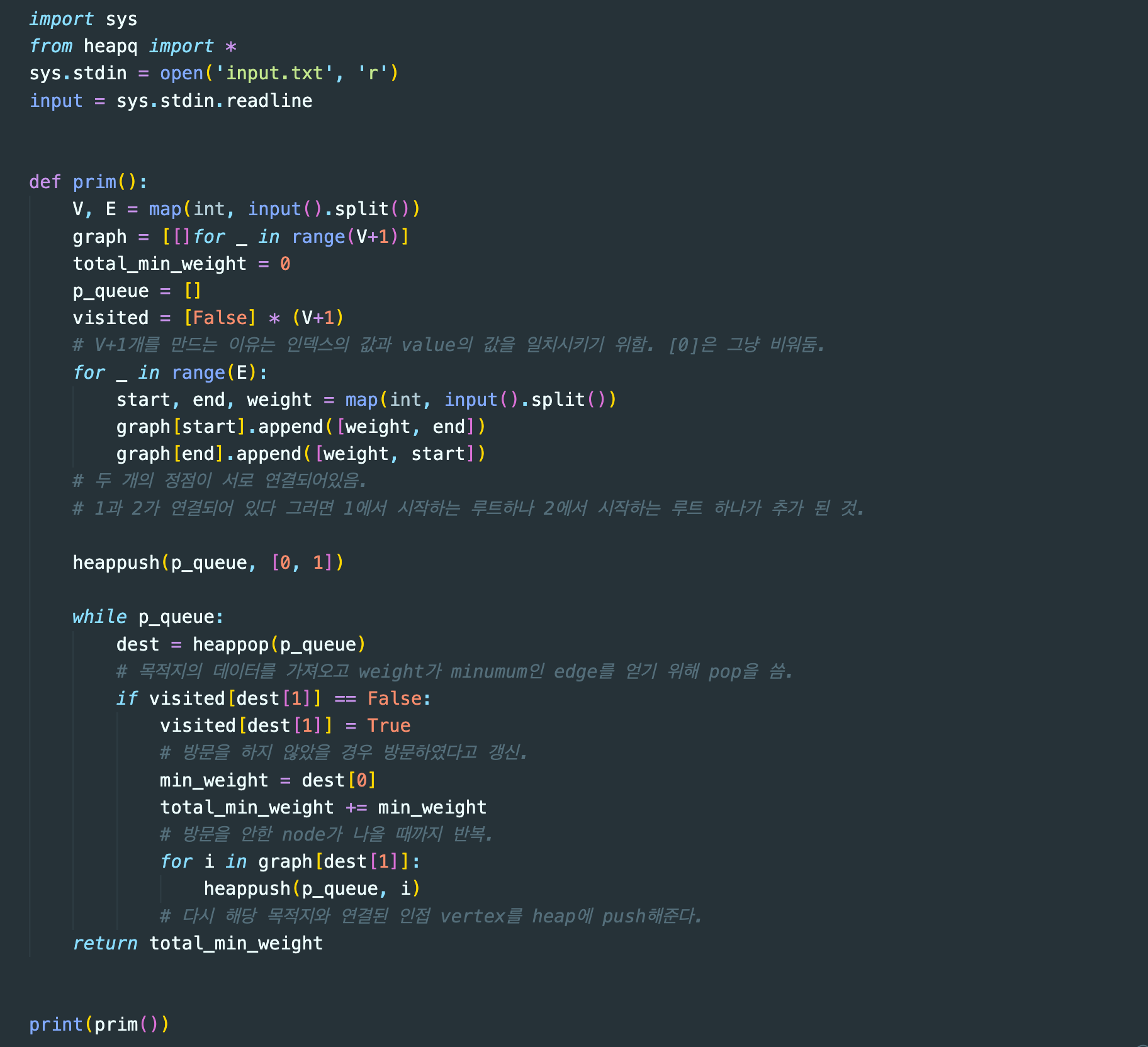
일단 입력값을 받는 것까지는 kruskal's 알고리즘하고 동일한 방식이다.
다만 차이점은 우선순위 큐의 특징을 활용하였다는 점이다.

우선순위 큐는 최소 값이나 최댓 값을 반환할 때 빠른 속도를 가진다.

이러한 점을 이용하여 weight를 기준으로 오름차순으로 정렬한 이후에 pop을 통해 이를 반환하는 방식을 채용하였다.