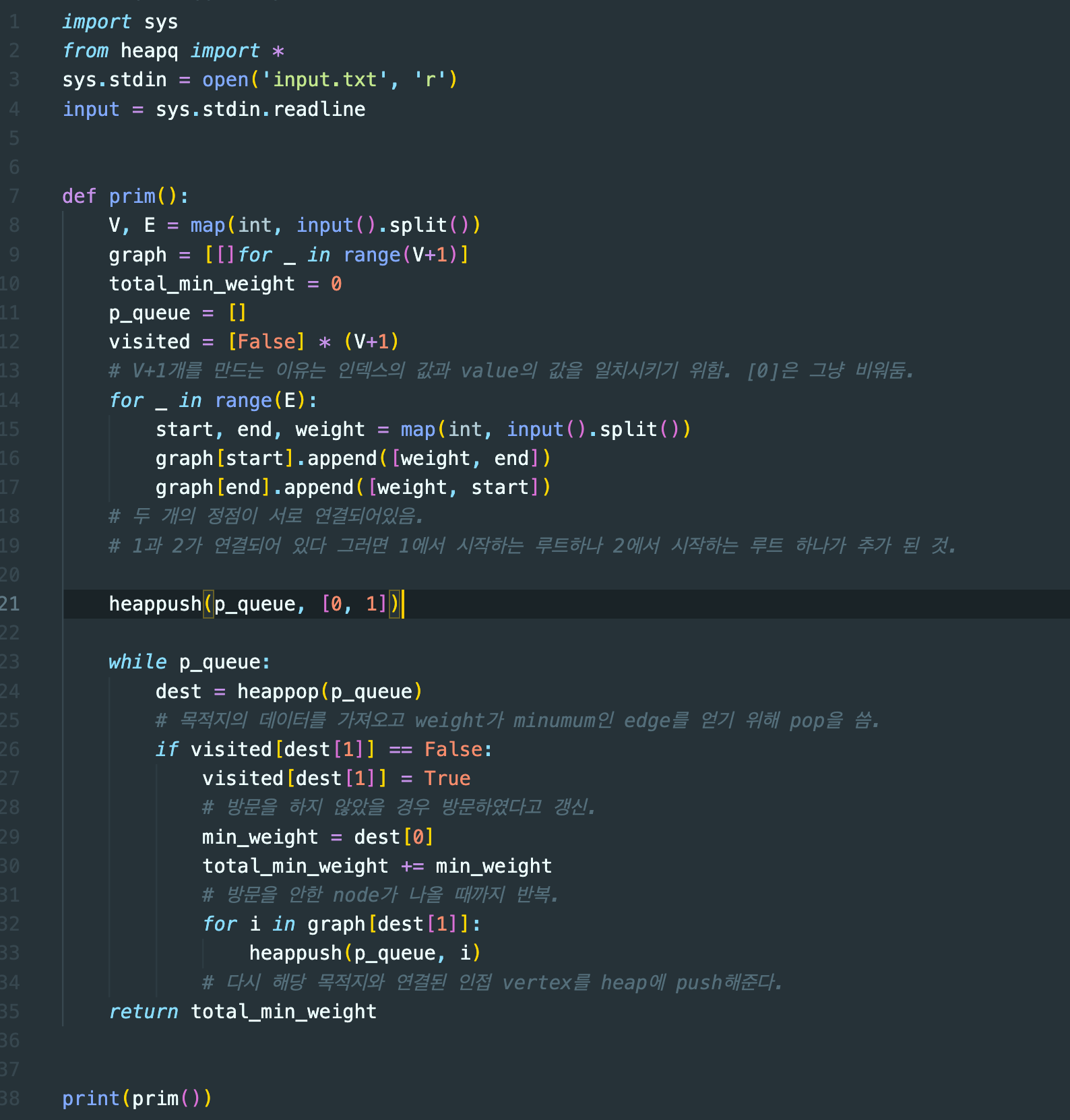
minimun spanning tree를 구하기 위한 알고리즘으로 Prim's Algorithm과 Kruskal's Algorithm이 있다.
Prim's Algorithm
프림 알고리즘은 그래프에 연결된 vertex주변에 있는 edge의 weigh의 최솟값을 골라 minimun spanning tree를 만들어내는 알고리즘이다.
구현은 다음과 같은 단계로 이루어진다.
- 임의로 한 개의 vertex를 선택하여 해당 vertex를 root node로 삽입하여 minimun spanning tree를 초기화한다.
- 해당 vertex를 다른 새로운 vertex에 연결하는 모든 edge를 찾고 그중 최솟값을 tree에 추가한다. (단 사이클이 형성되어서는 안된다.)
- minimum spanning tree를 완성할 때까지 2단계를 반복한다.
예시
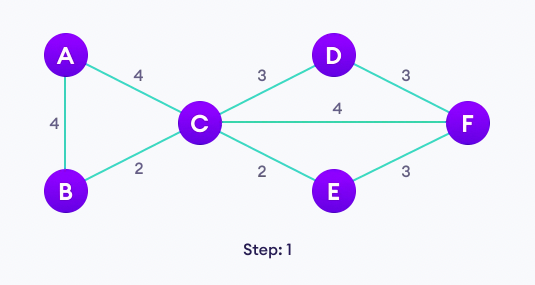
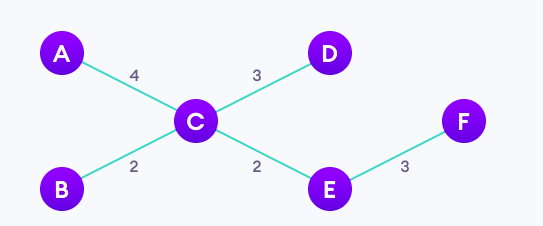
위 그래프의 minimum spanning tree를 구해보자.
먼저 임의로 한 개의 vertex를 선택하여보자.

가장 많은 edge로 연결된 C를 선택하였다.
이 vertex를 root node로 삽입하여 minimun spanning tree를 초기화한다.
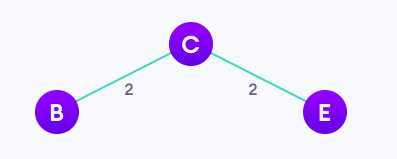
- 해당 vertex에 연결되어있는 vertex중 weight가 가장 작은 edge와 연결되어 있는 B와 E를 트리에 연결하였다.
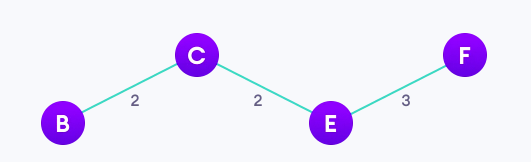
- C, B, E에 연결되어있는 vertex중 weight가 가장 작은 edge와 연결되어 있는 F를 트리에 연결하였다.
- 위와 같은 과정을 반복하면 아래와 같이 minimun spanning tree가 완성된다.
Kruskal's Algorithm
그래프 내의 모든 edge의 weight를 확인하고 가장 작은 weight부터 확인하여 minimum spanning tree를 만드는 알고리즘이다.
다음과 같은 방식으로 진행된다.
1. 그래프 내의 모든 edge의 weight를 오름차순으로 정렬한다.
2. 오름차순으로 정렬된 weight를 순회하면서 minimum spanning tree에 삽입한다. (사이클이 형성되지 않아야 함)
해당 알고리즘에서 사이클을 확인하기 위해 분리집합을 사용한다.
분리집합은 다음과 같은 특징을 가진다.
- 전체 집합 U에 대해 A, B는 U의 부분집합이다.
- A, B는 공통 원소를 가지지 않는다.
- A, B의 합집합이 곧 전체집합 U이다.
즉 edge로 연결된 vertex는 같은 집합. 그렇지 않은 경우 서로 다른 집합이다.
이미 같은 집합에 속해있는 vertex끼리 연결될 경우 사이클을 형성하게 된다.
이러한 방식을 사용하여 사이클 여부를 확인하고 방지할 수 있다.
이러한 방식의 알고리즘을 union-find 알고리즘이라고 하며, 해당 알고리즘을 통해 이미 동일한 루트를 갖고 있는 노드들은 이미 연결된 노드들임을 확인하고 weight를 더하지 않는다.
Kruskal's 방식 또한 Prim 방식과 유사하게 최소의 weight를 가진 edge와 연결된 노드를 루트에 삽입한다는 점이 있지만.
내가 생각하기에 근본적인 차이점은
- 사이클을 방지하기 위해 사용하는 알고리즘
- 최솟값의 weight를 찾기위해 어떠한 방식을 사용하는가
위 2가지라고 생각한다.
