문제

풀이
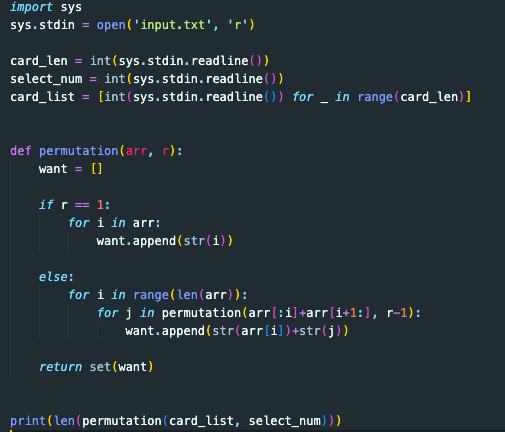
해당 문제는 재귀함수, 순열조합, 브루트포스 탐색, 배열, set()함수에 대한 지식을 활용하였다.
참고한 자료는 다음과 같다.
https://velog.io/@insutance/Python-set-%EC%9D%B4%EB%9E%80
set()함수
https://velog.io/@supergangho/2-Python-%EC%A1%B0%ED%95%A9-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98%EB%B8%8C%EB%A3%A8%ED%8A%B8%ED%8F%AC%EC%8A%A4
브루트포스(완전 탐색)을 통한 조합
코드 분석
입력 값 받기
card_len = int(sys.stdin.readline()) >> 전체 카드 수
select_num = int(sys.stdin.readline()) >> 뽑을 카드 수
card_list = [int(sys.stdin.readline()) for _ in range(card_len)]
>> 뽑은 카드 수 만큼 카드의 숫자를 입력
재귀함수를 학습하기 위해 itertools 라이브러리를 활용하지 않고 직접 순열 조합을 구현하는 함수를 작성하였다.
코드의 작동 방식
예시를 위해 배열 [1,2,3,4,5] 에서 숫자 2개로 이루어진 순열조합을 출력해보자
먼저 1을 먼저 뽑는다고 가정해보자
( 1 , 2 ) , ( 1 , 3 ) , ( 1 , 4 ) , ( 1 , 5 )
1을 제외한 나머지 숫자들을 활용해서 조합이 이루어진다. 이렇게 반복되면
( 3 , 1 ) ... ( 4 , 5 ) ... ( 5 , 4)
이와 같이 조합이 완성될 것이다.
이를 코드를 통해 컴퓨터에게 우리가 원하는 일을 맡겨보도록 하자.
def permutation(arr , r) > arr은 배열, r은 배열에서 뽑을 요소의 개수문제에 맞춰서 이야기하자면 우리가 가지고 있는 카드들은 1, 2, 3, 4, 5 총 5장이고 5장의 카드들로 이루어진 배열에서 2장, 즉 2개의 요소들로 이루어진 순열조합을 찾아내는 함수이다.
먼저
want = []숫자를 저장하기 위한 배열 want를 만들었다.
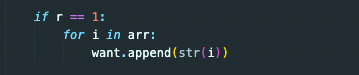
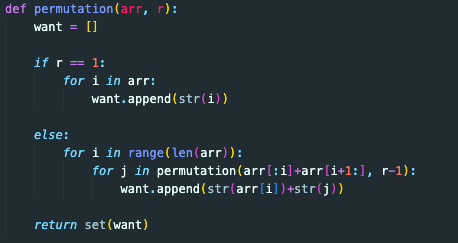
r 즉 뽑을 카드가 한 장 밖에 없다는 것은 한 개의 요소들로 이루어진 순열조합들만 완성 될 수 밖에 없기 때문에 want라는 배열에 우리의 카드배열의 숫자들을 하나씩 넣어준다는 것을 의미한다.
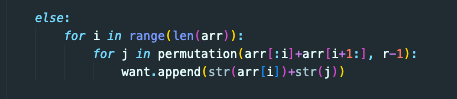
카드 배열의 숫자 범위 안에서, 예시로 말하자면 우리가 가지고 있는 카드는 1, 2, 3, 4, 5 총 5장이기 때문에 5번 반복할 것이다.
여기서 재귀함수를 호출하게 된다.
for j in permutation(arr[:i]+arr[i+1:], r-1):
want.append(str(arr[i])+str(j))permutation(i까지 요소들과 i+1까지의 배열, 그리고 뽑는 횟수를 1 감소)
이 의미는 이미 앞에서 앞에서 5장의 카드 중의 한 장을 선택하였다면, 앞으로 뽑을 카드는 해당 카드를 제외한 카드들을 뽑는다는 것을 의미하며
뽑는 횟수를 1 감소하는 이유는 우리가 뽑을 카드는 총 2장으로 하였고, 이미 1장의 카드를 뽑았기 때문에 앞으로 뽑을 수 있는 횟수는 한 번 밖에 없기 때문이다.
만약 우리가 5장의 카드를 4번 뽑는다고 생각하면
<남은 카드 5개 뽑은 횟수 0회 뽑은 카드 0회>
1 : 남은 카드 4개 뽑은 횟수 1회 뽑은 카드 1개 남은 횟수 3회
2 : 남은 카드 3개 뽑은 횟수 2회 뽑은 카드 2개 남은 횟수 2회
...
4 : 남은 카드 1개 뽑은 횟수 4회 뽑은 카드 4개 남은 횟수 0회
이런 식으로 이루어 지게 될 것이다.
다시 돌아와서
우리는 [ 1, 2, 3, 4, 5] , 2번이라는 인자를 순열 함수에 넣었다.
일단 당연히 남은 횟수는 2회이기 때문에
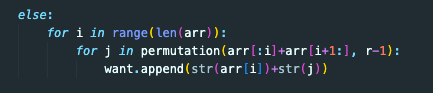
해당 함수가 실행될 것이고
앞서 얘기한대로 5번 반복되고 (for i in range(len(arr)))

그러면 해당 파라미터를 가진 permutation 함수가 다시 호출 될 것이다.
계속 자기 자신을 호출하여 오기 때문에 특정한 조건을 설정하여 두지 않으면 무한하게 호출된다.
여기서 똑같은 함수를 다시 실행되지만 인자는 다르다 아까 호출한 파라미터의 인자는
permutation(arr[:i]+arr[i+1:], r-1):이것이 의미하는 것은 i 전까지의 요소와 i+1부터 끝까지의 요소를 의미한다.
예를 들면 내가 2를 뽑았으면 2의 인덱스는 2 = arr[1]이기 때문에 2가 위치한 인덱스 전까지의 요소 즉 [1] 을 의미하는 것이고, arr[i+1]은 그 이후부터 배열 끝까지 모든 요소를 의미한다.
그리고 남은 횟수는 r-1이고 우리는 맨 처음 목적은 2장을 뽑는 것이었기 때문에 1을 뺀 1회가 인자가 된다.
그러면
permutation([1,3,4,5], 1)가 실행된다고 이해하면 될 것이다.
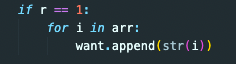
그러면 want에 해당 문자가 들어가게 되고 want[1, 3, 4, 5]가 될 것이다.
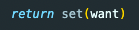
그리고 해당 값을 리턴 받게 된다. 중복된 값이 없으니 그대로 [1, 3, 4, 5]를 리턴 받게 된다.
여기서 끝나는 것이 아니다.
재귀 함수인 점을 유의하자!!!!!

여기 부분을 수행해서 호출된 함수를 계산한 것이고
그러면 아까 리턴받은 [1, 3, 4, 5]의 요소가 반복되어 투입될 것이다.

해당 함수의 want와 그 전에 호출된 함수의 want는 다르다. 왜냐 함수 안에서 실행된 지역변수이기 때문이다. 이 정도는 나도 알기에 굳이 적지는 않겠다.
그러면 맨처음 arr을 기억할 것이다.
[1,2,3,4,5]
그리고 우리는 2를 뽑은 상황을 가정했기 때문에 arr[2]인 상황이고
문자열 2와 want[0] 문자열 1을 합치면 21
문자열 2와 want[1] 문자열 3을 합치면 23
...
문자열 2와 want[3] 문자열 5를 합치면 25
가 완성되고 이를 want에 다시 저장하게 된다.
arr[0] 부터 계속 반복되게 되면
구성될 수 있는 모든 구성 조합이 want에 들어가게 될 것이다.
왜 set를 넣었는가?
예시에서는 1, 2, 3, 4, 5처럼 각각 다른 숫자였기 때문에 문제가 되지 않으나,
실제 문제에서 입력되는 값은 동일한 숫자의 카드가 입력된다.
그렇기 때문에 일단 모든 구성조합을 want에 넣은 이후 set()함수를 사용하여 중복값을 모두 없애야 한다.
그렇게 한 뒤에 해당 함수의 length를 출력하면 해당 순열조합의 개수를 알 수 있게 된다.
