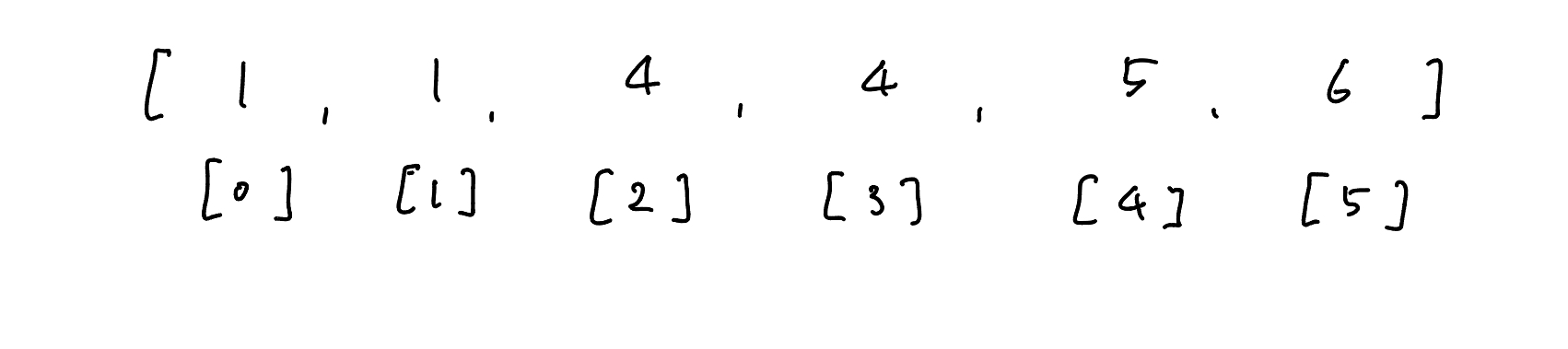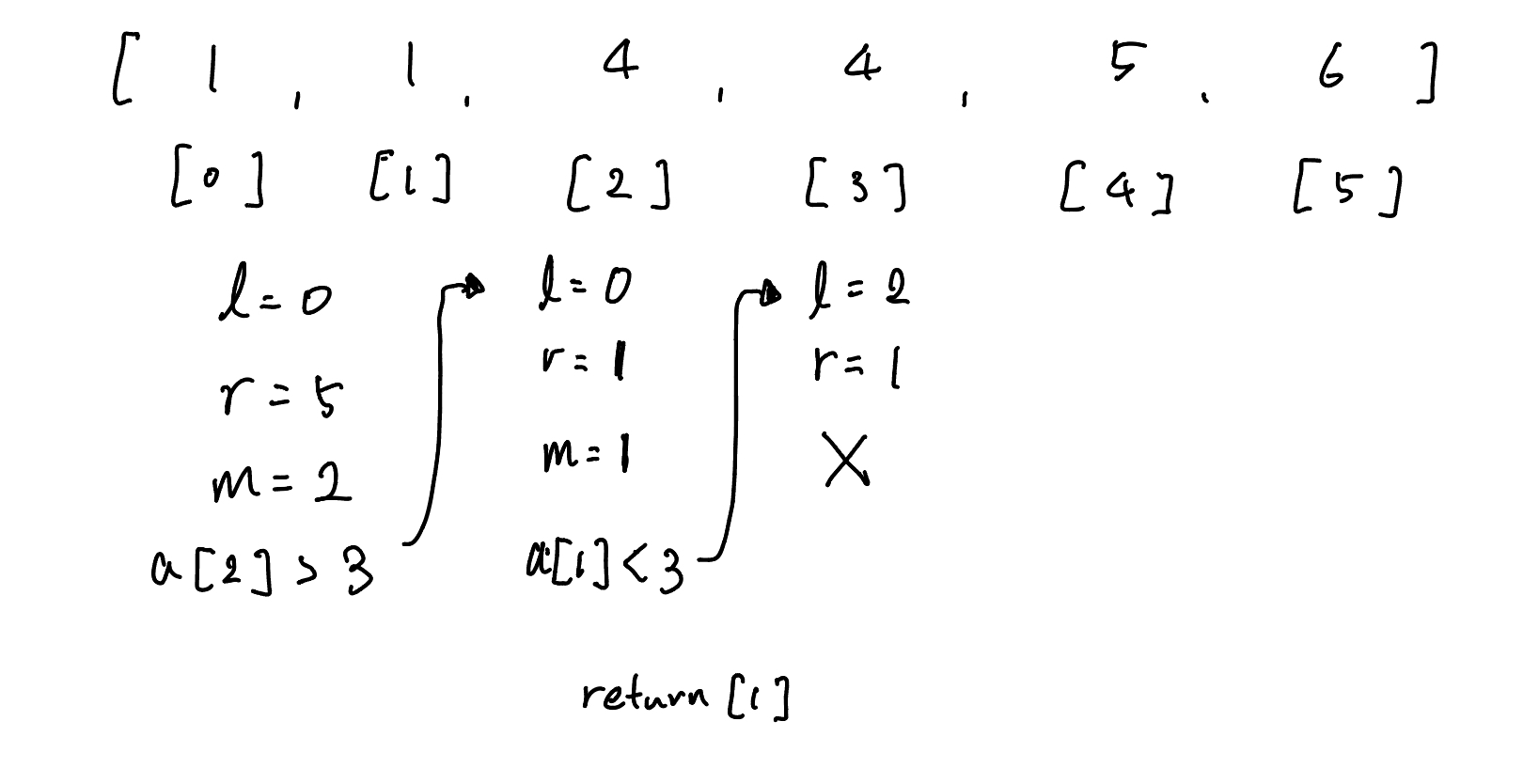[알고리즘] Binary Search (Lower Bound, Upper Bound)

Binary Search(이분 탐색)이란 정렬된 배열 내에서 목표 값의 위치를 찾는 검색 알고리즘의 일종이다.
1.
대상 값을 배열의 중간 요소와 비교하여 이 값이 동일하지 않으면 대상이 있을 수 없는 절반을 제거하고 나머지 절반을 검색하는 방식을 반복하여 목표 값을 찾는다.
2.
작은 배열을 제외하고는 선형방식보다 빠른 처리 속도를 가진다
3.
배열에 없는 경우에도 대상에 비해 배열에서 다음으로 작거나 다음으로 큰 요소를 찾는 문제를 해결하는 데에도 활용할 수 있다.

def binary_search(arr, target):
    start, end = 0, len(arr)

    while start <= end:
        mid = (start + end) // 2
        if arr[mid] == target:
            return mid
        if arr[mid] > target:
            end = mid - 1
        else:
            start = mid + 1

arr = [1, 2, 3, 4, 5]
result_idx = binary_search(arr, 3)
print(res, arr[res_idx])
# 3 2

위와 같이 정렬된 배열에 원하는 값을 찾으려고 할 경우 배열에서 중간 값을 정하여 해당 중간 값이 찾으려는 값과 같을 경우 바로 return, 더 작을 경우 배열의 끝 지점을 mid -1로 줄이거나 반대로 클 경우 시작 지점을 mid+1로 줄일 수 있다.

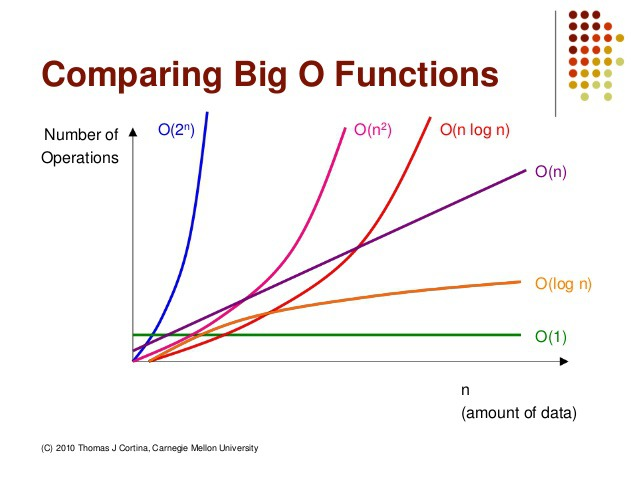
이분 탐색의 계산 복잡도는 O(logn) 이고 순차 탐색의 계산 복잡도는 O(n)이다. 대부분의 경우 훨씬 좋은 처리 속도를 가진다.

활용 문제 1 - 백준 1920번

풀이 과정)

이분 탐색 함수를 구현하였다.
앞서 말한 과정과 동일한 알고리즘으로 구성하였고
target이 있으면 return 1 없으면 return 0 을 하도록 하였다.

기본적으로 이분 탐색은 정렬이 되어야 하는데
아래의 리스트는 정렬을 하게 될 경우 출력 값이 원하는 대로 나오지 않기 때문에
탐색 대상인 N리스트를 정렬하였다.

반복문을 통해 M리스트의 요소를 넣었고 해당 요소가 정렬된 N리스트와 함께 인자로 들어가게하였다.

import sys
sys.stdin = open('input.txt', 'r')
input = sys.stdin.readline

N = int(input())
N_list = list(map(int, input().split()))

M = int(input())
M_list = list(map(int, input().split()))


def binary_search(arr, target):
    start = 0
    end = len(arr)-1
    mid = (start+end)//2

    while start <= end:
        if target == arr[mid]:
            return 1
        elif target > arr[mid]:
            start = mid + 1
        else:
            end = mid - 1
    return 0


N_list.sort()
for i in M_list:
    print(binary_search(N_list, i))

하지만 이와 같이 찾으려는 목표의 값이 명확하다면 쉽게 해결할 수 있지만, 이를 응용하여 원하는 값 이상이 처음 나오는 위치를 찾거나, 혹은 이를 초과하는 값이 처음 나오는 위치를 찾는 경우가 발생한다.
전자의 경우를 Lower Bound 후자를 Upper bound라고 한다.

Lower Bound를 활용하는 예시를 알아보자

배열 [ 1, 1, 4, 4, 5, 6 ] 에서 3 이상인 값이 처음으로 나타나는 위치를 찾는다고 가정

t_list = [1, 1, 4, 4, 5, 6]
target = 3
def l_bound(arr, target):
    l = 0
    r = len(arr)-1
    while l <= r:
        m = (l+r)//2
        if arr[m] == target:
            return m
        elif arr[m] > target:
            r = m-1
        else:
            l = m+1
    return m
print(l_bound(t_list, target))
## 1

실제로 3이상이 처음으로 나타나는 위치는 [2]인데 기존의 이분탐색으로 산출한 결과는 [1]이다.

해당 반복문을 다음과 같이 진행된다.

1번째 반복문에서는 l은 가장 배열에서 가장 작은 인덱스인 0을 r은 배열에서 가장 큰 인덱스를 찾기 위해 len(arr)-1인 5를 할당했다.

그렇게 중간값을 설정하고 맨 처음에 확인한 arr[2]는 4이므로 3보다 큰 값이다.
그래서 기존처럼 더 낮은 값을 확인하기 위해 r = m-1을 하여 다시 반복문을 하면 위와 같이 3은 배열에 존재하지 않기 때문에 반복하다 보면 l의 값이 r을 초과해버려서 반복을 탈출하고 그 전의 중간 값인 1을 출력하게 되는 것이다.

그러면 일단 문제점이 무엇인가

1. 목표 이상의 값이 처음으로 나타나는 위치를 찾기 위해서는 목표와 동일한 값이 나타났다고 해서 바로 return하면 안된다.

2. 해당 인덱스가 목표보다 크거나 같을 경우 경우 해당 인덱스가 같거나 큰 값이 처음 나오는 위치일 수도 있기 때문에 해당 인덱스도 포함을 해주어야 한다.

예시 리스트를 보면 arr[m]이 target보다 큰 상태에서 r=m+1을 하게되면서 4가 위치한 [2]를 포함하지 않는 문제가 발생하였다는 것을 참고하면 된다.

3. 위와 같은 문제점을 해결한 상태에서 반복문을 돌리게 되면 l과 r의 값이 동일한 상태에서 m의 값에서 변동없이 r에 할당되기 때문에 무한 반복이 진행된다.

위와 같은 문제점을 확인하고 코드를 작성해보자.

t_list = [1, 1, 4, 4, 5, 6]
target = 3


def l_bound(arr, target):
    l = 0
    r = len(arr)-1
    while l < r:
        m = (l+r)//2
        if arr[m] >= target:
            r = m
        else:
            l = m+1
    return r


print(l_bound(t_list, target))
# 2

위와 같이 3이상의 값이 처음으로 등장하는 위치를 찾을 수 있게 되었다.

Upper_bound는 처음으로 큰 값을 찾기위한 위치를 리턴해주는 알고리즘이다.
Lower_bound에서 큰 차이 없이 같은 값만 리턴 조건에서 제외하면 된다.

t_list = [1, 1, 3, 4, 5, 6]
target = 3


def l_bound(arr, target):
    l = 0
    r = len(arr)-1
    while l < r:
        m = (l+r)//2
        if arr[m] > target:
            r = m
        else:
            l = m+1
    return r


print(l_bound(t_list, target))
##