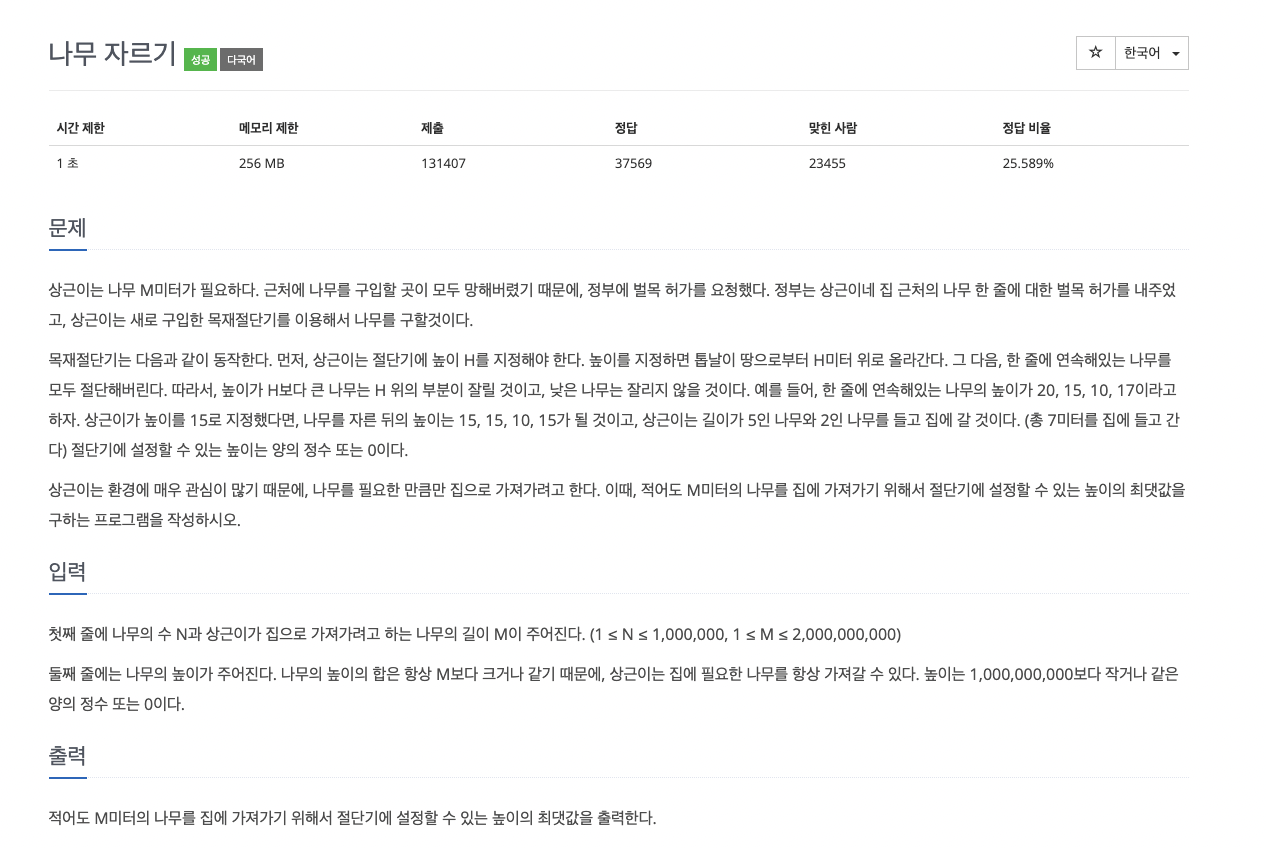
2805번
절단기에 설정할 수 있는 높이의 최댓값을 구한다.
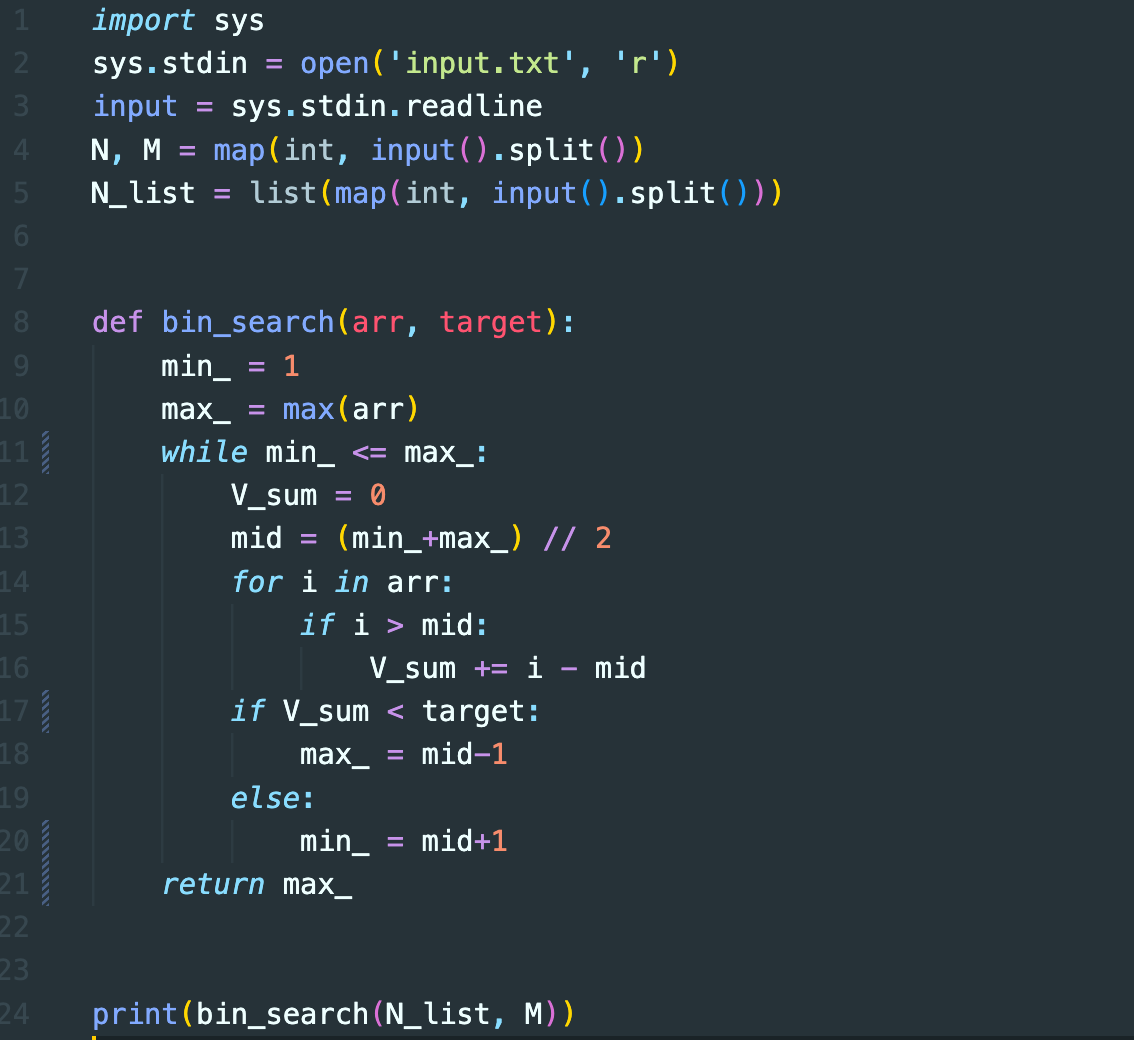
bin_search (리스트, 목표 높이의 최댓값)
절단기 높이 후보 리스트들을 나무의 최저 길이부터 최고 길이까지 다 넣어놓음
좌, 우, 가운데 인덱스 설정함
조건이 충족될 때 까지 무한 반복문
V_sum이라는 변수를 설정 > 총 자른 나무의 길의
i - cutlist[mid]는 각 나무들의 길이에서 나무를 자른 것
target이 V_sum과 같으면
해당 cut_list를 리턴함 ( 절단기 높이 )
작거나 크냐에 따라 인덱스를 절반으로 줄이는 이분 탐색을 시도함
그렇게 계속 반복해서
cult_list[mid]의 값을 리턴하도록함.
// 인덱스 말고 / 나무 자르는 길이를 맥스 나무 자르는 길이를 절반으로.. //
했는데 안됨 왜 안될까?
문제의 요지는 나무를 M미터이상의 나무를 가져가기 위해서 설치해야 하는 절단기 최대 높이를 구하는 문제이다.
문제를 풀면서 느낀 이분 탐색에서 중요한 것은
1. 탐색 종료 지점 설정
2. 이분 탐색에서 parameter 설정
3. 이분 탐색에서 어떠한 value를 찾을지
문제에서 원하고자 하는 값이 무엇인지 정확하게 판단해야 한다.
의사 코드로 생각해보자.
나무를 자를 수 있는 최솟값 = 1
최댓값은 나무들 중 가장 큰 나무최솟값이 최댓값을 넘지 않는 선에서 반복문
: 가져갈 수 있는 나무 높이 초기화
: 중간값 설정반복문) 나무들을 잘라보자
나무가 절단기 높이보다 작으면 못자름 (음수가 나오는 것이 아니라 0이 나와야함)
가져가야 할 나무들의 총합 += 절단기 - 나무높이만약 나무를 모은게 M미터보다 작으면
최댓값을 중간값 -1로 하고
M미터보다 크거나 같으면
최솟값을 중간값 +1로 하여 탐색 범위를 1/2로 줄여준다.이와 같은 반복을 진행하여 하나의 범위로 수렴한 상태에서 반복문을 종료하고
반환 받을 값은 최댓값이 된다.
최댓값을 반환받는 이유를 문제를 틀렸었던 이유와 함께 설명하고자 한다.
먼저 나무를 가져갈 수 있는 높이의 총합이 M미터와 같을 때 바로 해당 중간값을 반환받지 않은 이유는 문제에서 원하는 값이 M을 얻기 위한 절단기의 값이 아니라, M미터 이상을 얻을 수 있는 절단기의 총합을 원하기 때문이다.
절단기의 높이를 높이면 높일 수록 얻을 수 있는 나무의 높이 V_sum는 줄어들 수 밖에 없다. 그렇기 때문에 탐색의 최솟값과 최댓값의 설정을 다음과 같이 설정하였다.
그리고 결국 얻고자 하는 것은 절단기 높이의 최댓값이기 때문에 반환 받는 것은 maxV이다.
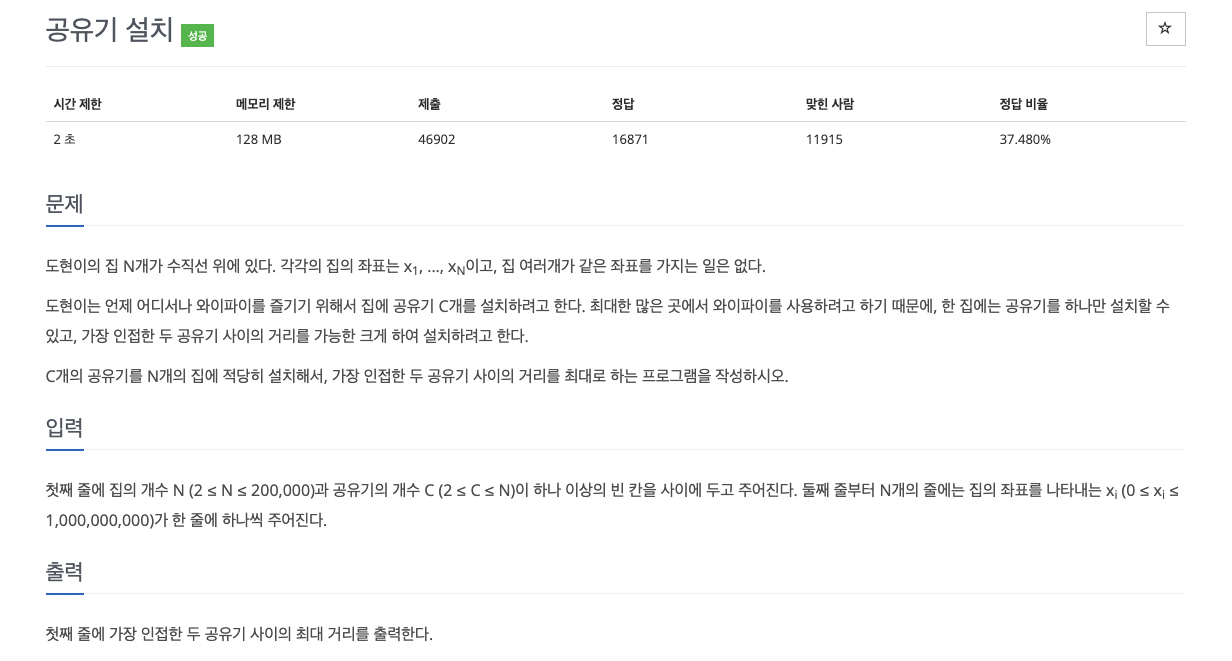
2110번
가장 인접한 두 공유기 사이의 최대 거리를 출력
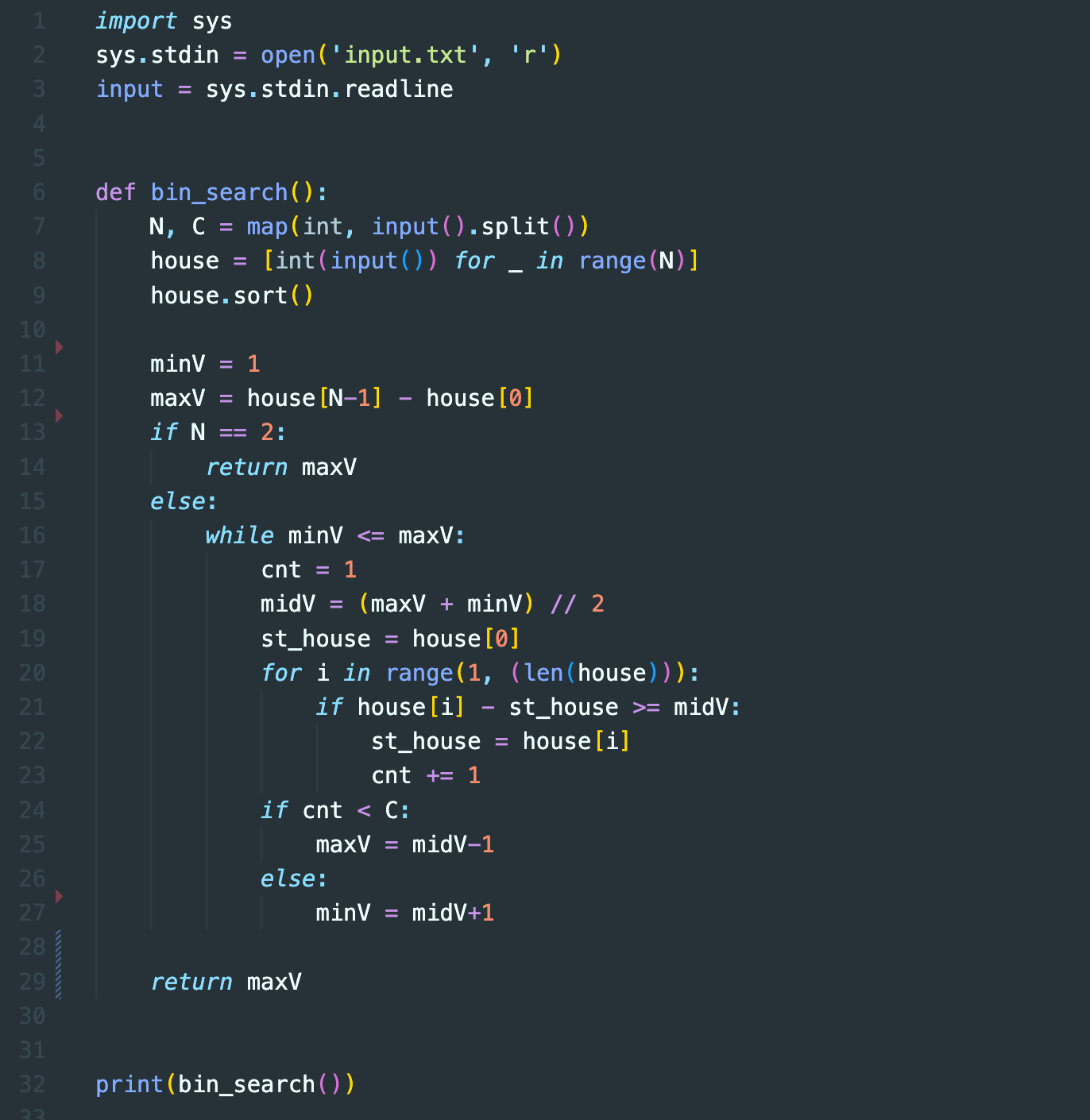
시행 착오 과정


문제에서 원하고자 하는 값은 공유기를 N개 설치할 수 있는 최대 거리이다.
사실 맨 처음에 가장 인접한 두 공유기 사이의 최대거리라고 하길래 문제를 이해하는데 조금 어려움이 있었는데
조금 고민해 보면서 느낀 점은 거리가 너무 멀면 공유기 설치를 다 못하고 거리가 너무 가까우면 할당된 공유기 보다 더 많은 공유기를 설치하여야 한다.
- 집 개수와 공유기 설치 개수, 집의 좌표를 입력받는다.
- 이분 탐색을 위해 집 좌표를 오름차순으로 정렬한다 (sort)
- 최솟값과 최댓값을 설정한다. 가능한 가장 가까운 거리는 1이 될 것이고, 최대 거리는 좌표 상 제일 끝 집과 첫번째 집이 될 것이다.
- 집이 2개면 최댓값을 바로 반환하면 된다.
- 아닐 경우가 문제임
5-1. 일단 반복문을 최솟값이 최댓값과 동일해질때까지 반복한다. 원하는 값은 배열에 있기 때문.
5-2. 공유기 설치한 갯수를 1로 한다. 이유는 맨 처음 집은 일단 설치할 거니까.
그리고 중요한 점이 하나 있다.
5-3. 각 집의 거리를 비교했을 때 지정 거리보다 작을 때는 설치하지 않고 그 다음 집과 비교하여야 하기 때문에 반복문을 할 때 기준 집을 요건을 충족하기 전에는 고정적으로 하여야 한다.
1번째 집과 2번째 집이 너무 가까워서 다음집을 비교할 때 1번째 집과 3번째 집을 비교해야지 2번째 집과 3번째 집을 비교해서는 안되기 때문이다.
5-4 공유기를 설치할 요건이 된다면 공유기 설치횟수를 +=1 한다.- 공유기 설치 개수가 더 적을 경우에는 거리가 너무 머므로 maxV = midV-1로 하고 공유기 설치 개수가 적거나 같을 경우 minV를 midV +1로 한다.
왜 공유기 설치개수가 딱 맞을 경우에 바로 return하지 않았냐면 역시 앞의 문제와 동일한 이유이다.
우리가 구해야 할 것은 해당 요건을 충족한 최댓값이기 때문에, 최댓값이 아니더라도 공유기를 맞게 설치할 경우가 발생할 수 있기 때문이다.
그러므로 우리는 수렴되는 최댓값을 반환받는 것이다.
