Summary

The Bisection Method

The Root-Finding Problem

• The problem of finding an approximation to the root of an equation can be traced back at least to 1700 B.C.E.
• A cuneiform table in the Yale Babylonian Collection dating from that period gives a sexigesimal (base-60) number equivalent to
  $1.414222$
  as an approximation to
  $\sqrt{2}$
  a result that is accurate to within $10^{-5}$.

The Bisection Method

Overview

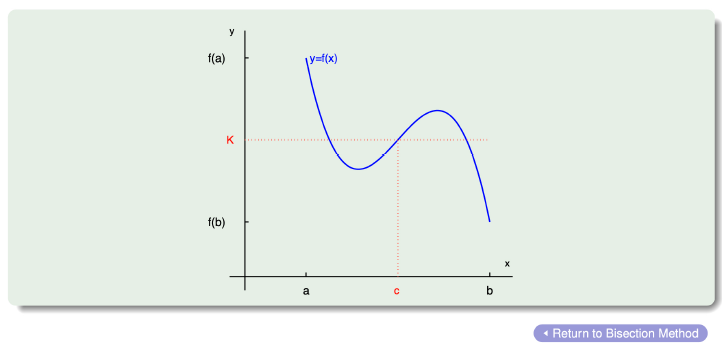
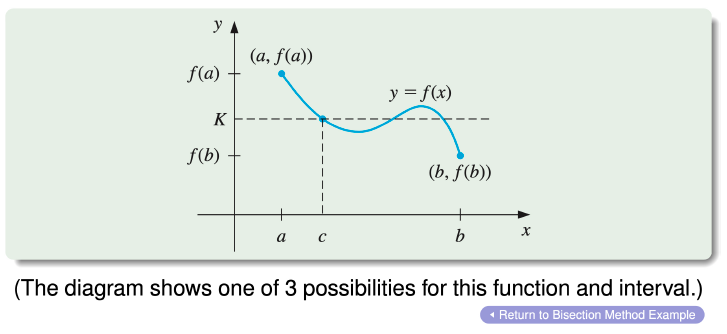
• We first consider the Bisection (Binary search) Method which is based on the Intermediate Value Theorem (IVT).
• Suppose a continuous function $f$, defined on $[a, b]$ is given with $f(a)$ and $f(b)$ of opposite sign.
• By the IVT, there exists a point $p \in(a, b)$ for which $f(p)=0$. In what follows, it will be assumed that the root in this interval is unique.

Intermediate Value Theorem

If $f \in C[a, b]$ and $K$ is any number between $f(a)$ and $f(b)$, then there exists a number $c \in(a, b)$ for which $f(c)=K$.

Bisection Technique

Main Assumptions

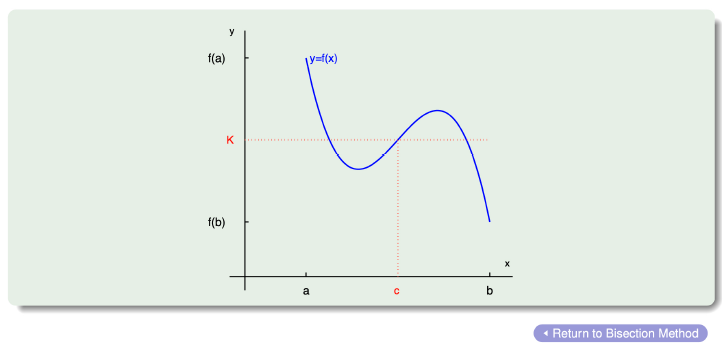
• Suppose $f$ is a continuous function defined on the interval $[a, b]$, with $f(a)$ and $f(b)$ of opposite sign.
• The Intermediate Value Theorem implies that a number $p$ exists in $(a, b)$ with $f(p)=0$.
• Although the procedure will work when there is more than one root in the interval $(a, b)$, we assume for simplicity that the root in this interval is unique.
• The method calls for a repeated halving (or bisecting) of subintervals of $[a, b]$ and, at each step, locating the half containing $p$.

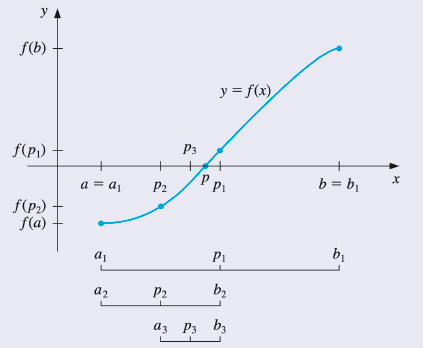
Computational Steps

To begin, set $a_1=a$ and $b_1=b$, and let $p_1$ be the midpoint of $[a, b]$; that is,

• If $f\left(p_1\right)=0$, then $p=p_1$, and we are done.
• If $f\left(p_1\right) \neq 0$, then $f\left(p_1\right)$ has the same sign as either $f\left(a_1\right)$ or $f\left(b_1\right)$.
  • If $f\left(p_1\right)$ and $f\left(a_1\right)$ have the same sign, $p \in\left(p_1, b_1\right)$. Set $a_2=p_1$ and $b_2=b_1$.
  • If $f\left(p_1\right)$ and $f\left(a_1\right)$ have opposite signs, $p \in\left(a_1, p_1\right)$. Set $a_2=a_1$ and $b_2=p_1$.

Then re-apply the process to the interval $\left[a_2, b_2\right]$, etc.

The Bisection Method to solve f(x)=0

Interval Halving to Bracket the Root

Given the function f defiend on [a,b] satisfying f(a)f(b) < 0.

The Bisection Method

Comment on Stopping Criteria for the Algorithm

• Other stopping procedures can be applied in Step 4.
• For example, we can select a tolerance $\epsilon>0$ and generate $p_1, \ldots, p_N$ until one of the following conditions is met:
  $\begin{aligned} \left|p_N-p_{N-1}\right| &<\epsilon \\ \frac{\left|p_N-p_{N-1}\right|}{\left|p_N\right|} &<\epsilon, \quad p_N \neq 0, \quad \text { or } \\ \left|f\left(p_N\right)\right| &<\epsilon \end{aligned}$
• Without additional knowledge about $f$ or $p$, Inequality (2) is the best stopping criterion to apply because it comes closest to testing relative error.

Solving $f(x)=x^3+4 x^2-10=0$

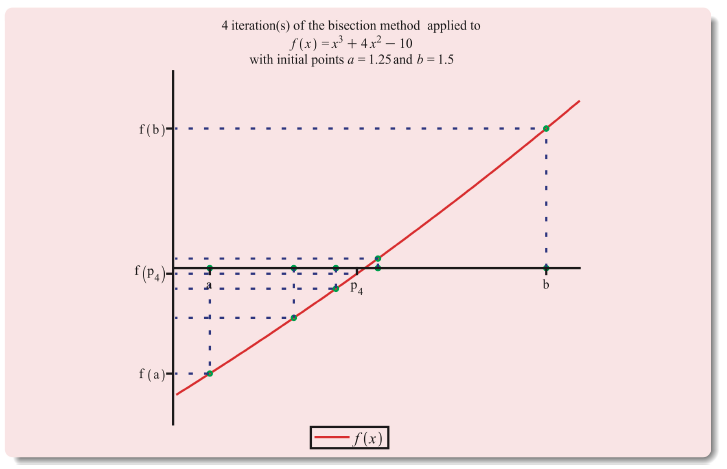
Example: The Bisction Method

Show that $f(x)=x^3+4 x^2-10=0$ has a root in $[1,2]$ and use the Bisection method to determine an approximation to the root that is accurate to at least within $10^{-4}$.

Relative Error Test

Note that, for this example, the iteration will be terminated when a bound for the relative error is less than $10^{-4}$, implemented in the form:
$\frac{\left|p_n-p_{n-1}\right|}{\left|p_n\right|}<10^{-4}$

Bisection Method applied to $f(x)=x^3+4 x^2-10$

Solution

• Because $f(1)=-5$ and $f(2)=14$ the Intermediate Value Theorem ensures that this continuous function has a root in $[1,2]$. -ivt
• For the first iteration of the Bisection method we use the fact that at the midpoint of $[1,2]$ we have $f(1.5)=2.375>0$.
• This indicates that we should select the interval $[1,1.5]$ for our second iteration.
• Then we find that $f(1.25)=-1.796875$ so our new interval becomes $[1.25,1.5]$, whose midpoint is $1.375$.
• Continuing in this manner gives the values shown in the following table.

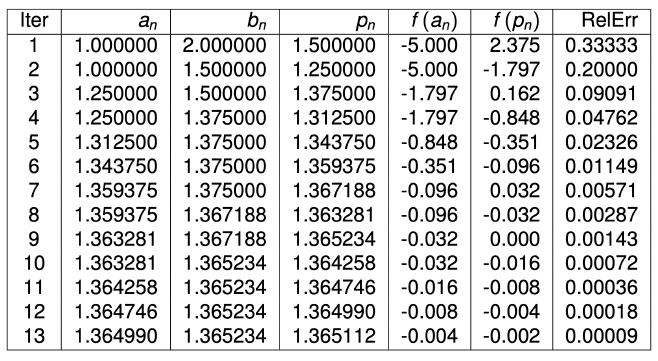
• After 13 iterations, $p_{13}=1.365112305$ approximates the root $p$ with an error
  $\left|p-p_{13}\right|<\left|b_{14}-a_{14}\right|=|1.3652344-1.3651123|=0.0001221$
  Since $\left|a_{14}\right|<|p|$, we have
  $\frac{\left|p-p_{13}\right|}{|p|}<\frac{\left|b_{14}-a_{14}\right|}{\left|a_{14}\right|} \leq 9.0 \times 10^{-5},$
  so the approximation is correct to at least within $10^{-4}$.
• The correct value of $p$ to nine decimal places is $p=1.365230013$

Intermediate Value Teorem

If $f \in C[a, b]$ and $K$ is any number between $f(a)$ and $f(b)$, then there exists a number $c \in(a, b)$ for which $f(c)=K$

Theretical Result for the Bisction Method

Theorem

Suppose that $f \in C[a, b]$ and $f(a) \cdot f(b)<0$. The Bisection method generates a sequence $\left\{p_n\right\}_{n=1}^{\infty}$ approximating a zero $p$ of $f$ with

Proof.

For each $n \geq 1$, we have

Since $p_n=\frac{1}{2}\left(a_n+b_n\right)$ for all $n \geq 1$, it follows that

Rate of Convergence

Because

the sequence $\left\{p_n\right\}_{n=1}^{\infty}$ converges to $p$ with rate of convergence $O\left(\frac{1}{2^n}\right)$; that is,

Conservative Error Bound

• It is important to realize that the theorem gives only a bound for approximation error and that this bound might be quite conservative.
• For example, this bound applied to the earlier problem, namely where
  $f(x)=x^3+4 x^2-10$
  ensures only that
  $\left|p-p_9\right| \leq \frac{2-1}{2^9} \approx 2 \times 10^{-3}$
  but the actual error is much smaller:
  $\left|p-p_9\right|=|1.365230013-1.365234375| \approx 4.4 \times 10^{-6}$

Example: Using the Error Bound

Determine the number of iterations necessary to solve $f(x)=x^3+4 x^2-10=0$ with accuracy $10^{-3}$ using $a_1=1$ and $b_1=2$.

Solution

• We we will use logarithms to find an integer $N$ that satisfies
  $\left|p_N-p\right| \leq 2^{-N}(b-a)=2^{-N}<10^{-3} .$
• Logarithms to any base would suffice, but we will use base-10 logarithms because the tolerance is given as a power of 10 .
• Since $2^{-N}<10^{-3}$ implies that $\log _{10} 2^{-N}<\log _{10} 10^{-3}=-3$, we have
  $-N \log _{10} 2<-3$ and $N>\frac{3}{\log _{10} 2} \approx 9.96$
• Hence, ten iterations will ensure an approximation accurate to within $10^{-3}$.
• The earlier numerical results show that the value of $p_9=1.365234375$ is accurate to within $10^{-4}$.
• Again, it is important to keep in mind that the error analysis gives only a bound for the number of iterations.
• In many cases, this bound is much larger than the actual number required.

Final Remarks

• The Bisection Method has a number of significant drawbacks.
• Firstly it is very slow to converge in that $N$ may become quite large before $p-p_N$ becomes sufficiently small.
• Also it is possible that a good intermediate approximation may be inadvertently discarded.
• It will always converge to a solution however and, for this reason, is often used to provide a good initial approximation for a more efficient procedure.

이분법은 많은 중요한 결점들을 가지고 있다.
첫째, p-pN이 충분히 작아지기 전에 N이 상당히 커질 수 있다는 점에서 수렴하는 것은 매우 느리다.
또한 좋은 중간 근사치가 실수로 폐기될 수 있다.
그러나 이는 항상 솔루션으로 수렴되며, 이러한 이유로 더 효율적인 절차를 위해 좋은 초기 근사치를 제공하는 데 종종 사용된다.