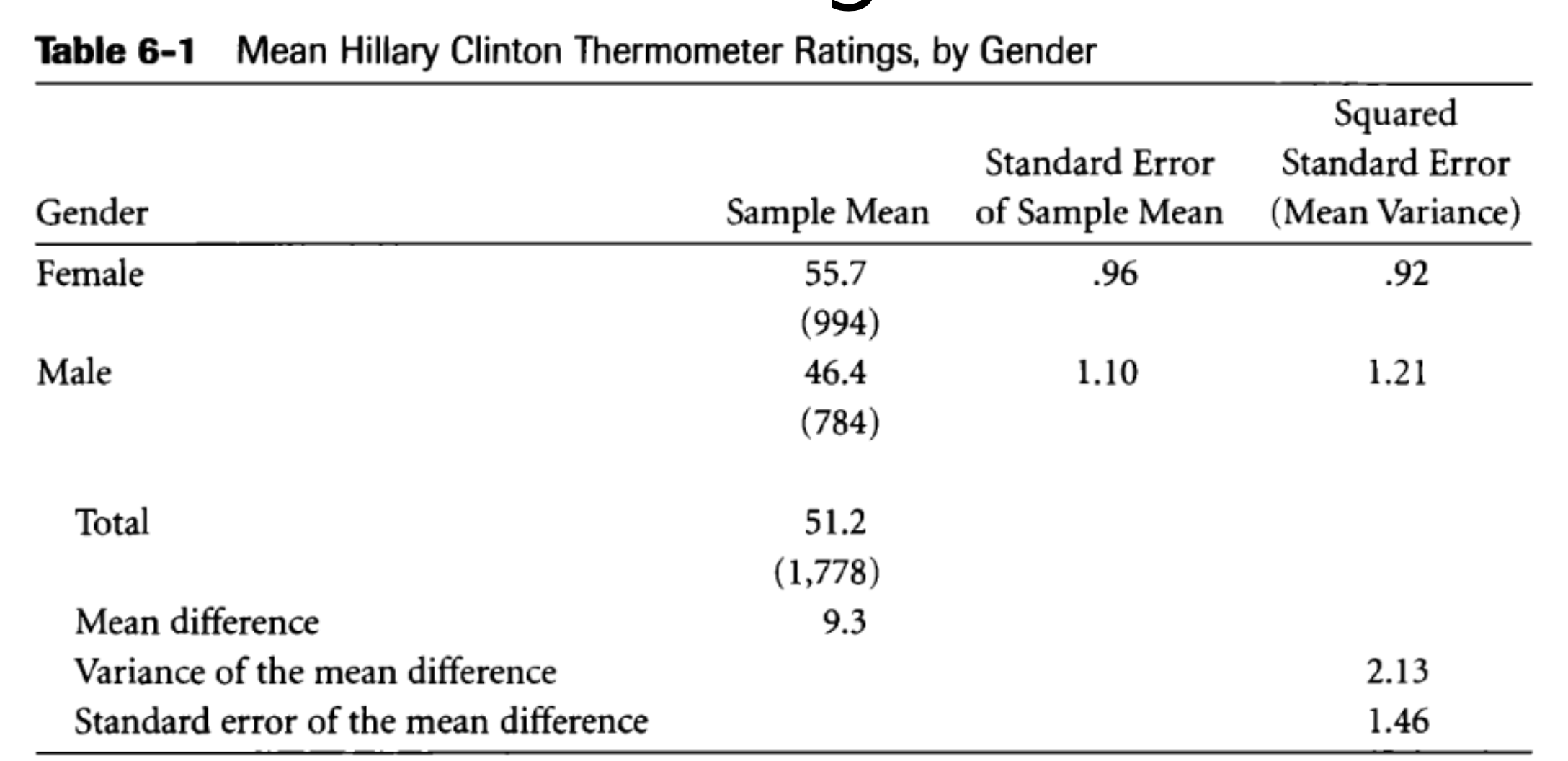
위의 그래프를 보면, 힐러리 클링턴에 대한 여성과 남성의 호감도를 볼 수 있다. 표본평균을 볼 때, 여성은 55.7%가 호감을 느끼고 남성은 그보다 작은 46.4%가 호감을 느낀다.
두 성별간의 평균적 호감도 차이를 대략 10%가 난다.
그런데 이것은 표본의 평균을 비교한 것이고, 실질적으로 모평균을 비교한 것이 아니다.
그렇다면, 실질적으로 호감도에 대한 두 성별의 모평균이 실은 별 차이가 없는 것 아닐까?
즉, 우연히 힐러리 클링턴에 대한 두 성별의 호감도 차이가 났을 가능성이 있지 않을까?
이러한 궁금증을 가지고 있다면, 두 표본평균의 유의성을 검정해볼 필요가 있다.
성별과 힐러티 클링턴에 대한 호감도가 사실 상관이 없다고 가정해보자.
이 경우, 두 성별의 표본평균이 우연히 발생했다, 이 두 표본 평균이 랜덤 샘플링 오차에 의해서 발생한 것이라고 생각하는 것이다. 이렇게 관찰된 값이 사실 랜덤 샘플링 오차에 의해 발생한 것이고, 사실 모평균에서는 다른 결과가 나올 것이라고 가정하는 것이 H0(Hypothesis 0), 귀무 가설이다.
즉, 귀무가설은 "효과가 없다" 또는 "두 그룹 간에 차이가 없다"와 같이 어떠한 효과나 차이가 존재하지 않는 상태를 설명합니다.
귀무 가설의 반대는, hypothesisA(대립가설)이다.
모수로부터 표본값이 충분히 멀리 떨어져있다면, (여기서 어느정도의 신뢰구간을 설정할지는 자유이지만 여기서는 95프로라고 가정한다.) 귀무가설을 reject할 수 있을 것이다. 즉, 관찰된 값은 랜덤 샘플링 오차에 의한 것이 아니라, 실질적으로 모수에서도 동일하거나 비슷한 결과가 나올 것이다.
이렇게 귀무가설을 설정해놓고 나면, 두 표본평균이 우연히 발생했는지 아닌지에 대해서 검정을 해봐야 한다. 그렇게 하기 위해서 t-test 검정을 해보겠다.
만약에 귀무가설이 옳다고 가정했을 때, 표본에서 귀무가설과 같은 값이 나올 가능성이 샘플링 100번 중에 5번보다 적다고 한다면, 우리는 귀무가설을 기각한다. 100번 중에 5번도 일어나지 않을 희박한 가능성이기 때문이다. 물론, 100번 중 5번이라는 기준은 이것은 전통적으로 이어지는 것이다. 100번 중에 1번이라고 가정해도 된다. 만약, 그 가능성이 샘플링 100번 중에 5번보다 많다고 하면, 귀무가설을 기각하지 못한다.
귀무가설이 두 표본 평균이 랜덤 샘플링 오차에 의해 발생한, 우연에 의한 것이라고 가정했으니, 두 표본 평균에 대한 검정 통계량을 가지고 검정을 진행해본다. 여기서 사용할 방법은 t-test이다. 이는 두 표본 평균의 차이를 표본 표준 오차로 나눈 값이다.
그리고 두 표본의 표본 오차 차이는 다음과 같다.
표에서 볼 수 있듯이, 두 표본 평균의 차이는 9.3(9.3 - 0)이고 두 표본 표준오차의 차이는 1.46이다. Z는 9.3/1.46으로 6.37이다.
한편, 이렇게 가설에 대한 검정을 할 때에는 오류가 발생할 수도 있다.
type 1 error와 type2 error가 존재한다.
type 1 error는 귀무가설이 맞는데 귀무가설을 reject를 했을때 발생하는 오류이다
type2 error는 귀무가설이 틀렸는데 귀무가설을 reject하지 않았을 때 발생하는 오류이다.
