Dynamic Programming (DP)
복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법으로, 부분 문제 반복과 최적 부분 구조를 가지고 있는 문제를 푸는데 효율적이다. (큰 문제를 작은 문제로 쪼개서 그 답을 저장해두고 재활용)
DP 사용 이유
같은 작은 문제들을 여러번 반복 계산하여 비효율적일 수 있는 경우 dp를 사용한다! 그 예로 대표적인 것이 피보나치 수열(fibo(n) = fibo(n-1)+fibo(n-2))이 있다. fibo(100)을 단순 재귀로 구현하면 살아 생전에 답이 나오지 않을 것이다...🥲 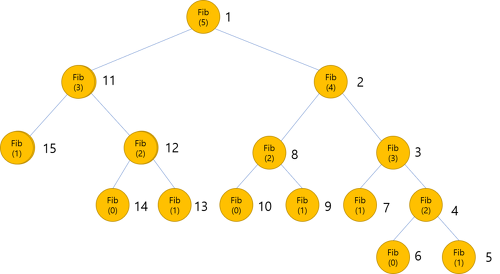
DP 사용을 위한 조건
DP를 사용하기 위해서는 다음 두가지 조건을 만족해야한다!
1. 부분 문제 반복 (Overlapping Subproblem) : 어떤 문제가 여러개의 부분 문제(Subproblem)으로 쪼개지는 경우
2. 최적 부분 구조 (Optimal Substructure) : 작은 부분 문제에서 구한 최적의 답을 합쳐 큰 문제의 최적의 답을 구할 수 있는 것
DP 사용 방법
DP 문제를 풀 때 어렵다면, 다음 과정을 따라가보자!
-
DP로 풀 수 있는 문제인지 확인!
: 보통 특정 데이터 내 최대/최소 계산을 하거나 특정 조건 내 데이터를 세야 한다거나 확률 등의 계산의 경우 DP로 풀 수 있는 경우가 많다고 한다. -
점화식 만들기 (변수 간 관계 정의)
-
Tabulation / Memoization (계산 결과를 저장해 두었다가 이용하여 중복 계산을 줄이는 방식)
-
기저 상태(문제가 정의되는 최소한의 케이스) 파악
-
구현 (Bottom-Up, Top-Down 두가지 방식으로 구현 가능)
DP 구현
Bottom-Up
- Tabulation, 반복문 이용
- 밑에서부터 계산을 수행하고 누적시켜서 전체 큰 문제를 해결하는 방식
int fiboData[100] = {0,};
int fibo(int n) {
fibodata[0] = 0;
fiboData[1] = 1;
for (int i=2; i<=n; i++)
fiboData[i] = fiboData[i - 1] + fiboData[i - 2];
return fiboData[n];
}Top-Down
- Memoization, 재귀 이용
- 위에서부터 호출을 시작하여 밑까지 내려간 다음 해당 결과 값을 재귀를 통해 전이시켜 재활용하는 방식
int fiboData[100] = {0,};
int fibo(int n) {
if (n<=2)
return 1;
if (fiboData[n]==0)
fiboData[n] = fibo(n-1) + fibo(n-2);
return fiboData[n];
}다른 알고리즘과의 차이점
-
그리디 알고리즘과의 차이점
동적 계획법은 모든 방법을 일일이 검토하여 최적의 해를 찾아내는 방식으로, 그리디 알고리즘에 비해 오랜 시간이 걸리지만 결과적으로 항상 최적의 해를 구할 수 있다는 장점을 가지고 있다! -
분할 정복과의 차이점
분할 정복은 분할했을 경우 반복적인 문제가 발생하지 않지만, DP는 반복적인 문제가 발생하기 때문에 Memoization 기법들이 필요한 것이다!
