Greedy Algorithm

그리디 알고리즘은 DP 사용 시 지나치게 많은 일을 한다는 것에서 착안하여 고안된 알고리즘이다. Greedy는 ‘탐욕스러운, 욕심 많은’ 이란 뜻으로 Greedy 알고리즘은 말 그 대로 여러 경우 중 하나를 결정해야 할 때마다 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행하여 최종적인 해답에 도달하는 방법이다.

Greedy Algorithm 특징

• DP와 마찬가지로 주로 최적화 문제를 푸는데 사용
• 순간마다 하는 선택은 그 순간에 대해 지역적으로는 최적이지만, 그 선택들을 계속 수집하여 최종적(전역적)인 해답을 만들었다고 해서, 그것이 최적이라는 보장은 없다.
• 탐욕알고리즘을 적용할 수 있는 문제들은 지역적으로 최적이면서 전역적으로 최적인 문제들이다.

Greedy Algorithm 조건

탐욕 알고리즘이 잘 작동하는 문제는 대부분 탐욕스런 선택 조건(greedy choice property)과 최적 부분 구조 조건(optimal substructure)이라는 두 가지 조건을 만족된다. 아래 조건이 만족되는 경우 탐욕 알고리즘은 최적해를 구하지 못한다. 하지만, 이러한 경우에도 탐욕 알고리즘은 근사 알고리즘으로 사용이 가능할 수 있으며, 대부분의 경우 계산 속도가 빠르기 때문에 실용적으로 사용할 수 있다. 이 경우 역시 어느 정도까지 최적해에 가까운 해를 구할 수 있는지를 보장하려면 엄밀한 증명이 필요하다.

• 탐욕스런 선택 조건: 이전 선택이 이후 선택에 영향을 주지 않음
• 최적 부분 구조 조건: 문제에 대한 최적해가 부분문제에 대해서도 역시 최적해

대표적인 Greedy Algorithm

MST를 만들기위해 이용되는 프림 알고리즘(O(V^2))과 크루스칼 알고리즘(O(E log V))은 대표적인 그리디 알고리즘이다. (MST란 Minimum Spanning Tree의 약자로, 그래프에 있는 모든 정점을 포함하면서 가중치 총 합이 가장 작은 트리를 말한다.)

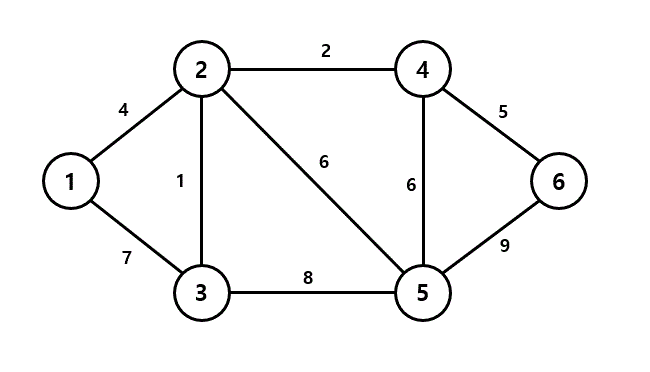
위 그래프의 MST는 다음과 같다.

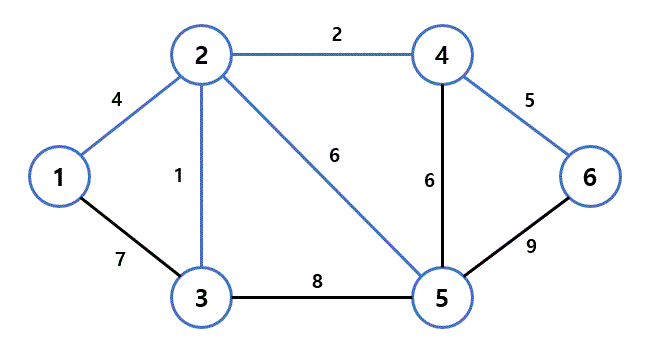
프림 알고리즘(Prim's Algorithm)

프림 알고리즘은 트리를 유지하면서 가중치가 낮은 간선을 선택해가는 방법이다.

1. 임의의 정점을 선택
2. 정점에 연결된 간선 중 가장 가중치가 작은 간선을 선택
3. 모든 정점이 선택될 때까지 반복

다음은 프림 알고리즘을 구현한 코드이다. 백준 1197번: 최소 스패닝 트리의 답이기도하다.

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

int V, E, a, b, c;
bool visit[10001];
vector<pair<int, int>> edge[10001];

int prim(){
    int ans = 0;
    priority_queue<pair<int, int>> pq;
    pq.push({0, 1}); // 1번 정점부터 시작
    while (!pq.empty()){
        int cost = -pq.top().first;
        int node = pq.top().second;
        pq.pop();
        if(visit[node]) continue;
        visit[node] = true;
        ans+=cost;
        for(int i=0; i<edge[node].size(); i++){
            cost = edge[node][i].first;
            if(visit[edge[node][i].second]) continue;
            pq.push({edge[node][i]}); // 현재 정점에서 이동 가능한 방문하지 않은 정점
        }
    }
    return ans;
}

int main(){
    ios_base::sync_with_stdio(0); cin.tie(0);
    cin >> V >> E;
    for(int i=0; i<E; i++){
        cin >> a >> b >> c;
        edge[a].push_back({-c, b}); // max heap to min heap 
        edge[b].push_back({-c, a});
    }
    cout << prim();
}

크루스칼 알고리즘(Kruskal's Algorithm)

크루스칼 알고리즘은 트리를 유지하며 만들어가는 것이 아니라, 트리를 마구 생성해서 잇는 기법이다. 따라서 임의의 정점을 선택했을 때, 그 정점이 어느 집합의 원소인지 알아내는 연산이 추가로 필요하다.

1. 모든 간선들의 가중치를 오름차 순으로 정렬
2. 가중치가 가장 작은 간선을 선택하고, 2개의 노드가 서로 연결되지 않은 상태라면 연결하는 과정을 반복 (union-find를 이용하여 구현 가능)

다음은 union-find를 이용하여 크루스칼 알고리즘을 구현한 코드이다. 백준 1197번: 최소 스패닝 트리의 답이기도하다.

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

int V, E, a, b, c, root[10001]{};
struct edge {int node1, node2, weight;}; // edge 구조체
bool compare(edge u, edge v) {return u.weight < v.weight;} // weight로 비교하여 오름차순 정렬
vector<edge> eg; //edge type 벡터

int find(int x){ // root를 찾음 
    if(root[x]==x) return x;
    return root[x] = find(root[x]); // 경로 단축
}

void union_(int x, int y){ // 정점 연결
    root[find(x)] = find(y);
}

int main(){
    ios_base::sync_with_stdio(0); cin.tie(0);
    cin>>V>>E;
    for(int i=1; i<=V; i++) root[i] = i; // union-find를 위한 초기화
    for(int i=0; i<E; i++){
        cin>>a>>b>>c;
        if(a!=b) eg.push_back({a,b,c});
    }
    sort(eg.begin(), eg.end(), compare); // 정렬
    
    int ans = 0;
    for(int i=0; i<eg.size(); i++){
        if(find(eg[i].node1)!=find(eg[i].node2)) { // 연결되지 않은 경우
            union_(eg[i].node1, eg[i].node2); // 연결
            ans+=eg[i].weight; // 연결된 weight를 답에 더해줌
        }
    }
    cout << ans;
}