Linear Regression

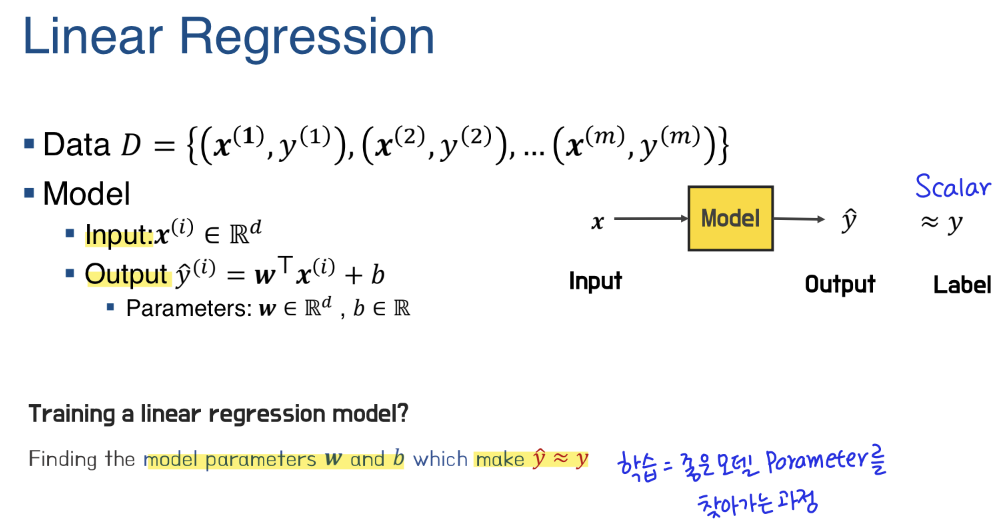
label과 하나 이상의 feature 사이의 선형 관계를 모델링 (가중치 W : x의 중요도)

Gradient Descent

Loss function과 Cost function이 위와 같다고 해보자!

Loss function: 하나의 데이터에 대한 실제값(y)과 예측값(y-hat)의 차이
Cost function: 전체 데이터의 오차, Loss function의 평균

우리의 목표는 Cost function J(W, b)를 minimize하는 모델 파라미터 W와 b를 찾는 것이다! 이를 위해서 이용하는 것이 Gradient Descent(경사 하강법)이다.

위 그림과 같이 미분값을 이용하여 (기울기가 양수일 때는 빼주고, 기울기가 음수일 때는 더해주는 방향으로!) cost function을 minimize 하는 model parameter를 찾아간다!

Learning rate: 하이퍼 파라미터(사용자가 지정해주는 파라미터)이다. 값이 크면 학습 속도는 빠를 수 있지만 발산할 가능성이 있고, 값이 작으면 학습이 느리게 진행될 수 있다!

Derivative with a Computation Graph

경사 하강법을 이용하기 위해 미분값을 구하는 과정을 살펴보자. 이 때 알고 있어야 할 개념은 Chain Rule 이다. Chain Rule을 이용할 때 아래와 같이 Computation Graph를 생각하면 도움이 된다!

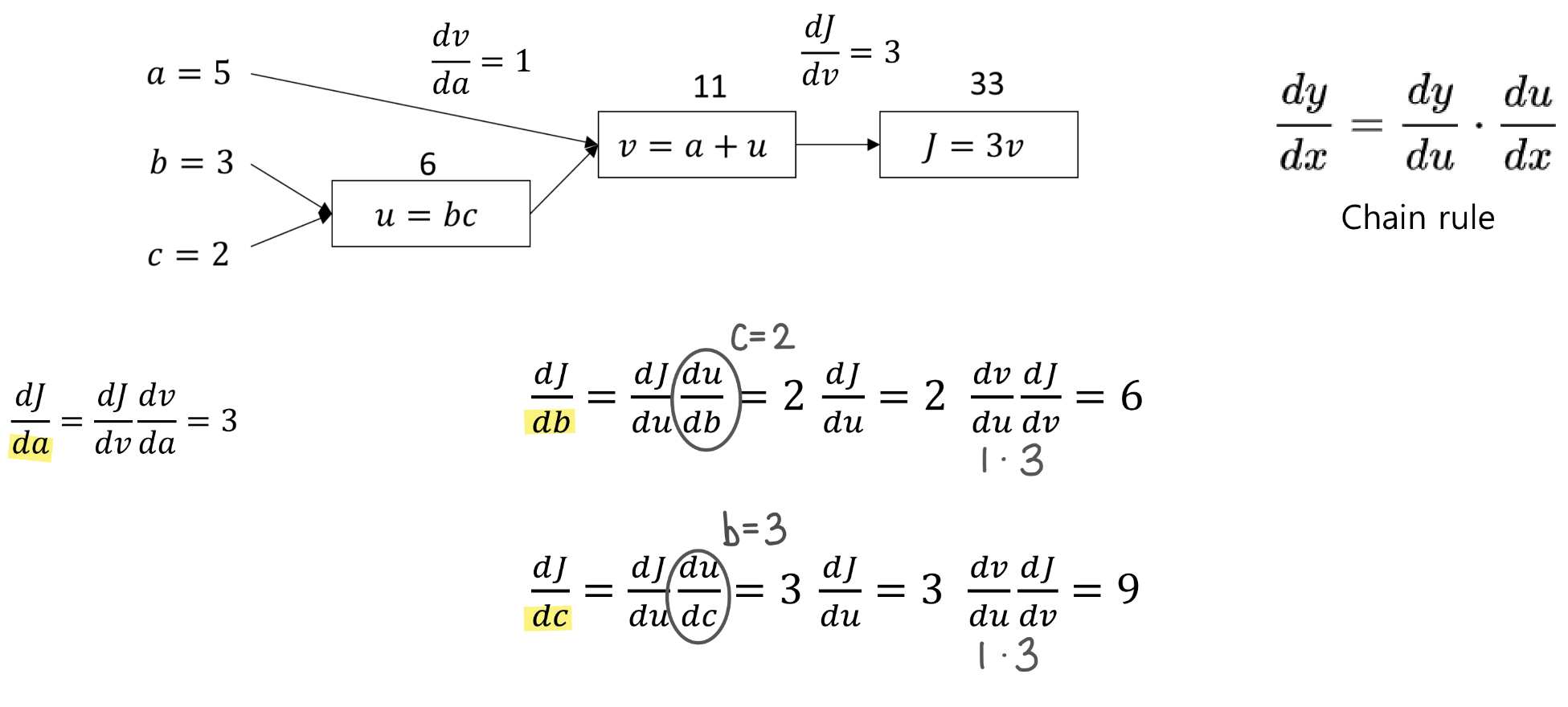
아래와 같이 Chain Rule을 이용하여 미분값을 구한 후, 역전파(backward propagation, 가중치 update)에 이용한다!

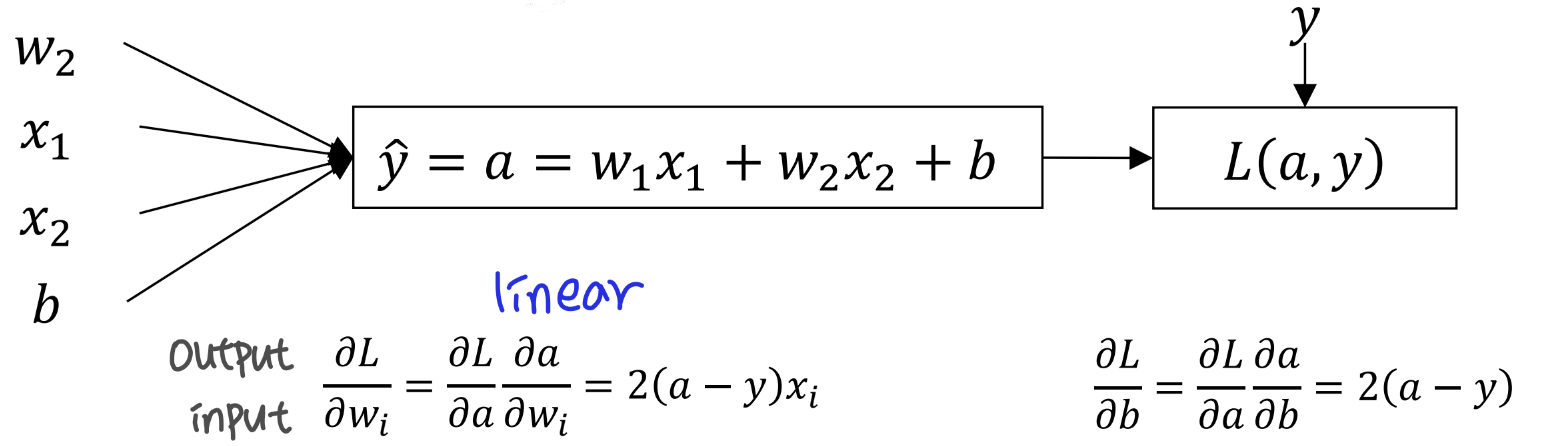
위 과정에서 이용한 Loss는 Squared Error : (y - yhat)^2 이다. 그래서 Cost function을 model parameter로 미분 값이 아래처럼 나오는 것이다.