백준 11657번: 타임머신

문제

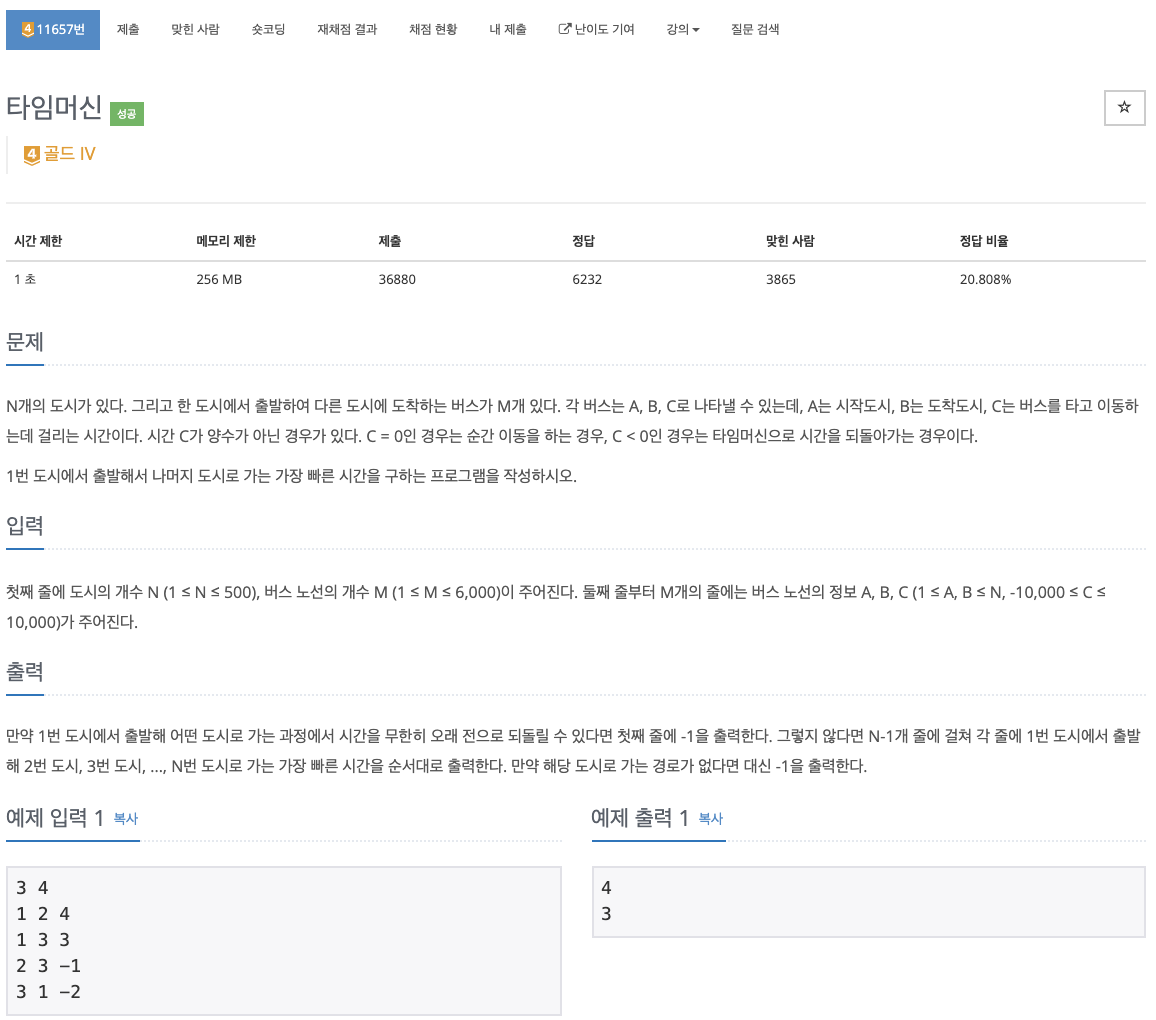문제 바로가기> 백준 11657번: 타임머신

풀이

Bellman-Ford 알고리즘을 이용하여 풀었다. 벨만-포드 알고리즘은 한 노드에서 다른 노드들까지의 최단거리를 구하는 알고리즘으로 다익스트라 알고리즘과 달리 간선의 가중치가 음수일 때도 사용이 가능하다. 하지만 다익스트라 알고리즘보다 속도가 느리므로 가중치가 모두 양수인 경우에는 다익스트라 알고리즘을 사용하는 것이 더 좋다.

#include<iostream>
#include<vector>
#define INF 2100000000
#define MAX_N 501
using namespace std;

int N, M;
bool cycle = false;
long long dist[MAX_N];
vector<pair<int, int> > graph[MAX_N];

int main(){
    ios_base::sync_with_stdio(0); cin.tie(0);
    cin >> N >> M;
    int a, b, c;
    for(int i=0; i<M; i++){
        cin >> a >> b >> c;
        graph[a].push_back(make_pair(b,c));
    }

    for(int i=2; i<=N; i++) dist[i] = INF; // 초기화
    dist[1] = 0; // 1번 정점에서 출발

    // 벨만-포드 알고리즘
    for(int i=1; i<=N; i++){ // 반복문을 N-1번 돌면 최단 거리 완성
        for(int j=1; j<=N; j++){
            for(int k=0; k<graph[j].size(); k++){
                int next_node = graph[j][k].first;
                int next_cost = graph[j][k].second;
                if(dist[j]!=INF && dist[j]+next_cost<dist[next_node]){ // 한번이라도 계산 된 정점인 경우
                    dist[next_node] = dist[j]+next_cost;
                    if(i==N) cycle = true; // 반복문을 한번 더 돌렸을 때 최단 거리 update = 음의 싸이클 존재
                }
            }
        }
    }
    if(cycle) cout << -1 << '\n'; // cycle이 있는 경우 (시간을 무한히 오래 전으로 되돌릴 수 있는 경우)
    else{
        for(int i=2; i<=N; i++){
            if(dist[i]==INF) cout << -1 << '\n'; // 해당 도시로 가는 경로가 없는 경우
            else cout << dist[i] << '\n'; // 해당 도시로 가는 최단 경로
        }
    }
}