백준 1238번: 파티

문제

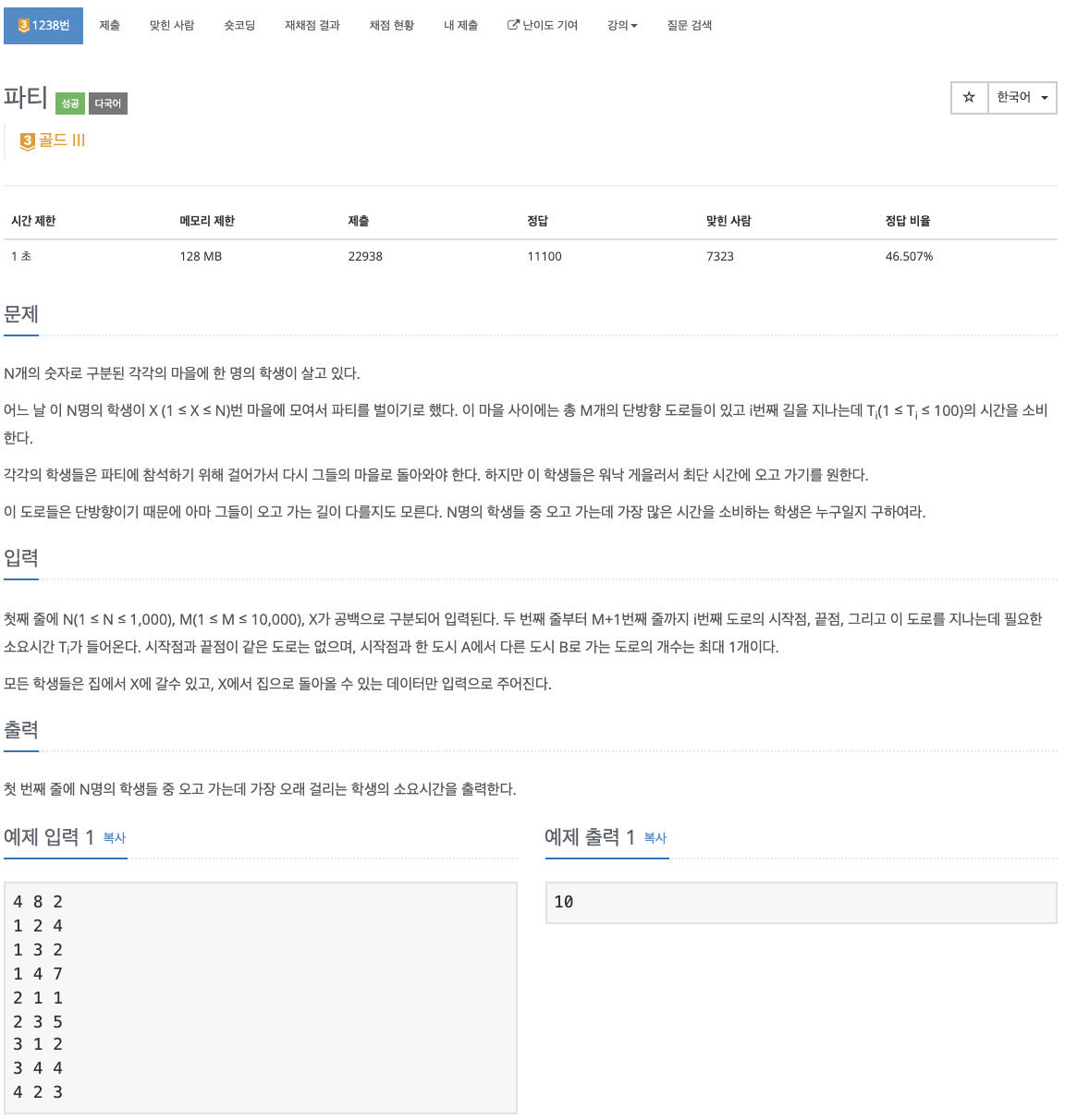문제 바로가기> 백준 1238번: 파티

풀이

다익스트라 알고리즘은 한 정점에서 다른 모든 정점으로 가는 최단 경로를 구해주는 알고리즘이다. 따라서 파티장소 X에서 집에 돌아갈 때는 쉽게 적용할 수 있지만, 다른 모든 정점에서 X로 가는 경우의 수는 어떻게 해야할까? 정답은 역방향 그래프를 만들어서 X를 출발점으로 생각하고 각 지점에 대한 최단 경로를 구해주면 된다.(도착 지점이 항상 X이므로, 이렇게 하면 원래 출발 지점에서 X로 가는 최단 경로와 일치한다.) 즉, 정방향 그래프와 역방향 그래프에 다익스트라 알고리리즘을 적용하여 빠른 시간 안에 문제를 해결할 수 있다. (이해가 잘 되지 않는다면 그림을 그려보면 쉽게 이해할 수 있다.)

#include<iostream>
#include<vector>
#include<queue>
#define INF 987654321
#define MAX_N 1001
#define MAS_M 10001
using namespace std;

struct Data{int end, time;}; // 도착 정점, 소요 시간
int N, M, X, s, e, t, dist1[MAX_N]={}, dist2[MAX_N]={};
vector<Data> graph[MAX_N], iv_graph[MAX_N];
bool visit[MAX_N];
void dijkstra(vector<Data> G[MAX_N]);

int main(){
    ios_base::sync_with_stdio(0); cin.tie(0);
    cin>>N>>M>>X;
    for(int i=0; i<M; i++){
        cin>>s>>e>>t;
        graph[s].push_back({e, t}); // 정방향 그래프
        iv_graph[e].push_back({s, t}); // 역방향 그래프
    }
    dijkstra(graph); // 정방향 그래프 다익스트라 알고리즘 수행
    dijkstra(iv_graph); // 역방향 그래프 다익스트라 알고리즘 수행
    int ans = 0; 
    for(int i=1; i<=N; i++) ans=max(ans, dist2[i]); // 최대 시간 찾기
    cout << ans;
}

void dijkstra(vector<Data> G[MAX_N]){
    for(int i=1; i<=N; i++) {
        dist1[i] = INF;
        visit[i] = false;
    }
    dist1[X]=0;
    priority_queue<pair<int, int> > pq;
    pq.push(make_pair(0, X));
    while (!pq.empty()){
        int curNode = pq.top().second; pq.pop();
        if(visit[curNode]) continue; // 이미 방문한 경우
        visit[curNode] = true;
        for(int i=0; i<G[curNode].size(); i++){
            int newTime = dist1[curNode]+G[curNode][i].time; // curNode를 거치는 경우
            int beforeTime = dist1[G[curNode][i].end]; // curNode를 거치지 않는 경우 
            if(newTime<beforeTime){ // 더 짧은 시간이 걸리는 경우 update 
                dist1[G[curNode][i].end] = newTime;
                pq.push(make_pair(-newTime, G[curNode][i].end));
            }
        }
    }
    for(int i=1; i<=N; i++) dist2[i]+=dist1[i];
}