Regular Expression to DFA

Converting a Regular Expression Directly to a DFA

• Algorithm 3.36 : Construction of a DFA from a regular expression $r$.
• INPUT : A regular expression $r$
• OUTPUT : A DFA $D$ that recognizes $L(r)$
• METHOD :
  1. augmented regular expression $(r)\#$으로부터 syntax tree $T$를 만들자.
  2. T에 대해 $nullable,\,firstpos,\,lastpos,\,followpos$를 앞에서의 방법을 이용해서 구하자.
  3. DFA $D$의 set of states인 $Dstates$와 $D$의 transition function인 $Dtran$을 아래 그림과 같은 방법으로 구하자.
     $D$의 states는 $T$의 position들의 set이다.
     $D$의 start state는 $n_0$가 $T$의 root node일 때, $firstpos(n_0)$에 해당한다.
     accepting states는 endmarker symbol $\#$을 포함하고 있는 position이다.
     

Minimizing the Number of States of a DFA

• 같은 Language를 가리키는 DFA라도 state의 수가 다를 수 있다.

  $Def.$ two automata are $the\,same\,up\,to\,state\,names$ if one can be transformed into the other by doing nothing more than changing the names of states.

• 각각의 상태들끼리는 close relationship이 존재한다.

• Fig. 3.36의 states $A$ 와 $C$는 사실상 동등한데, 둘 다 input $a$에 대해서는 $B$로 가고, input $b$에 대해서는 $C$로 간다.

• 또한, $A$와 $C$ 둘 다 Fig. 3.63.의 state 123과 동일하게 행동한다.

• 또, Fig. 3.36의 $B$는 Fig. 3.63의 state 1234와 동일하게, $D$는 1235와, $E$는 1236과 동일하게 행동한다.

• 그러므로, 어떤 regular language든 항상 unique한 minimum state를 가지는 DFA가 존재하고, 어떤 DFA든지 equivalent states끼리 묶는 것으로 만들 수 있다.

  $Def.$ string $x$ $distinguishes$ state $s$ from state $t$ if exactly one of the states reached from $s$ and $t$ by following the path with label $x$ is an accepting state.
  State $s$ is $distinguishable$ from state $t$ if there is some string that distinguishes them.

• ex) The empty string distinguishes any accepting state from any nonaccepting state.

• 또 뭔 소린지 모르겠다!!

• 정리하자면, states $s$, $t$가 있고, 만약 둘 다 string $x$를 통해서 진행시켰을 때, 둘 중 하나만 accepting state로 가는 경우에는 확실히 string $x$에 의해서 $s,t$가 regular expression을 만족하는지 아닌지 체크가 가능하다. 이런 맥락에서 $distinguish$ 한다고 하는 것 같음. (NFA 상에서도 유효한 정의인 것 같다.)

• state-minimization algorithm은 DFA를 distinguish되지 않는 상태끼리 그룹으로 묶어서 partition을 나누는 방법이다.

  • 알고리즘은 아직 서로 distinguish하지 않은 것들끼리 group으로 묶지만 서로 다른 group에 있는 state들 끼리는 모두 distinguishable 한 상태를 유지하면서 진행된다.
  • group들을 더 이상 쪼갤 수 없다면, minimum-state DFA를 얻은 것이다.
    

• 처음에 partition은 두 그룹으로 나누어진다 : accepting states와 nonaccepting states

  • fundamental step : 현재 partition의 몇 group을 선택한다, say $A=\{s_1,s_2,...,s_k\}$, and some input symbol $a$. 그리고 $a$가 group $A$의 states끼리 distinguish 할 수 있는지 살펴본다.
  • 즉, 각 $s_i$에 대해서 input $a$에 대한 transition을 다 시행해 보고, 서로 다른 state로 가는 것이 있으면 group을 나눈다.
  • 이 때, $s_i$와 $s_j$가 같은 state로 간다면 둘을 같은 그룹에 포함시킨다.
  • 이 과정을 그룹이 나누어지지 않을 때까지 반복한다.

• Algorithm 3.39 : Minimizing the number of states of a DFA

• INPUT : A DFA $D$ with set of states $S$, input alphabet $\Sigma$, start state $s_0$, and set of accepting states $F$.

• OUTPUT : A DFA $D'$ accepting the same language as D and having as few states as possible.

• METHOD :
  1. accepting state $F$, nonaccepting state $S-F$를 2개의 그룹으로 가진 initial partition $\Pi$로 시작한다.
  2. Fig. 3.64의 과정을 통해 새 파티션 $\Pi_{new}$를 만든다.
  
  3. 만약 $\Pi_{new}=\Pi$라면 let $\Pi_{final}=\Pi$, 그리고 step (4)로 간다. 만약 그렇지 않다면 step (2)로 가서 $\Pi_{new}$를 $\Pi$로 대체한다.
  4. 각 group에서 하나의 state를 그 group의 $representative$로 선택한다. 그 representatives는 minimum-state DFA $D'$의 states가 될 것이다. $D'$의 다른 요소들은 다음과 같이 만들어진다 :
  (a) $D'$의 start state는 $D$의 start state를 포함하고 있는 group의 representative이다.
  (b) $D'$의 accepting states는 $D$의 accepting state를 포함하고 있는 group들의 representatives이다. 참고로 처음에 accepting states와 nonaccepting states로 나누었고, 그것들을 내부적으로 나누었기 때문에 각각의 group들은 전부 다 accepting states 또는 전부 다 nonaccepting states로만 이루어져 있다.
  (c) $\Pi_{final}$의 어떤 그룹 $G$의 representative을 $s$, 그리고 $D$에서 state $s$에서 input $a$에서의 transition이 state $t$로 간다고 하자. $r$이 $t$의 group인 $H$의 representative라고 하자. 그러면 $D'$에서 input $a$에 대해 $s$에서 $r$로 가는 transition이 존재한다. -> 얘는 representative 끼리 transition을 가진다는 것을 보충설명하려고 한 것인듯.
  (Note that in $D$, every state in group $G$ must go to some state of group $H$ on input $a$, or else, group $G$ would have been split according to Fig. 3.64.)
  
  

State Minimization in Lexical Analyzers

• Fig. 3.54의 경우 initial partition은
  $\{0137,7\}\{247\}\{8,58\}\{68\}\{\emptyset\}$이다.
• 앞에서 봤을 때에는 accepting state라고 하나로 퉁쳐서 말했지만, 사실 같은 accepting state라도 다른 token을 생성하는 것이라면 다른 accepting state로 생각해야 할 것 같다. 위의 예시에서도 그렇게 하는걸.
• Dead state를 표시하기는 했지만 transition이 없는 것을 dead state로의 transition이라고 생각해도 좋다.

Trading Time for Space in DFA Simulation

• 가장 간단하고 빠른 방법
  • DFA의 transition function을 2차원 table로 만들기.
  • 단점 : DFA의 states가 너무 많고 ASCII만 해도 128개니까 너무 많은 메모리 차지.
• 개선 방법
  transition table 대신에 각각의 state마다 character-state pair를 만들어 놓고, 가장 많은 input에 대해서는 else 처리를 해 놓아서 메모리를 적게 쓰게 한다.
  Fig. 3.66에서의 방법
  $base$ array는 state $s$를 위한 $next$, $check$ array에 있는 entry들의 base location을 결정하기 위해 쓰인다.
  $default$ array는 $check$ array에 의해 $base[s]$가 invalid하다고 결정났을 경우, alternative base location을 찾기 위해 쓰인다.
  
  
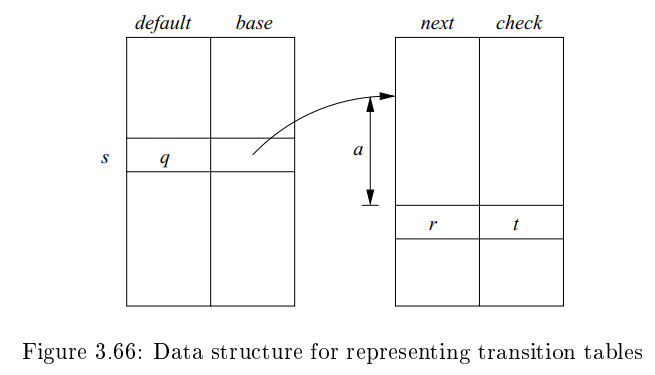
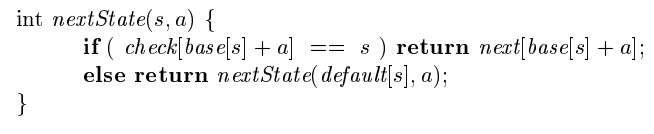
  여기는 대충 넘어가도 될듯.