Optimization of DFA-Based Pattern Matchers

• regular expression 으로부터 만들어진 pattern matchers를 optimize 해보자.
• 3 가지의 알고리즘이 있다.

  1. regular expression으로 부터 NFA를 거치지 않고 바로 DFA를 만들어낸다. DFA의 states 수도 기존의 NFA를 통해서 DFA를 만들었을 때 보다 적게 가진다. -> useful in a Lex compiler
  2. 같은 양상을 보이는 states들을 합침으로써 DFA의 states의 수를 최소화 한다. 이 알고리즘은 $O(n\,logn)$의 시간복잡도를 가진다. (n : DFA의 states의 수)
  3. 기존의 2차원 transition table이 아닌, 더 compact한 transition table을 만든다.

Important States of an NFA

• regular expression을 DFA로 바꾸기 전에, NFA를 만드는 알고리즘 3.23에서 여러 states들의 역할을 분석해 봐야 한다.
• state of an NFA important if it has a non-$\epsilon$ out-transition. (중의적이다.. 그러니까 $\epsilon$이 아닌 다른 transition이 존재하는 state를 의미한다. 모든 transition이 $\epsilon$이 아닌 것이 아니라..) 그냥 내가 잘 못 해석한 듯.
• 즉, set of states $move(s, a)$가 nonempty라면 state $s$는 important하다.
• subset construction에서 NFA states의 두 sets는 아래의 조건을 만족하면 identify될 수 있다.
  1. Have the same important states
  2. Either both have accepting states or neither does.
• Algorithm 3.23의 방법에서, important states는 basis part에서의 initial states밖에 없다.
• 즉, 각각의 important state는 regular expression에서의 particular operand에 해당한다.
• 완성된 NFA는 오직 하나의 accepting state를 가지고 있지만, 이 state는 out-transition을 갖지 않기 때문에 not-important하다.
• regular expression$r$ 뒤에 unique한 endmarker인 $\#$을 붙임으로써 accepting state 또한 $(r)\#$에 대해 important한 state로 만들 수 있다.
• 그 후에 위 과정을 적용하면 되고, $\#$에 대한 transition이 있는 상태는 accepting state일 것이다.

Functions Computed From the Syntax Tree

• regular expression -> DFA를 바로 얻기 위해서 syntax tree를 만들고 4개의 function을 계산해야 한다.

  1. $nullable(n)$ is true for a syntax-tree node n if and only if the subexpression represented by $n$ has $\epsilon$ in its language.
     즉, subexpression은 "made null"이나 empty string이 될 수 있다.
  2. $firstpos(n)$ is the set of positions in the subtree rooted at $n$ that correspond to the first symbol of at least one string in the language of the subexpression rooted at $n$.
  3. $lastpos(n)$ is the set of positions in the subtree rooted at n that correspond to the last symbol of at least one string in the language of the subexpression rooted at $n$.
  4. $followpos(p)$, for a position $p$, is the set of positions $q$ in the entire syntax tree such that there is some string $x=a_1a_2...a_n$ in $L((r)\#)$ such that for some i, there is a way to explain the membership of $x$ in $L((r)\#)$ by matching $a_i$ to position $p$ of the syntax tree and $a_{i+1}$ to position$q$.

• 뭔 소린지 모르겠다!!
• 예시를 통해서 봅시다.
• 일단 여기서 말하는 node는 operator 부분, position은 operand 부분을 말하는 듯.
  
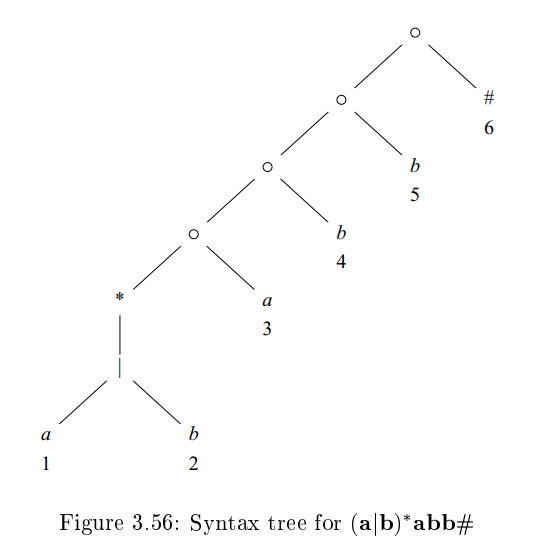
• expression $(a|b)^*a$의 cat node를 $n$번째 node라고 해봅시다.
  • 그러면 $nullable(n)$은 false인데, 그 이유는 cat node에 의해서 만들어지는 expression들은 항상 마지막이 $a$로 끝나기 때문에 $\epsilon$을 만들지 않는다.
  • 반대로 $*$ node는 $\epsilon$을 만들 수 있으므로 $nullable(n^*)$는 true이다.
  • $firstpos(n)=\{1, 2, 3\}$이다.
    • node n에 의해서 만들어진 문자열 중 예를 들어
    • $aa$의 경우 첫 번째 $a$는 position 1로부터 만들어진 것이고, $ba$의 경우 첫 번째 $b$는 position 2로부터 만들어진 것이다.
    • $a$의 경우 position 3으로부터 만들어진 것이다.
  • $lastpos(n)=\{3\}$이다.
    • node n에 의해서 만들어진 어떤 문자열이건 간에 항상 $a$로 끝나므로 position 3으로부터 만들어질 수 밖에 없다.
  • $followpos$는 만들기 복잡하다. 예시를 통해 알아보자.
    • $followpos(1)=\{1, 2, 3\}$이 된다.
    • string $...ac...$를 생각해 보자. (c는 a 또는 b, a는 position 1에 해당함)
    • 그렇다면 $a$는 $*$의 마지막 부분일 수도 있고, 아닐 수도 있다.
    • 마지막인 경우, 그 다음에 처음으로 나오는 position은 3 일 수 밖에 없다.
    • 마지막이 아닌 경우, 그 다음에 나올 수 있는 position은 1 또는 2 밖에 없다.
    • 그러므로 1, 2, 3이 $followpos(1)$이 된다.
• 다시 정리해 봅시다. ㄹㅇ 4줄 요약.

  1. node n의 subtree가 $\epsilon$이 표현 가능 -> true, else -> false
  2. node n의 subtree에서 첫 번째 위치에 올 수 있는 녀석들.
  3. node n의 subtree에서 마지막 위치에 올 수 있는 녀석들.
  4. position p 다음에 올 수 있는 녀석들.

Computing $nullable,\,firstpos,$ and $lastpos$

• straightforward recursion으로 $nullable,\,firstpos,\,lastpos$를 구할 수 있다.
  
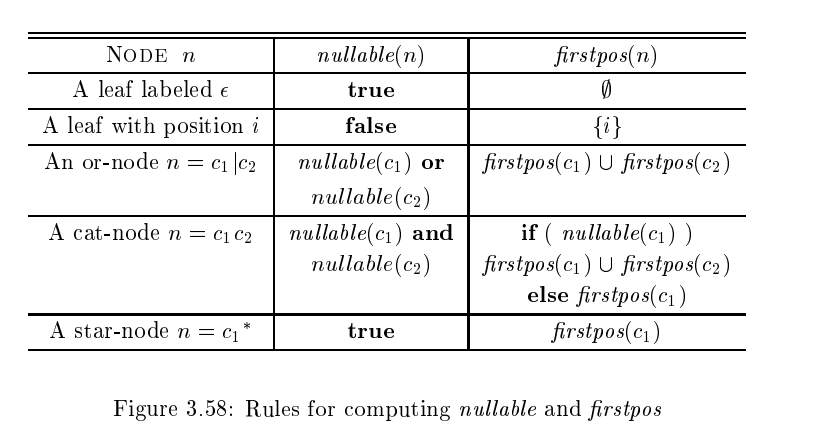
• $lastpos(n)$의 경우에는 $firstpos(n)$과 거의 유사하다.

Computing $followpos$

1. 만약 $n$이 left child $c_1$, right child $c_2$를 갖는 cat-node라면, $lastpos(c_1)$에 있는 모든 position i에 대해서 $firstpos(c_2)$의 모든 position들은 $followpos(i)$에 속해 있다.
2. 만약 $n$이 star-node이고 $i\in lastpos(n)$이라면, $firstpos(n)$의 모든 position들은 $followpos(i)$에 속한다.

• 개인적인 생각으로는 $followpos$ 자체가 뒤에 이어지는 것을 찾는 건데 이것은 cat 연산하고 $*$ 연산만 가능하기 때문에 이 두 연산에 대해서만 정의를 하는 듯.
• $followpos$함수를 방향 그래프를 통해서 표현할 수 있다. (아래 그림 참고)
  
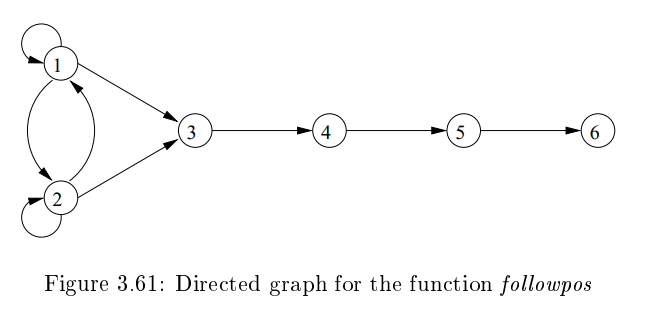
• NFA와 형태는 거의 비슷한데, 아래의 작업을 하면 NFA가 될 수 있다.
  1. root의 $firstpos$에 있는 모든 position들을 initial state로 만든다.
  2. $i$에서 $j$로 가는 각 arc에 대해서 position $i$의 symbol을 써 넣는다.
  3. endmarker $\#$과 연결된 position만 accepting state로 만든다.