📔설명
데이터 마이닝을 알아보자!
데이터 마이닝
: 기존 통계와 달리 대용량 데이터베이스 시스템에서 데이터들간의 의미있는 패턴을 파악하거나 예측하여 의사결정에 활용
CRM의 발전으로 성장
데이터 마이닝 방법론
-
목적- 문제
예측 - 결과
해석
- 문제
-
종류- 분류분석
- 예측분석
- 군집분석
- 연관성분석
데이터 마이닝 절차
SAS에서 사용하고 있는SEMMA 방법SPSS, 테라데이타, 다임러, NCR등에서 개발한CRISP-DM
🧂데이터 마이닝의 개요
데이터 마이닝
대용량 데이터에서의미있는 패턴을파악하거나예측하여의사결정에 활용하는 방법
통계분석과의 차이점
통계분석:가설이나가정에 따른 분석이나 검증데이터 마이닝: 다양한 수리 알고리즘을 이용해데이터베이스의데이터로부터의미있는 정보를찾아내는 방법
종류
| 정보를 찾는 방법론에 따른 종류 | 분석대상, 활용목적, 표현방법에 따른 분류 |
|---|---|
| -인공지능(Artificial Intelligence) -의사결정나무(Decision Tree) -K-평균 군집(K-means Clustering) -연관분석(Association Rule) -회귀분석(Regression) -로짓분석(Logit Analysis) -최근접이웃법(k-Nearest Neighbor) | -시각화분석(Visualization Analysis) -분류(Classification) -군집화(Clustering) -예측(Forecasting) |
사용분야
- 병원에서 환자 데이터를 이용해 해당 환자에게 발생 가능성이 높은 병
예측 기존 환자가 응급실에 왔을 때 어떤 조치를 먼저 해야 하는지 결정고객 데이터를 이용해 해당 고객의우량/불량을예측해 대출적격 여부 판단- 세관 검사에서
입국자의 이력과 데이터를 이용해 관세물품 반입 여부예측
데이터 마이닝의 최근 환경
데이터 마이닝 도구가다양하고체계화되어환경에 적합한제품을 선택해 활용 가능알고리즘에 대한 깊은 이해가 없어도분석에 큰 어려움X분석 결과의품질은분석가의 경험과역량에 따라 차이가 나므로분석 과제의 복잡성이나중요도가 높으면전문가에게의뢰국내에서 데이터 마이닝이 적용된 시기는1990년대 중반2000년대에비즈니스 관점에서 데이터 마이닝이CRM의 중요한 요소로 부각- 대중화를 위해 많은 시도가 있었으나,
통계학 전문가와대기업위주로 진행
데이터 마이닝의 분석 방법
| Supervised Learning(지도학습) | Unsupervised Learning(비지도학습) |
|---|---|
| -의사결정나무(Decision Tree) -인공신경망(Artificial Neural Network, ANN) -일반화 선형 모형(Generalized Linear Model, GLM) -선형 회귀분석(Linear Regression Analysis) -로지스틱 회귀분석(Logistic Regression Analysis) -사례기반 추론(Case-Based Reasoning) -최근접 이웃(k-Nearest Neighbor,kNN) | -OLAP(On-Line Analytical Processing) -연관성 규칙(Association Rule Discovery, Market Basket) -군집분석(k-Means Clustering) -SOM(Self Organizing Map) |
분석 목적에 따른 작업 유형과 기법
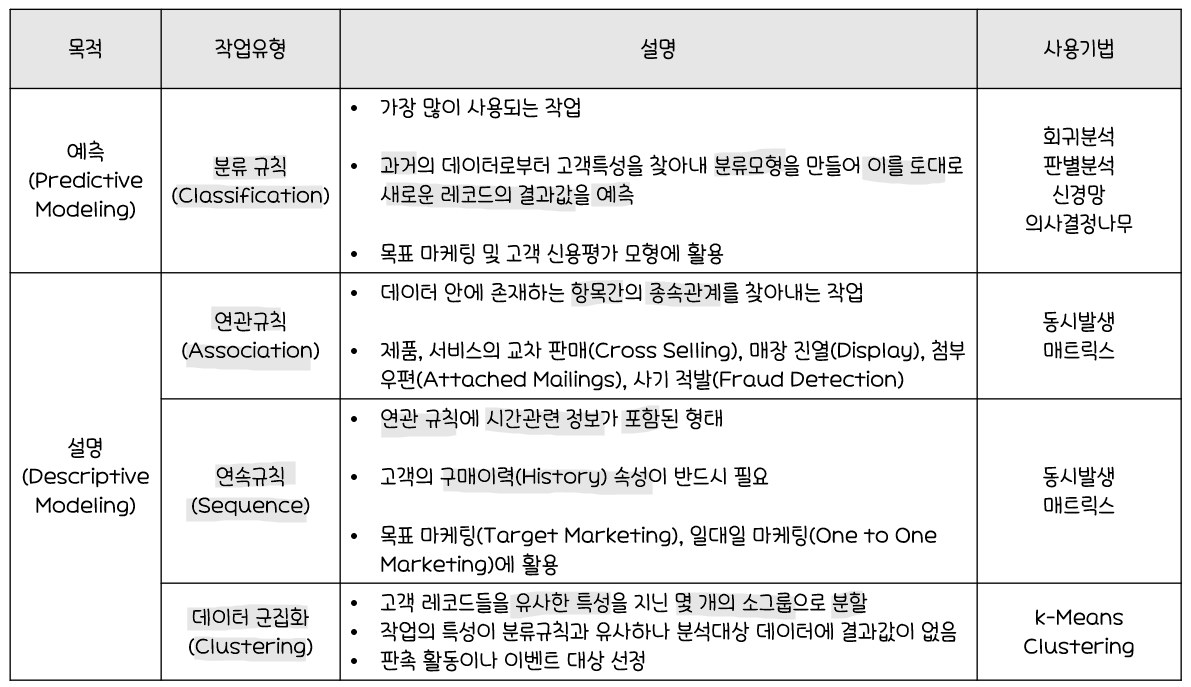
*판별분석(Discriminant Anlysis)
: 두 개 이상의 모집단에서 추출된 표본들이 지니고 있는 정보를 이용해 이 표본들이 어느 모집단에서 추출된 것인지를 결정해줄 수 있는 기준을 찾는 분석
데이터 마이닝 추진단계
1단계 : 목적 설정
데이터 마이닝을 통해무엇을왜하는지명확한 목적(이해관계자 모두 동의하고 이해할 수 있는)설정전문가가 참여해목적에 따라 사용할모델과필요 데이터정의
2단계 : 데이터 준비
- 고객정보, 거래정보, 상품 마스터정보, 웹로그 데이터, 소셜 네트워크 데이터 등
다양한 데이터활용 IT부서와 사전에 협의하고 일정을 조율해데이터 접근 부하에 유의- 필요시 다른 서버에 저장하여
운영에 지장이 없도록데이터 준비 데이터 정제를 통해 데이터의품질을 보장하고, 필요시 데이터를보강하여충분한 양의데이터 확보
3단계 : 가공
모델링 목적에 따라목적 변수(y)정의- 필요한
데이터를데이터 마이닝 소프트웨어에 적용할 수 있는 형식으로가공
4단계 : 기법 적용
1단계에서명확한 목적에 맞게데이터 마이닝 기법을 적용하여정보 추출
5단계 : 검증
- 데이터 마이닝으로 추출된
정보 검증 테스트 데이터와과거 데이터를 활용해최적의 모델선정검증이 완료되면IT부서와 협의해상시 데이터 마이닝 결과를업무에 적용하고,보고서를 작성하여추가 수익과투자대비성과(ROI)등으로기대효과전파
데이터 마이닝을 위한 데이터 분할
- 모델 평가용
테스트 데이터와구축용 데이터로 분할하여,구축용 데이터로모형 생성,테스트 데이터로 모형이 얼마나적합한지 판단
데이터 분할
구축용(Training Data, 50%)
추정용,훈련용 데이터데이터 마이닝 모델을만드는 데 활용
검정용(Validation Data, 30%)
- 구축된 모형의
과대추정또는과소추정을미세 조정하는데 활용
시험용(Test Data, 20%)
테스트 데이터나과거 데이터를 활용해모델의 성능을 검증
데이터의 양이 충분하지 않은 경우
-
홀드아웃(Hold-Out) 방법
: 주어진 데이터를랜덤하게두 개의 데이터로 구분하여 사용하는 방법
-학습용(Training Data)와시험용(Test Data)로 분리하여 사용 -
k-fold 교차분석(Cross-Validation) 방법
: 주어진 데이터를k개의 하부 집단으로 구분하여,k-1개의 집단을학습용,
나머지는하부집단으로검증용으로 설정하여 학습
-k번 반복 측정한 결과를평균낸 값을최종값으로 사용.
-주로10-fold 교차분석사용
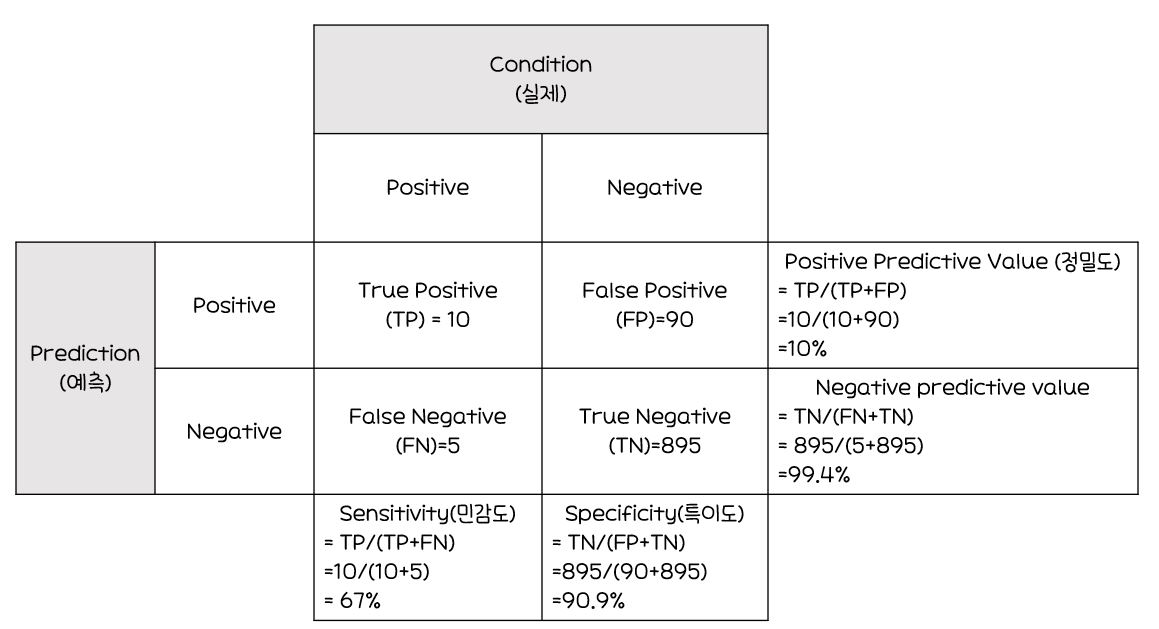
성과분석
오분류에 대한 추정치
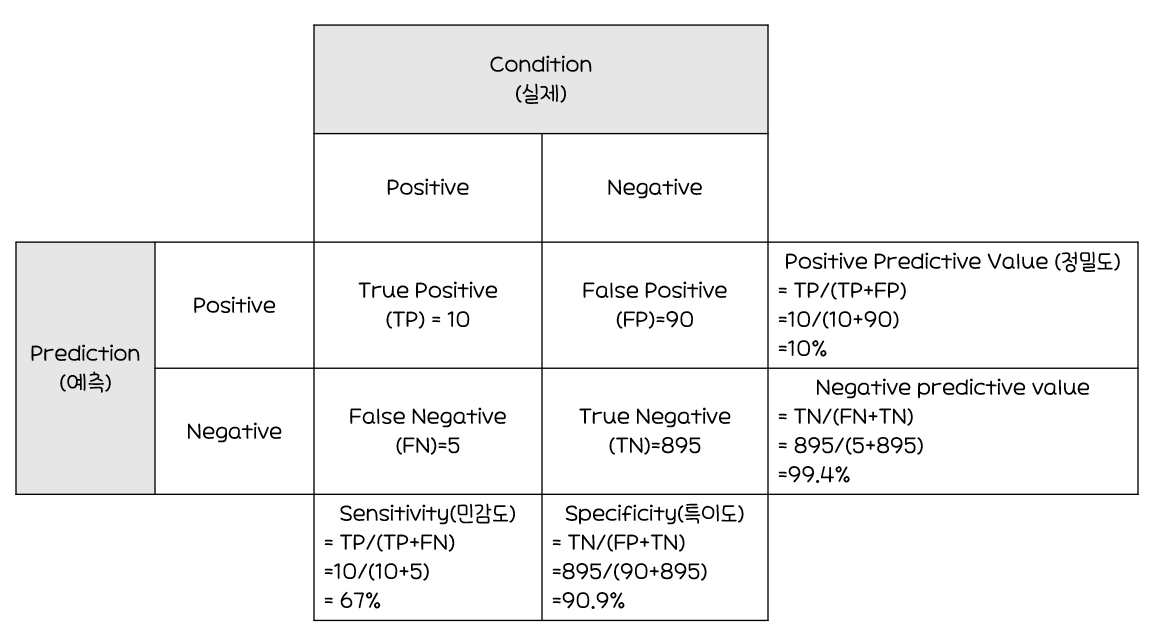
-
정분류율(Accuracy)
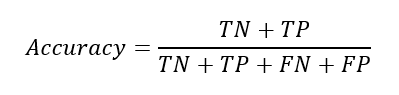
-
오분류율(Error Rate)
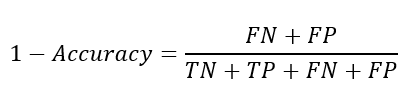
-
특이도(Specificity)
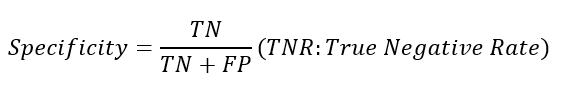
-
민감도(Sensitivity)
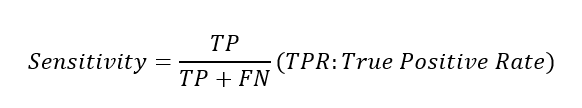
-
정밀도(Precision)
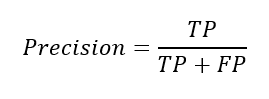
-
재현율(Recall)=민감도
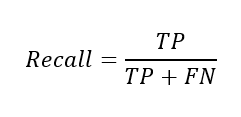
-
F1 Score
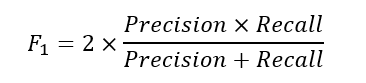
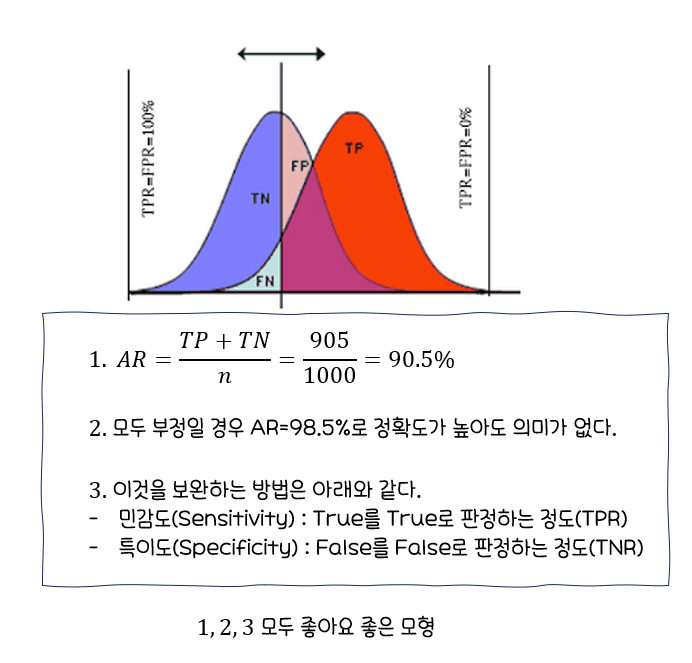
*코헨 카파 상관계수(Cohen's Kappa Coefficient)
: 모델의 예측값과 실제값의 일치여부를 판정하는 통계량
0~1사이의 범위를 가지며,1에 가까울수록예측-실제값일치
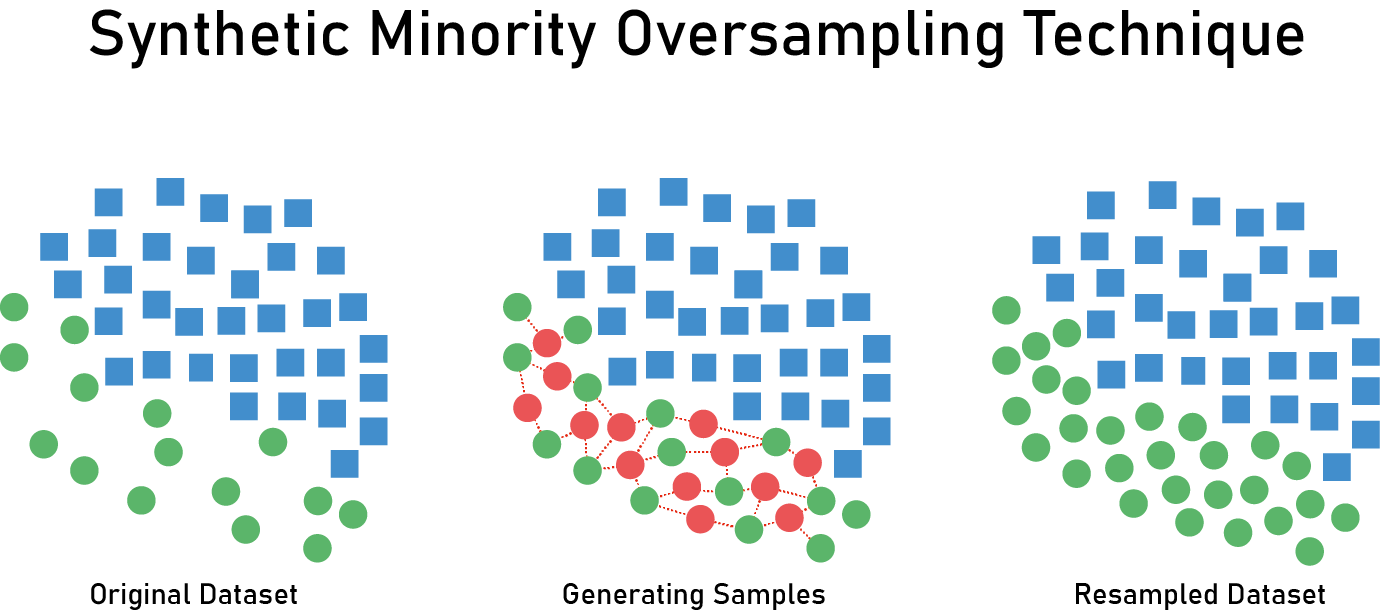
*클래스 불균형(Class Imbalance)
: 분류할 각 집단에 속하는 데이터 수가 동일하지 않은 경우
오버 샘플링또는언더 샘플링등의 해결 방안으로 처리
ROCR 패키지로 성과분석
ROC Curve(Receiver Operating Characteristic Curve)
ROC Curve:가로축을FPR(Ralse Positive Rate, 1-특이도),
세로축을TPR(True Positive Rate, 민감도)로 두어시각화한그래프2진 분류(Binary Classfication)-추론값과 정답값이 (참, 거짓) 2개인 것에서 모형의성능을평가하기 위해 사용되는 척도
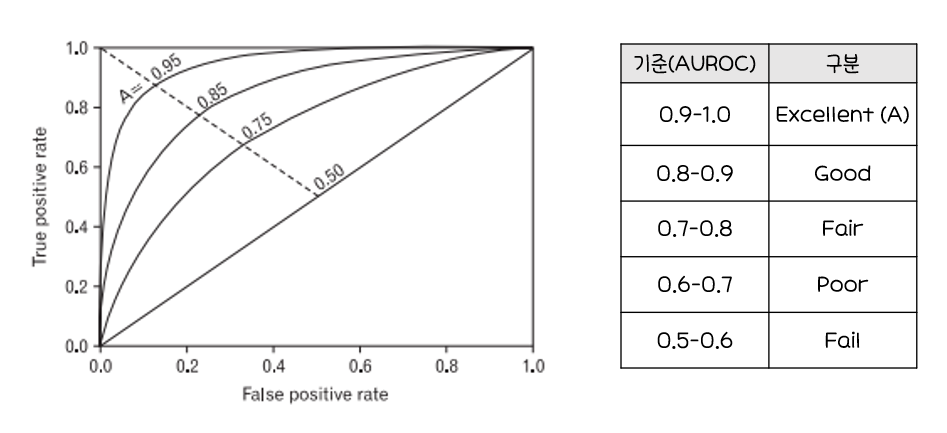
- 그래프가
왼쪽 상단에가깝게그려질 수록올바르게 예측한 비율은높고,잘못 예측한 비율은낮음 AUROC(Area Unser ROC,ROC곡선 아래의 면적)값이크면 클수록(1에 가까울 수록)모형의성능이좋음TPR(True Positive Rate, 민감도):1인 케이스에 대한1로 예측한 비율FPR(False Positive Rate, 1-특이도):0인 케이스에 대한1로 잘못 예측한 비율
ROC Curve와AUROC의활용예시
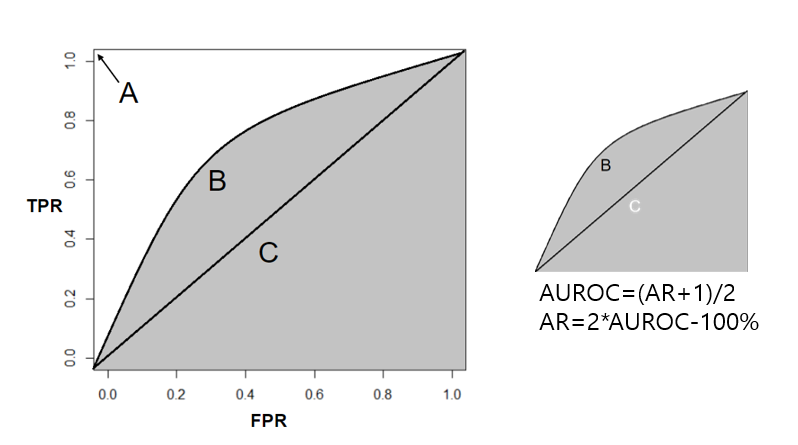
R실습
ROCR 패키지는Binary Classification만 지원
library(rpart)
library(party) #의사결정나무분석 포함된 패키지
library(ROCR)
#척추후만증 데이터를 nrow(kyphosis) 사이즈만큼 sample()로 무작위 추출
# replace=F로 한 번 추출한 값은 제외
x<-kyphosis[sample(1:nrow(kyphosis),nrow(kyphosis),replace=F),]
#sample()로 뽑힌 무작위 데이터 중 75%는 학습용 데이터
x.train<-kyphosis[1:floor(nrow(x)*0.75),]
#학습용 데이터 뒤부터 끝까지 평가용 (25%)
x.evaluate<-kyphosis[floor(nrow(x)*0.75):nrow(x),]
#cforest : 조건 랜덤포레스트
x.model<-cforest(Kyphosis~Age+Number+Start, data=x.train)
#x.evaluate에 없던 것을 추가. 예측
x.evaluate$prediction<-predict(x.model, newdata=x.evaluate)
x.evaluate$correct<-x.evaluate$prediction==x.evaluate$Kyphosis
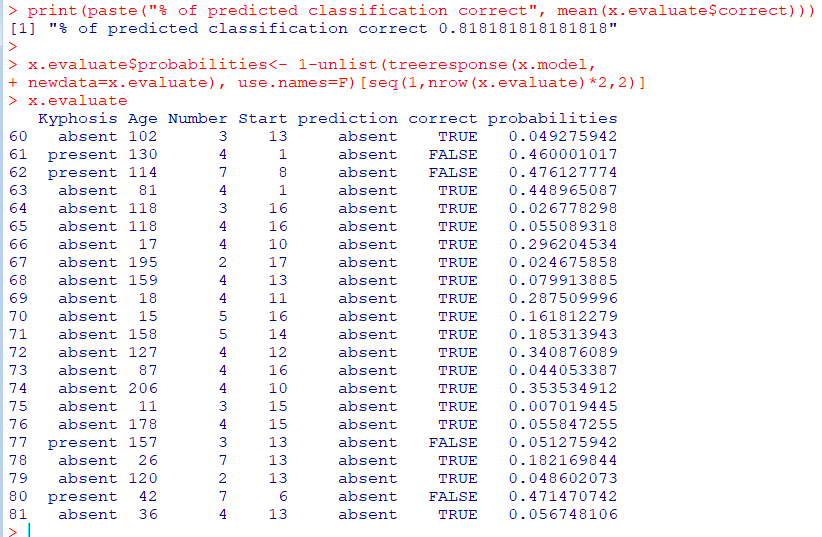
print(paste("% of predicted classification correct", mean(x.evaluate$correct)))
#treeresponse는 list로 되므로 unlist 사용, probabilities는 확률
x.evaluate$probabilities<- 1-unlist(treeresponse(x.model,
newdata=x.evaluate), use.names=F)[seq(1,nrow(x.evaluate)*2,2)]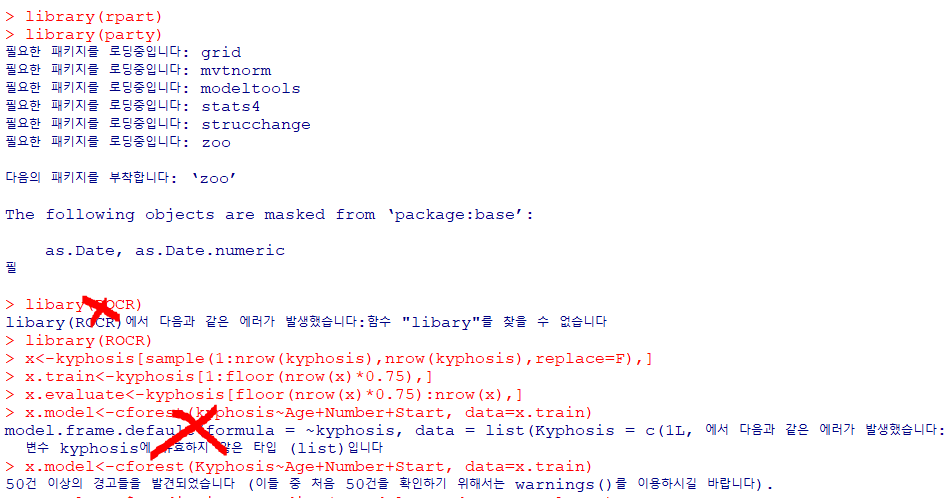
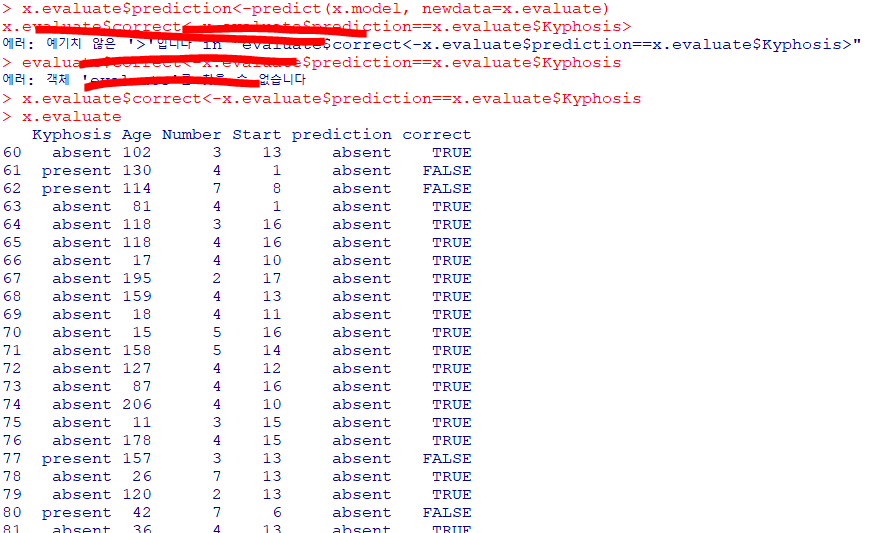
그래프1
#prediction(예측, 레이블(실제값))
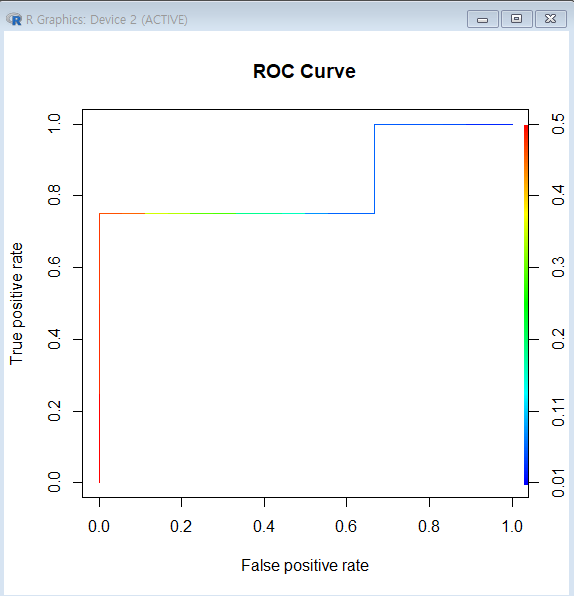
pred<-prediction(x.evaluate$probabilities,x.evaluate$Kyphosis)
#ROC Curve를 그리기 위한 민감도, 1-특이도 계산
perf<-performance(pred, "tpr","fpr")
plot(perf, main="ROC Curve", colorize=T)
그래프2
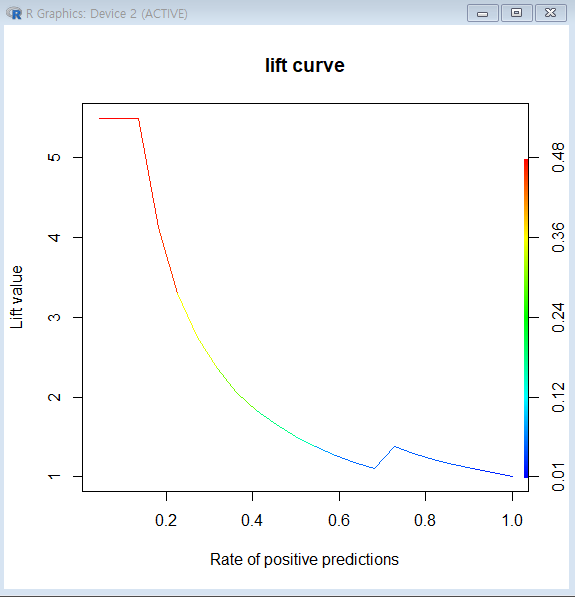
# ROC 커브가 아닌 lift Curve//향상도 곡선
perf<-performance(pred,"lift","rpp")
#랜덤 모델과 비교했을 때, 해당 모델의 성과가 얼마나 향상됐는지 각 등급별로 파악
plot(perf, main="lift curve", colorize=T)
*sample()
: 벡터혹은 데이터 프레임에서 지정된 크기만큼 데이터를 무작위로 추출할 때 사용하는 R 함수
*set.seed()
: 난수를 생성하고 다시 난수를 생성하면 다른 결과가 나온다.
이전과 동일한 난수를 생성하고 싶을 때 사용해 지정 가능
이익도표(Lift chart
이익도표의개념
분류모형의성능을평가하기 위한 척도분류된 관측치에 대해 얼마나예측이 잘 이루어졌는지를 나타내기 위해임의로 나눈 각 등급별로반응검출율,반응률,리프트등의 정보를 산출하여 나타내는 도표2000명의 전체고객중381명이상품을 구매한 경우에 대해이익도표를 만드는 과정을 예로 살펴보자.- 먼저,
데이터셋의 각관측치에 대한예측확률을내림차순으로 정렬. - 이후 데이터를
10개의 구간으로 나눈 다음 각 구간의반응율(% response)산출 기본 향상도(Baseline Lift)에 비해반응률이몇 배나 높은지를 계산 (향상도(Lift))
- 먼저,
이익도표의 각등급은예측확률에 따라매겨진 순위이므로,상위 등급에서더 높은 반응률을 보이는 것이좋은 모형
이익도표의활용 예시
- 전체 2000명 중 381명이 구매
기본 향상도(Baseline Lift)= 구매자/전체 = 381/2000Frequency of "buy": 2000명 중실제 구매자% Captured Response:반응검출율=해당 등급 실구매자/전체 구매자% response:반응률=해당 등급의 실구매자/200명(2000/10)Lift:향상도=반응률/기본향상도, 좋은 모델이라면Lift가 빠른 속도로 감소해야 함등급별로향상도가 급격하게변동할수록좋은 모형각 등급별로향상도가 들쭉날쭉하면좋은 모형 X
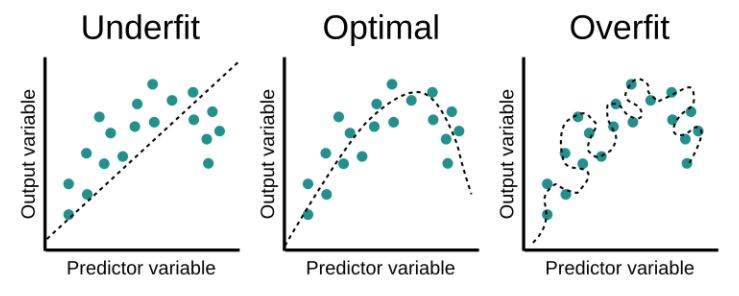
*과대적합(과적합), 과소적합의 개념
-
과적합/과대적합(Overfitting): 모형이학습용 데이터를 과하게 학습하여,학습 데이터에 대해서는높은 정확도를 나타내지만,테스트 데이터혹은 다른 데이터에 적용할 때는성능이 떨어지는 현상 -
과소적합(Underfitting): 모형이 너무단순하여 데이터 속에 내제되어있는패턴이나규칙을제대로 학습하지 못한 경우.지나친 일반화
*Bias-Variance Trade-Off
: 모델을 학습시킬 때 Bias(편향)과 Variance(분산)이 최소화가 되도록 해야지만, 하나가 커지면 하나가 작아지고 하나가 작아지면 하나가 커지기 때문에 서로 Trade-Off 관계
🎩분류분석
분류분석과 예측분석
분류분석의 정의
- 데이터가
어떤 그룹에 속하는지예측하는데 사용되는 기법 클러스터링과유사하나분류분석은각 그룹이정의되어있음교사학습(Supervised Learning)에 해당하는 예측기법
예측분석의 정의
시계열분석처럼시간에 따른값두 개만을 이용해앞으로의 매출또는온도등을 예측모델링을 하는입력 데이터가 어떤 것인지에 따라특성이 다름여러 개의 다양한설명변수(독립변수, X)가 아닌,한 개의 설명변수(X)
분류분석, 예측분석의 공통점과 차이점
공통점
- 레코드의
특정 속성의값을미리 알아맞히는 점
차이점
분류: 레코드의범주형 속성의 값을 알아맞힘예측: 레코드의연속형 속성의 값을 알아맞힘
분류, 예측의 예
분류
- 학생들의 국어, 영어, 수학 점수를 통해
내신등급을 알아맞힘 - 카드회사에서 회원들의 가입정보를 통해
1년 후 신용등급을 알아맞힘
예측
- 학생들의 여러 가지 정보를 입력해
수능 점수를 알아맞힘 - 카드회사 회원들의 가입정보를 통해
연 매출액을 알아맞힘
분류 모델링
- 신용평가모형(우량/불량)
- 사기방지모형(사기/정상)
- 이탈모형(이탈/유지)
- 고객세분화(VVIP/VIP/GOLD/SILVER/BRONZE)
분류 기법
- 로지스틱 회귀분석
- 의사결정나무
- CART
- 나이브 베이즈 분류
- 인공신경망
- 서포터 벡터 머신(SVM)
- k 최근접 이웃(kNN)
- 규칙기반의 분류와 사례기반 추론(Case-Based Reasoning)
로지스틱 회귀분석(Logistic Regression)
반응변수(y)가범주형인 경우에 적용되는회귀분석모형- 새로운
설명변수(예측변수, X)가 주어질 때반응변수의 각범주(or 집단)에 속할확률이 얼마인지를추정(예측모형)하여,추정 확률을 기준치에 따라분류하는 목적(분류모형)으로 활용 사후확률(Posterior Probability): 모형의적합을 통해추정된 확률
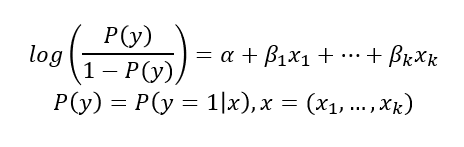
exp(β_1): 나머지변수(x_1, ..., x_k)가 주어질 때,x_1이한 단위 증가할 때마다성공(Y=1)의오즈가몇 배 증가하는지를 나타내는 값
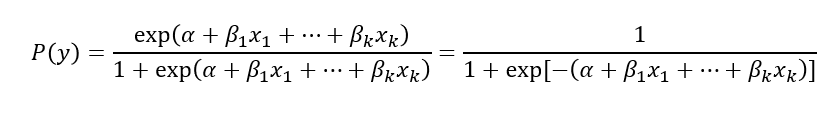
- 위는
다중로지스틱 회귀모형 - 그래프의 형태 :
설명변수가한 개(x1)인 경우 해당회귀계수 β1의부호에 따라S자 모양(β1>0)또는역 S자 모양(β1<0) 표준 로지스틱 분포의누적분포함수 F(x)
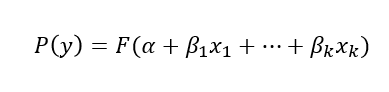
- 위 식과 동일한 표현이며,
표준 로지스틱 분포의누적분포함수로성공확률추정
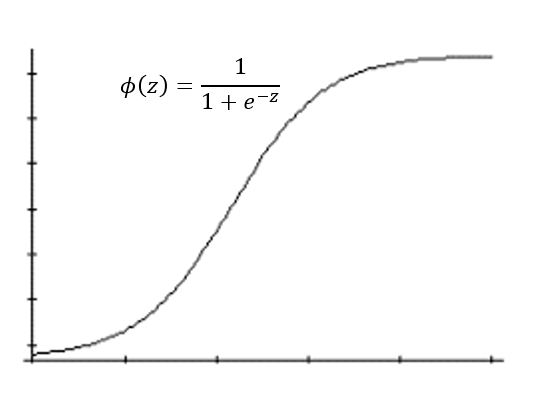
선형회귀분석과로지스틱 회귀분석의비교
glm()함수를 이용해로지스틱 회귀분석실행
#family=binomial은 로지스틱 회귀분석시 이항식으로
glm(종속변수~독립변수1 + ...+ 독립변수k, family=binomial, data=데이터셋명)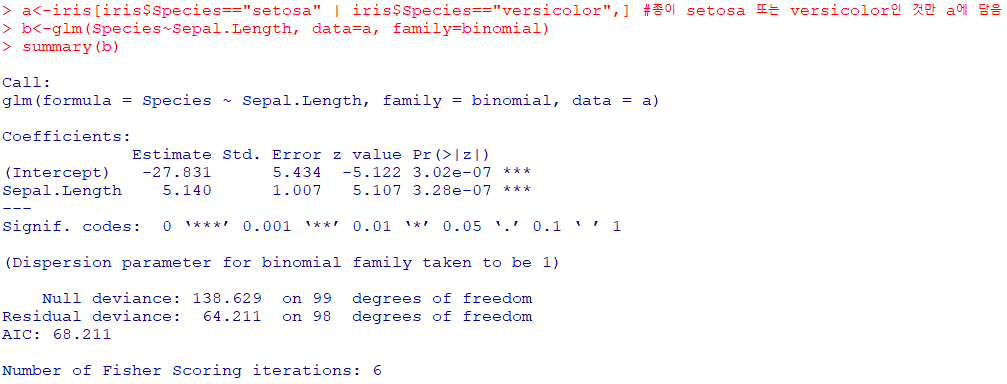
-
종속변수: Species,독립변수: Sepal.Length -
Sepal.Length가한 단위 증가함에 따라Species(Y)가
1에서 2로 바뀔 때오즈(Odds)가 exp(5.140)≈170배 (β가 음수이면 감소) -
Null deviance
:절편만 포함하는 모형의완전 모형으로부터의이탈도(Deviance)
=> p-값=P(𝜒^2(99)>138.629)≈0.005으로통계적으로 유의하므로 적합결여 -
Residual deviance
:예측변수 Sepal.Length가추가된 적합 모형의이탈도
=>Null deviance에 비해자유도 1기준이탈도의 감소가74.4정도 큰 감소
=> p-값=P(𝜒^2(98)>64.211)≈0.997으로통계적으로 유의하지 못해귀무가설 기각 X -
적합값이 관측된 자료를 잘적합함
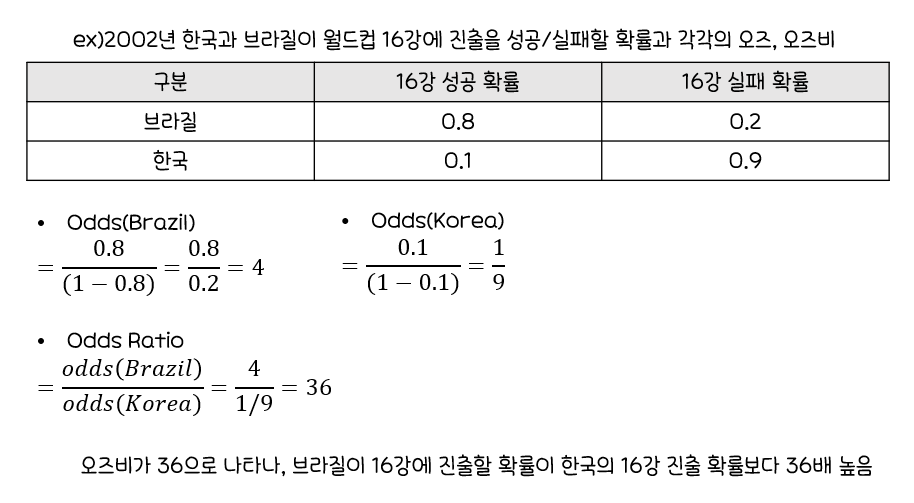
*오즈와 오즈비
오즈(Odds):성공할 확률이실패할 확률의몇 배인지를 나타내는확률오즈비(Odds Ratio): 두 오즈의비율
의사결정나무
정의
의사결정나무:분류함수를의사결정 규칙으로 이뤄진나무 모양으로 그리는 방법나무구조는 연속적으로 발생하는의사결정 문제를시각화해의사결정이 이뤄지는시점과성과를 한눈에 볼 수 있음계산 결과가 의사결정나무에 직접 나타나므로해석 간편- 주어진
입력값에 대하여출력값을예측하는 모형 분류나무모형회귀나무모형
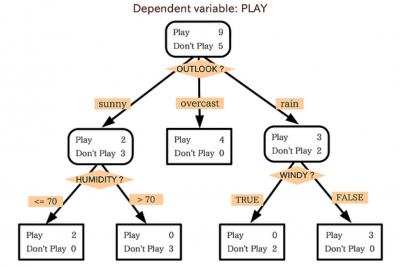
*의사결정나무의 구성요소
뿌리마디(Root Node): 시작되는 마디. 전체자료 포함자식마디(Child Node): 하나의 마디로부터 분리되어 나간 2개 이상의 마디들부모마디(Parent Node): 주어진 마디의 상위 마디끝마디(Terminal Node): 자식마디가 없는 마디중간마디(Internal Node): 부모마디와 자식마디가 모두 있는 마디가지(Branch): 뿌리마디로부터 끝마디까지 연결된 마디들깊이(Depth): 뿌리마디부터 끝마디까지의 중간마디들의 수
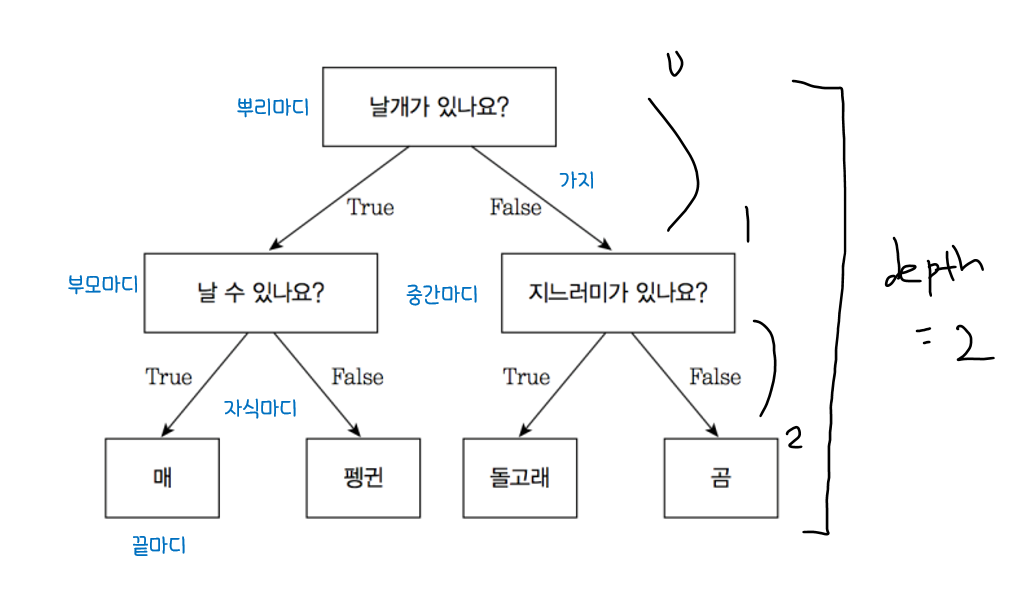
예측력과 해석력
- 기대집단의 사람들 중 가장 많은 반응을 보일
고객의유치방안을예측하고자 하는 경우에는예측력에 치중 - 신용평가에서는 심사 결과 부적격 판정이 나온 경우 고객에게
부적격 이유를설명해야하므로해석력에 치중
의사결정나무의 활용
-
세분화
: 데이터를비슷한 특성을 갖는 몇 개의그룹으로분할해 그룹별특성을 발견하는 것 -
분류
: 여러예측변수들에 근거해 관측개체의목표변수 범주를몇 개의 등급으로분류하고자 하는 경우에 사용 -
예측
: 자료에서규칙을 찾아내고 이를 이용해미래의 사건을 예측하고자 하는 경우 -
차원축소및변수선택
:매우 많은 수의예측변수중에서목표변수에 큰 영향을 미치는변수들을 골라내고자 하는 경우에 사용 -
교호작용효과의파악
: 여러 개의예측변수들을결합해목표변수에 작용하는규칙을파악하고자 하는 경우
범주의 병합또는연속형 변수의이산화:범주형 목표변수(y)의범주를 소수의 몇 개로 병합하거나,연속형 목표변수(y)를몇 개의 등급으로이산화하고자 하는 경우
의사결정나무의 특징
장점
결과를 누구에게나설명하기용이- 모형을 만드는 방법이
계산적으로 복잡X 대용량 데이터에서도빠르게만들 수 있음비정상 잡음 데이터에 대해서도민감함 없이 분류 가능한 변수와상관성이 높은다른 불필요한 변수가 있어도크게 영향X설명변수나목표변수에수치형변수와범주형변수모두 사용 가능모형 분류 정확도가높음
단점
새로운 자료에 대한과대적합발생 가능성 높음분류 경계선 부근의자료값에 대해서오차 큼설명변수 간의중요도를 판단하기 쉽지 않음
의사결정나무의 분석과정(형성과정)
성장 단계
: 각마디에서 적절한최적의 분리규칙(Splitting Rule)을 찾아내나무를 성장시키는 과정
- 적절한
정지규칙(Stopping Rule)만족시중단
가지치기 단계
:오차를크게 할 위험이 높거나부적절한 추론규칙을 가지고 있는가지또는불필요한 가지를제거
타당성 평가 단계
:이익도표(Gain Chart),위험도표(Risk Chart)혹은시험자료를 이용해의사결정나무를평가
해석및예측 단계
: 구축된 나무모형을해석하고예측모형을 설정한 후예측에적용하는 단계
나무의 성장
훈련자료를(xi, yi) i=1,2,...,n으로 나타낸다.
여기서,xi=(xi1,...,xip)- 나무모형의 성장과정은
x들로 이루어진입력 공간을재귀적으로 분할하는 과정
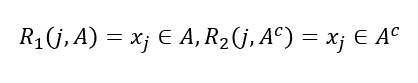
분리규칙(Splitting Rule)
분리 변수(Split Variable)가연속형인 경우

분리변수가범주형{1, 2, 3, 4}인 경우
:A=1,2,4와A^c=3으로 나뉨최적 분할의 결정은불순도 감소량을 가장크게하는 분할
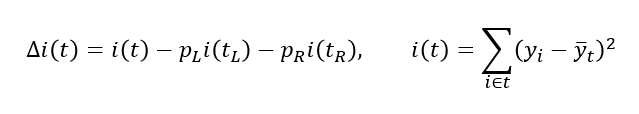
각 단계에서최적 분리기준에 의한분할을 찾은 다음각 분할에 대하여도동일한 과정 반복
분리기준(Splitting Criterion)
이산형 목표변수
| 기준값 | 분리기준 |
|---|---|
| 카이제곱 통계량 p값 | P값이 가장 작은 예측변수와, 그 때의 최적분리에 의해서 자식마디를 형성 |
| 지니 지수 | 지니 지수를 감소시켜주는 예측변수와, 그 때의 최적분리에 의해서 자식마디 선택 |
| 엔트로피 지수 | 엔트로피 지수가 가장 작은 예측 변수와, 이 때의 최적분리에 의해 자식마디 형성 |
정지규칙(Stopping Rule)
- 더 이상
분리가 일어나지 않고, 현재의 마디가끝마디가 되도록 하는 규칙 정지기준(Stopping Criterion): 의사결정나무의깊이(Depth)를 지정,끝마디의레코드 수의최소 개수를 지정
나무의 가지치기(Pruning)
너무 큰 나무모형은 자료를과대적합하고,너무 작은 나무모형은과소적합할 위험 존재나무의 크기를 모형의복잡도로 보며,최적의 나무 크기는자료로 부터 추정- 일반적으로
마디에 속하는 자료가일정 수(ex.5)이하일 때,분할을 정지하고비용-복잡도 가지치기(Cost Complexity Runing)을 이용해 성장시킨 나무를가지치기함
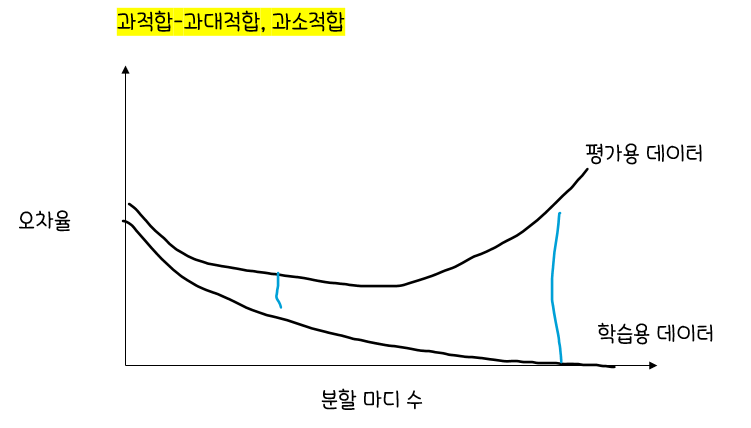
불순도의 여러 가지 측도
목표변수(y)가범주형변수인의사결정나무의 분류규칙을 선택하기 위해서 카이제곱 통계량, 지니지수, 엔트로피 지수 활용
카이제곱 통계량
: 각셀에 대한((실제도수-기대도수)의 제곱/기대도수)의 합
기대도수=열의 합계x합의 합계/전체합계
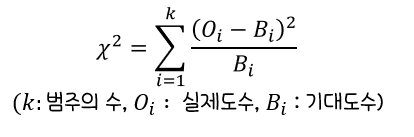
지니지수
:노드의불순도를 나타내는 값
지니지수 값이클수록이질적(Diversity)이며순수도(Purity)가낮다
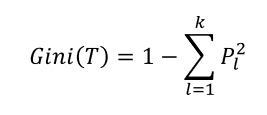
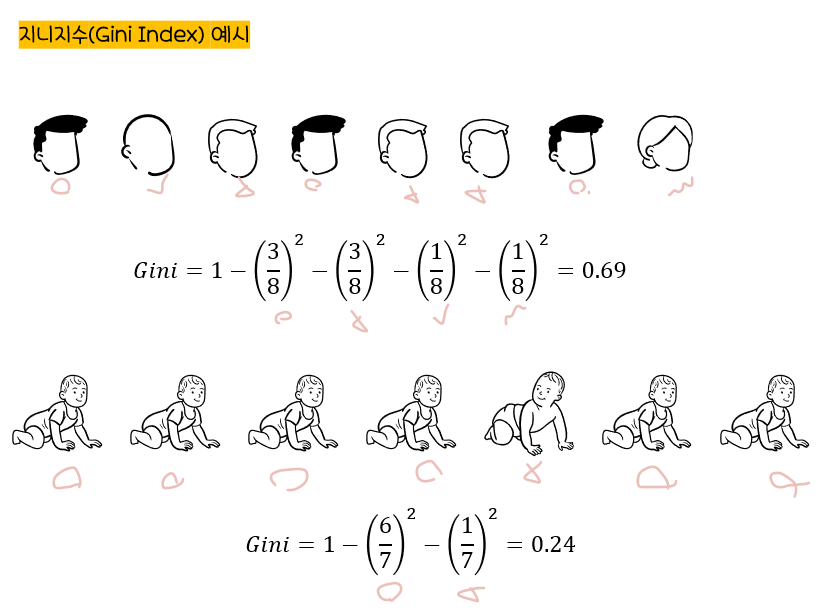
엔트로피 지수
:열역학에서 쓰는 개념으로무질서 정도에 대한 측도
엔트로피 지수의 값이클수록순수도(Purity)가낮다엔트로피 지수가가장 작은예측 변수와 이때의최적분리 규칙에 의해자식마디 형성
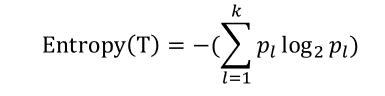

의사결정나무 알고리즘
CART(Classification and Regression Tree)
- 앞에서 설명한 방식의 가장 많이 활용되는
의사결정나무 알고리즘 불순도의 측도로출력(목적)변수가범주형일 경우 :지니지수연속형인 경우 :분산을 이용한이진분리(Binary Split)사용개별 입력변수뿐만 아니라입력변수들의 선형결합들 중에서최적의 분리를 찾을 수 있음
C4.5와 C5.0
CART와 다르게각 마디에서다지분리(Multiple Split)이 가능범주형 입력변수에 대해서는범주의 수만큼분리가 일어남불순도의 측도:엔트로피 지수
CHAID(CHi-Squared Automathic Interaction Detection)
가지치기를하지 않고적당한 크기에서 나무모형의성장을 중지입력변수가 반드시범주형 변수불순도의 측도:카이제곱 통계량
의사결정나무 예시
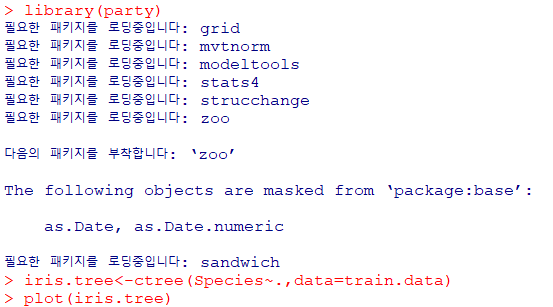
party 패키지를 이용한 의사결정나무
party 패키지:의사결정나무를 사용하기 편한 다양한 분류 패키지 중 하나분실값을 잘처리하지 못하는 문제를 갖고 있는 단점tree에 투입된데이터가표시되지 않거나predict가실패하는 경우 문제 발생
iris data를 이용한 분석
iris data: 30%는 test data, 70%는 training data
#prob : 랜덤 추출 확률 지정, 1이 선택될 확률 0.7, 2가 선택될 확률 0.3
#2 : 1 또는 2
idx<-sample(2,nrow(iris),replace=TRUE,prob=c(0.7,0.3))
train.data<-iris[idx==1,]
test.data<-iris[idx==2,]
train.data를 이용하여모형 생성
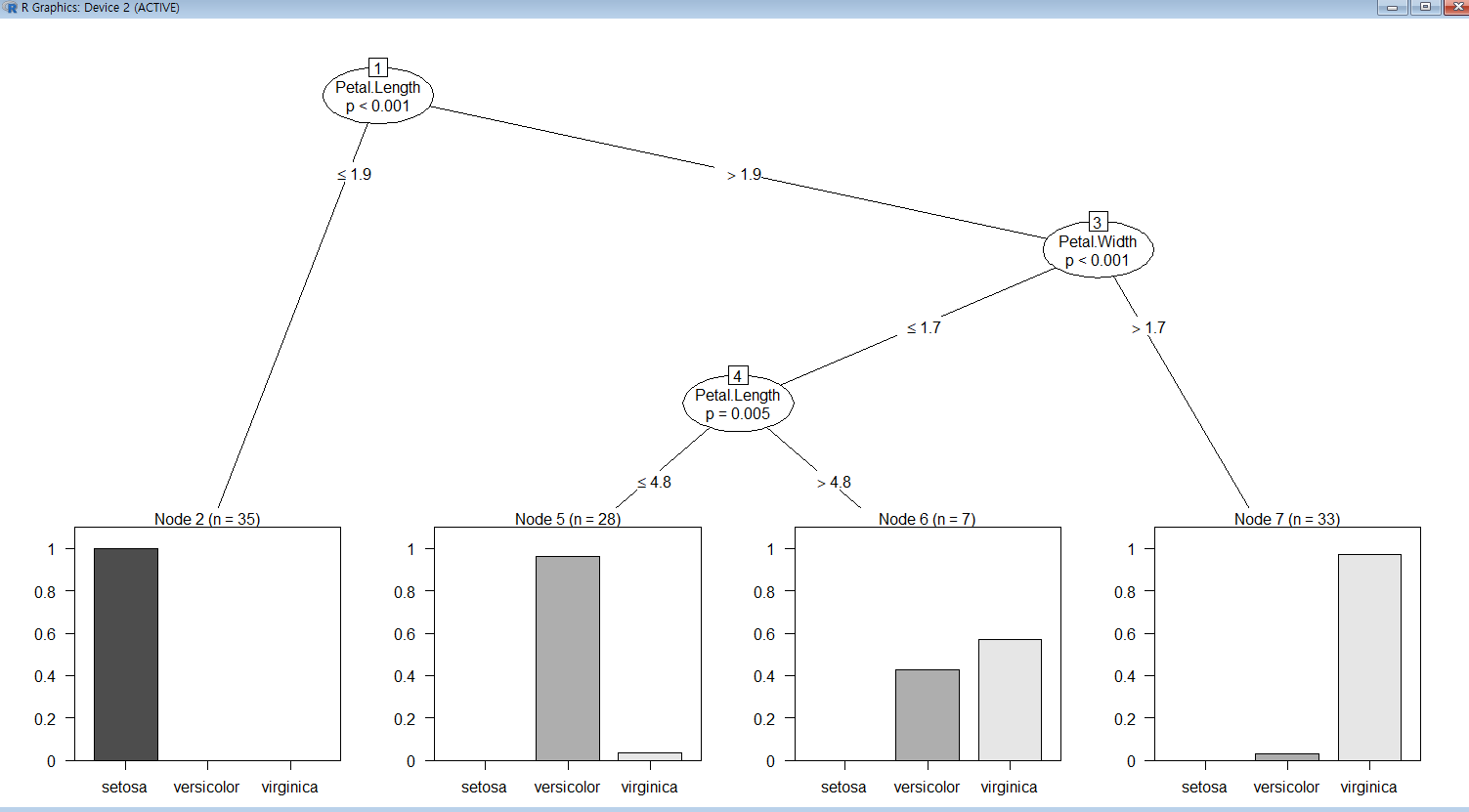

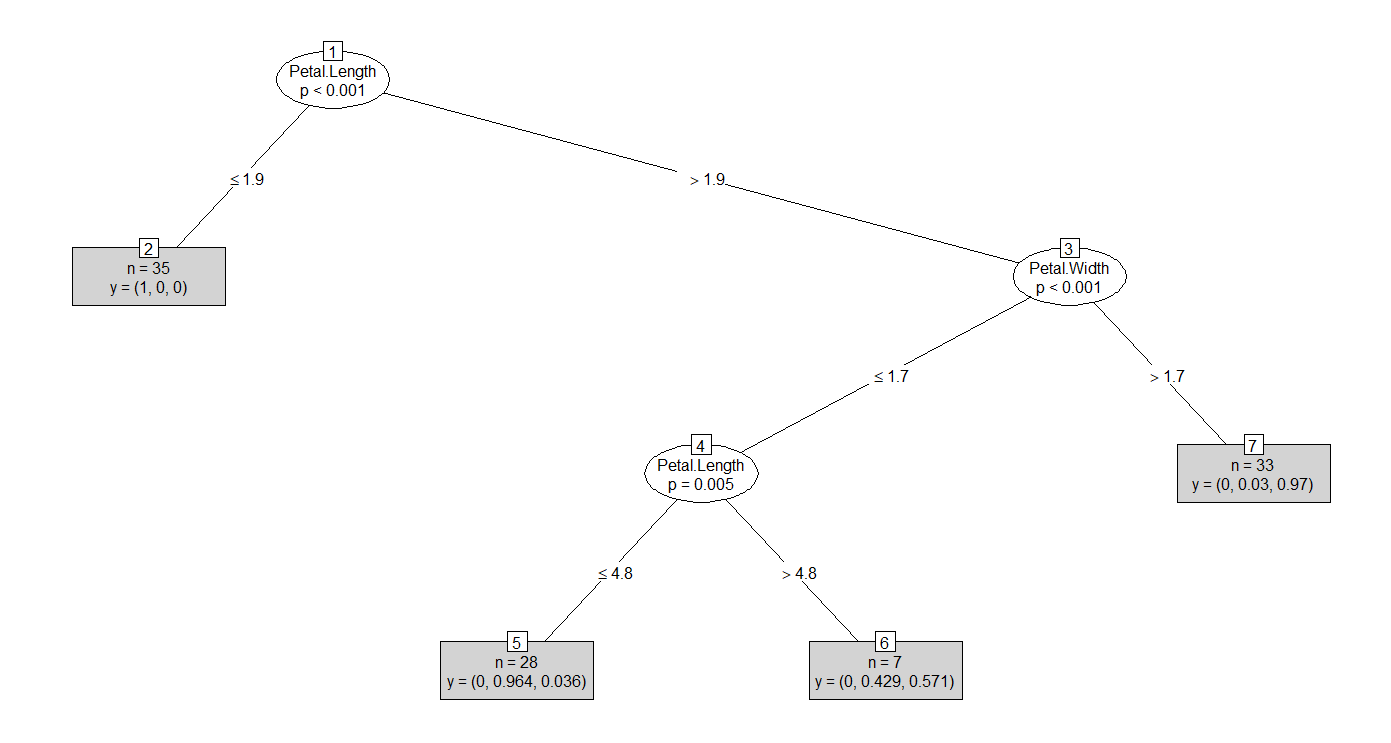
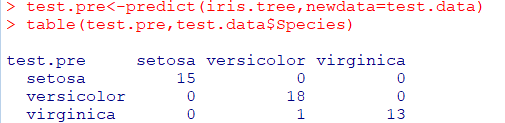
예측된 데이터와실제 데이터비교

test data를 적용하여정확성 확인
🎹앙상블 분석
앙상블(Ensemble)
주어진 자료로부터여러 개의예측모형들을 만든 후예측모형들을조합하여하나의 최종 예측 모형을 만드는 방법다중 모델 조합(Combining Multiple Models),분류기 조합(Classifier Combination)이 있음
학습방법의 불안전성
학습자료의작은 변화에 의해예측모형이크게 변하는 경우, 그 학습방법은불안정가장 안정적인 방법:1-Nearest Neighbor(가장 가까운 자료만 변하지 않으면 예측 모형이 변하지않음),선형회귀모형(최소제곱법으로 추정해 모형 결정)이 존재가장 불안정한 방법:의사결정나무
앙상블 기법의 종류
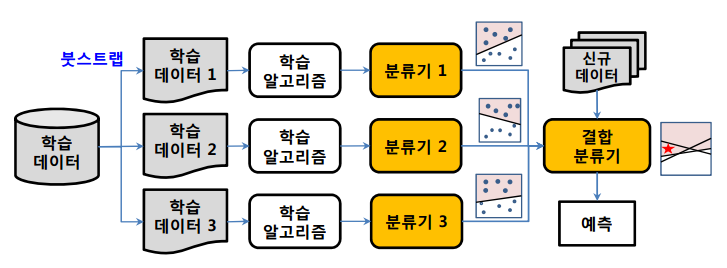
배깅
Breiman(1994)에 의해 제안- 주어진 자료에서
여러 개의붓스트랩(Bootstrap)자료를생성하고, 각 붓스트랩 자료에예측모형을 만든 후결합하여최종 예측모형을 만드는 방법 붓스트랩
: 주어진 자료에서동일한 크기의표본을랜덤 복원추출로뽑은 자료보팅(Voting):여러 개의 모형으로부터 산출된 결과를다수결에 의해서최종 결과를선정최적의 의사결정나무를 구축할 때 가장 어려운 부분이가지치기이지만,
배깅에서는가지치기를하지 않고최대로 성장한 의사결정나무활용훈련자료의 모집단의 분포를모르기때문에 실제 문제에서는평균예측모형을 구할 수 없음.
=>배깅은 이러한 문제를 해결하기 위해훈련자료를모집단으로 생각하고평균예측모형을 구해분산을 줄이고 예측력 향상
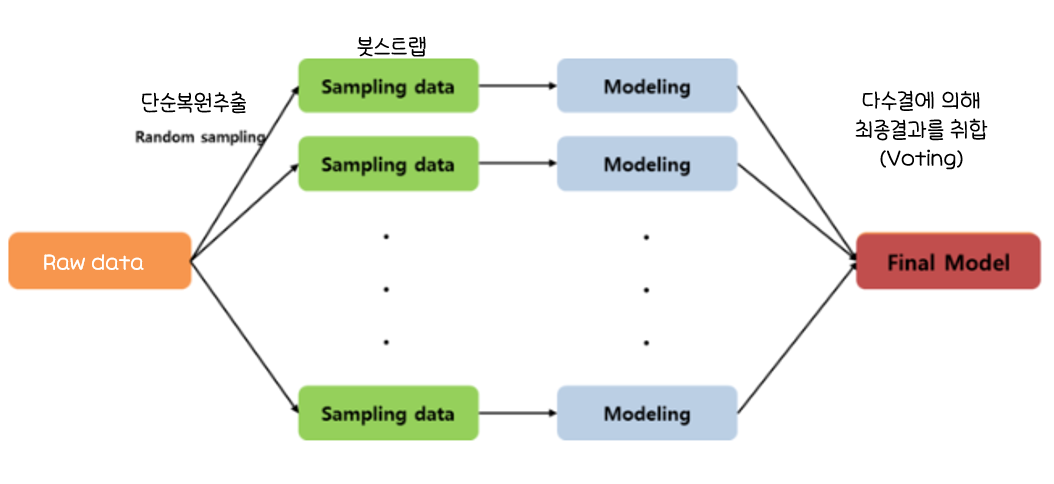
부스팅
예측력이약한 모형(Weak Learner)들을결합하여강한 예측모형을 만드는 방법부스팅 방법중Freund&Schapire가 제안한Adaboost
:이진분류 문제에서랜덤 분류기보다 조금 더 좋은분류기 n개에 각각가중치를 설정하고n개의 분류기를결합하여최종 분류기를 만드는 방법 제안
(단,가중치의 합은 1)훈련오차를빨리 그리고쉽게 줄일수 있음배깅에 비해많은 경우예측오차가향상되어Adaboost의 성능이 배깅보다뛰어남
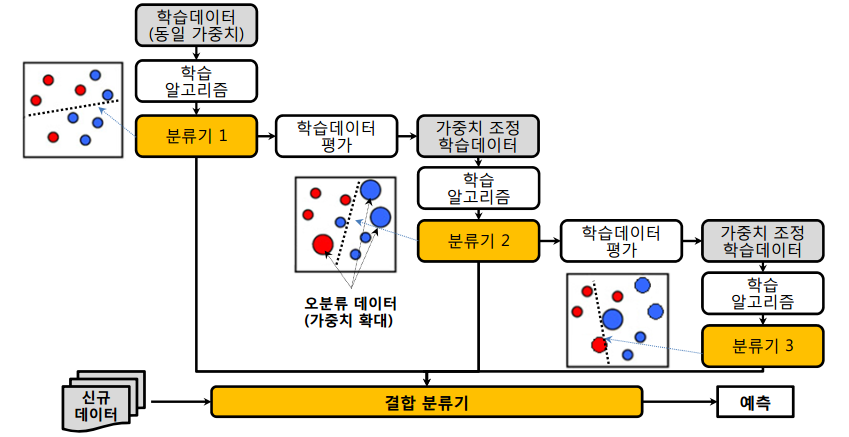
*GBM(Gradient Boosting Machine)
: AdaBoost와 유사하나, 가중치 업데이트시 경사 하강법(Gradient Descent)를 이용
*XGBoost(Extreme Gradient Boosting)
: Gradient Boosted Decision Trees 알고리즘에 기반해 분류, 회귀 등의 모델을 제공하며, GBM에 비해 빠른 수행 시간과 과적합 방지 기능 가짐
*Light GBM
: Tree 기반 학습 알고리즘으로 기존의 다른 Tree기반 알고리즘과 달리 leaf-wise 방식을 따르므로, 속도가 빠르며 큰 사이즈의 데이터를 다룰 수 있고 메모리를 적게 차지
랜덤 포레스트(Random Forest)
Breiman(2001)에 의해 개발의사결정나무의특징인분산이 크다는 점을 고려해배깅과부스팅보다더 많은 무작위성을 주어약한 학습기들을 생성한 후 이를선형 결합하여최종 학습기를 만드는 방법Random Forest 패키지는Random Input에 따른Forest of Tree를 이용한 분류방법랜덤한 Forest에는많은 트리들이 생성수천 개의 변수를 통해변수제거 없이실행되므로정확도 측면에서좋은 성과단점:이론적 설명이나최종 결과에 대한해석이 어렵다장점:예측력이매우 높다. 특히입력변수가 많은 경우,배깅과부스팅과비슷하거나좋은예측력
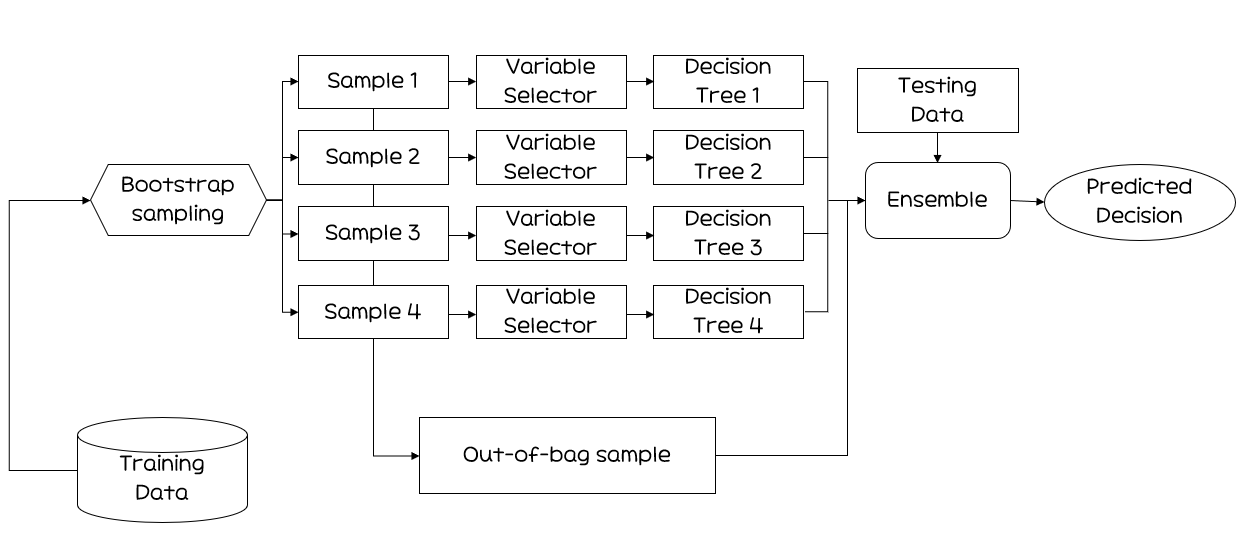
-randomforest 패키지를 이용한 분석
-
모형 만들기
-
오차율 계산하기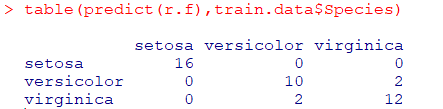
그래프 그리기1

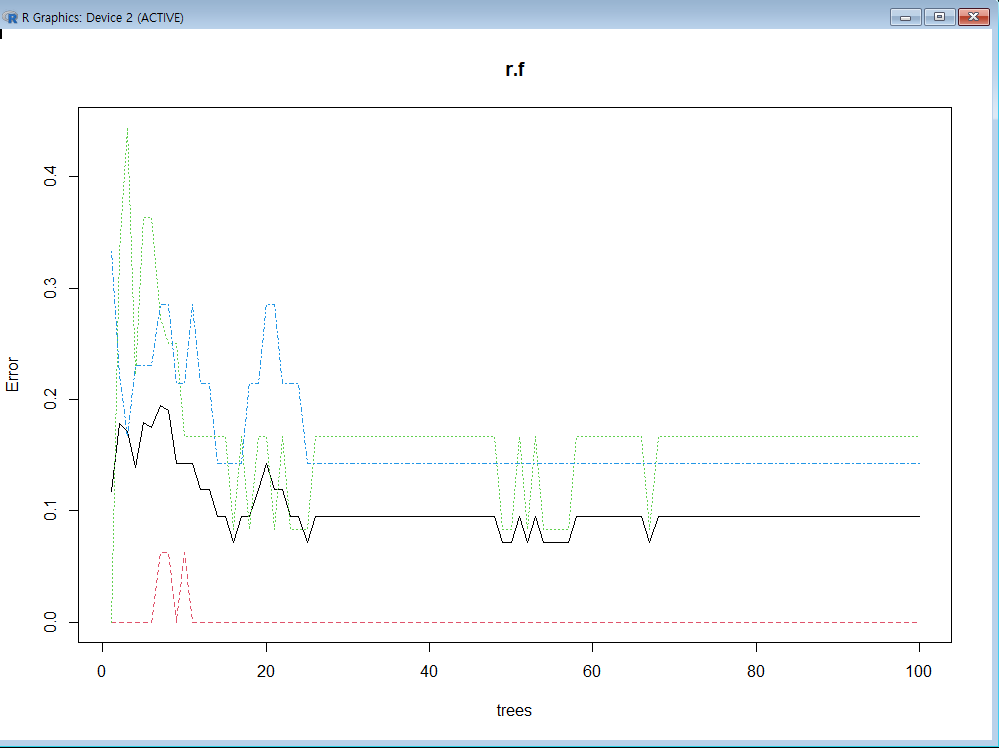
그래프 그리기2

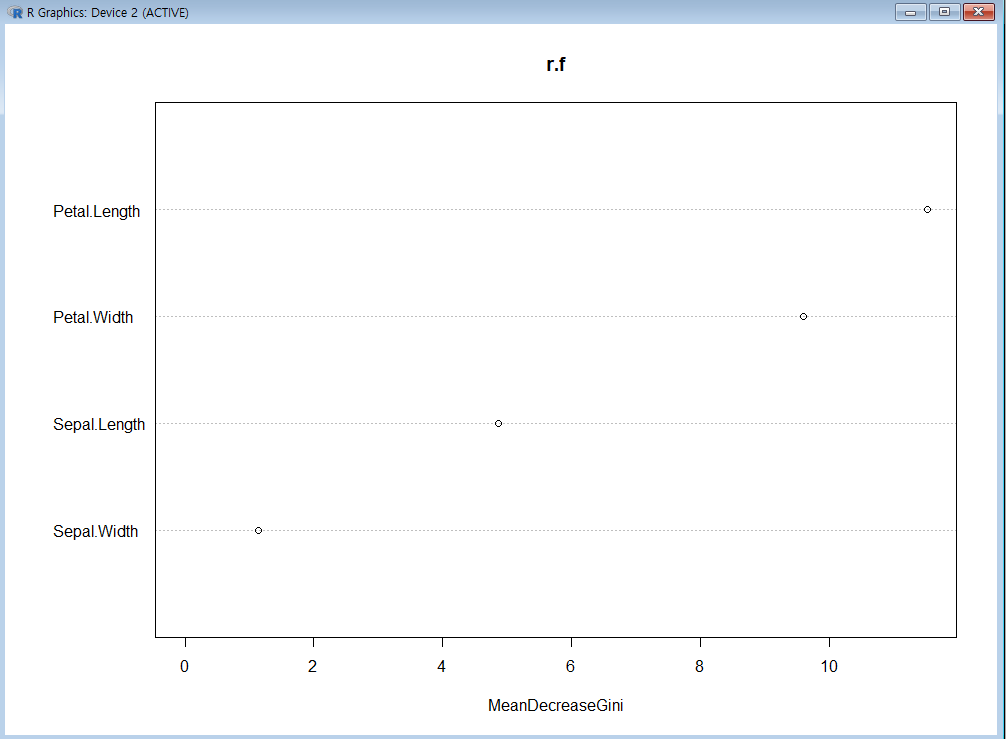
-
test data 예측
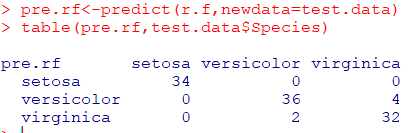
-
그래프 그리기3

🤖인공신경망 분석
인공신경망 분석(ANN)
인공신경망이란?
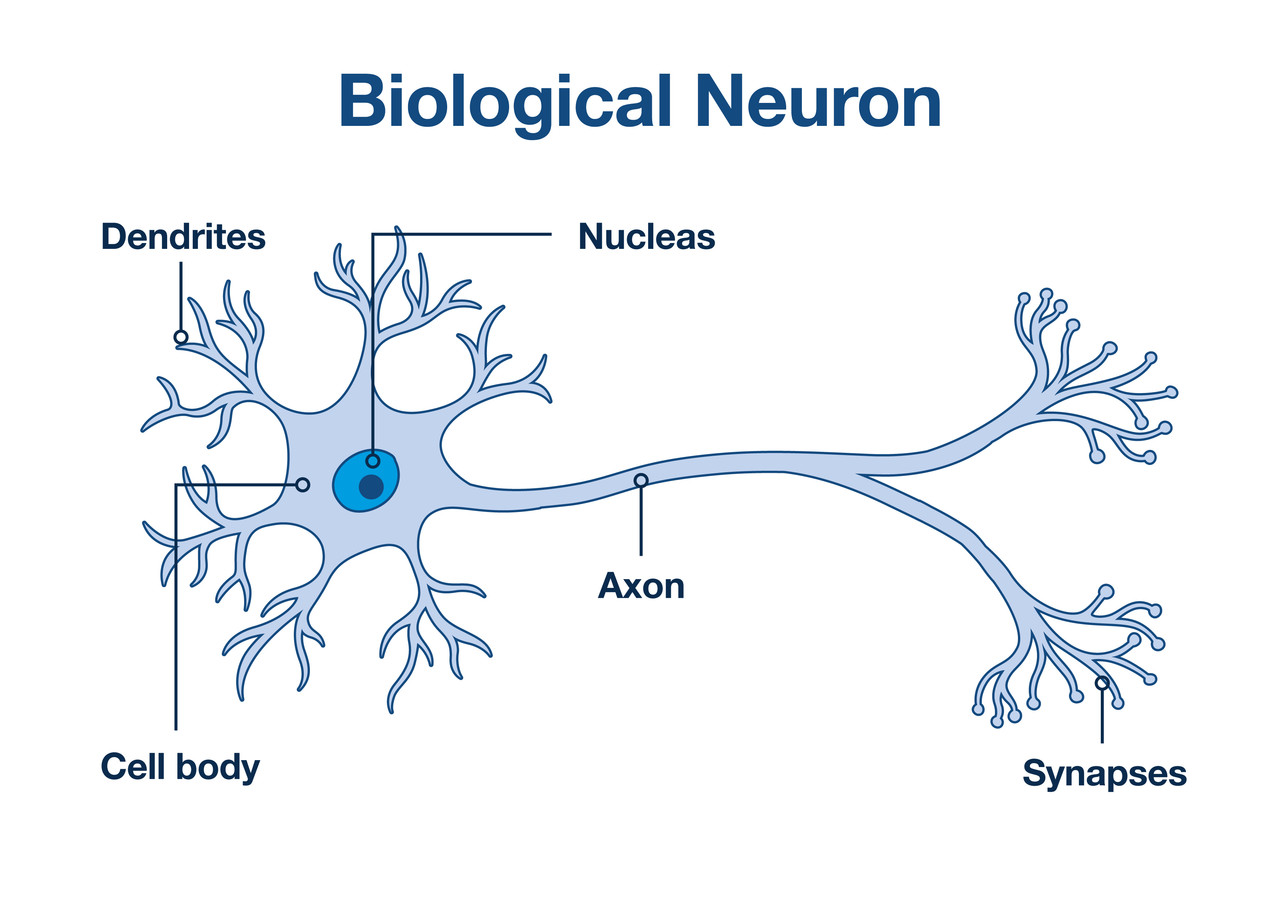
인간 뇌를 기반으로 한추론 모델뉴런: 기본적인정보처리 단위
인공신경망의 연구
1943년매컬럭(McCulloch)과피츠(Pitts)
:인간 뇌를 수 많은신경세포가 연결된하나의 디지털 네트워크 모형으로 간주.신경세포의 신호처리 과정을모형화하여단순 패턴분류 모형개발헵(Hebb):신경세포(뉴런)사이의연결강도(Weight)를 조정하여학습규칙개발로젠블럿(Rosenblatt,1955):퍼셉트론(Perceptron)이라는인공세포개발비선형성의한계점 발생:XOR문제를 풀지 못하는 한계 발견홉필드(Hopfild), 러멜하트(Rumelhart),맥클랜드(McClelland):역전파 알고리즘(Backpropagation)을 활용해비선형성을 극복한다계층 퍼셉트론으로새로운 인공신경망모형 등장
인간의 뇌를 형상화한 인공신경망
인간 뇌 특징
- 100억개의
뉴런, 6조개의시냅스결합체 인간의 뇌는 현존하는 어떤 컴퓨터보다빠르고 매우복잡하고,비선형적이며,병렬적인 정보 처리 시스템과 같음.적응성에 따라'잘못된 답'에 대한뉴런들 사이의 연결은약화,
'올바른 답'에 대한연결 강화
인간의 뇌 모델링
뉴런은가중치가 있는링크들로 연결뉴런은여러 입력 신호를 받지만,출력 신호는오직 하나
인공 신경망의 학습
신경망은가중치를반복적으로 조정하며 학습뉴런은링크(Link)로 연결되어있고, 각링크에는수치적인 가중치가 있음인공신경망은신경망의가중치를초기화하고,훈련 데이터를 통해가중치를 갱신하여신경망의 구조를 선택하고, 활용할학습 알고리즘을 결정 후신경망 훈련
인공신경망의 특징
구조
입력 링크에서여러 신호를 받아서새로운 활성화 수준을 계산하고,출력 링크로출력 신호를 보냄입력신호는미가공 데이터혹은다른 뉴런의 출력출력신호는 문제의최종적인 해또는다른 뉴런의 입력
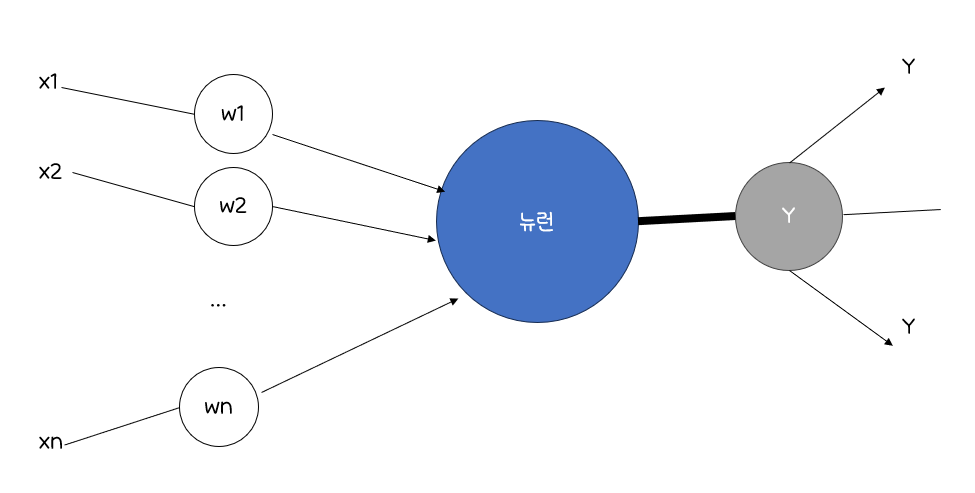
뉴런의 계산
뉴런은전이함수, 즉활성화 함수(Activation Function)사용활성화 함수를 이용해출력을 결정,입력신호의가중치 합을계산하여임계값과 비교가중치 합<임계값:뉴런의 출력은-1가중치 합>=임계값:뉴런의 출력은+1

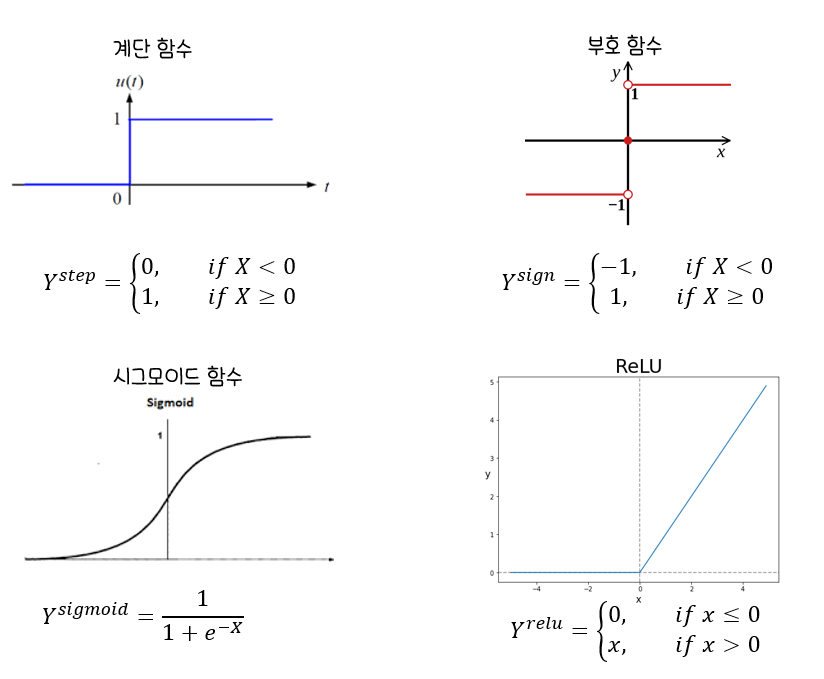
뉴런의 활성화 함수
시그모이드 함수
:로지스틱 회귀분석과유사,0~1의 확률값 가짐
소프트맥스(Softmax) 함수
:표준화지수 함수로 불리며,출력값이여러개로 주어지고
목표치가다범주인 경우,각 범주에 속할사후확률을 제공하는 함수
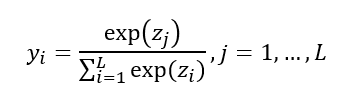
ReLU함수
:입력값이0이하는0,0이상은x값을 가지는 함수.
최근딥러닝에서 많이 활용하는 활성화 함수
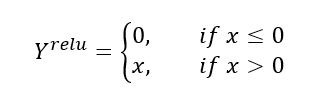
단일 뉴런의학습(단층 퍼셉트론)
퍼셉트론은선형 결합기와하드 리미터로 구성초평면(hyperplane)은n차원 공간을두 개의 영역으로 나눔초평면을선형 분리 함수로 정의
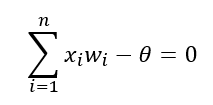
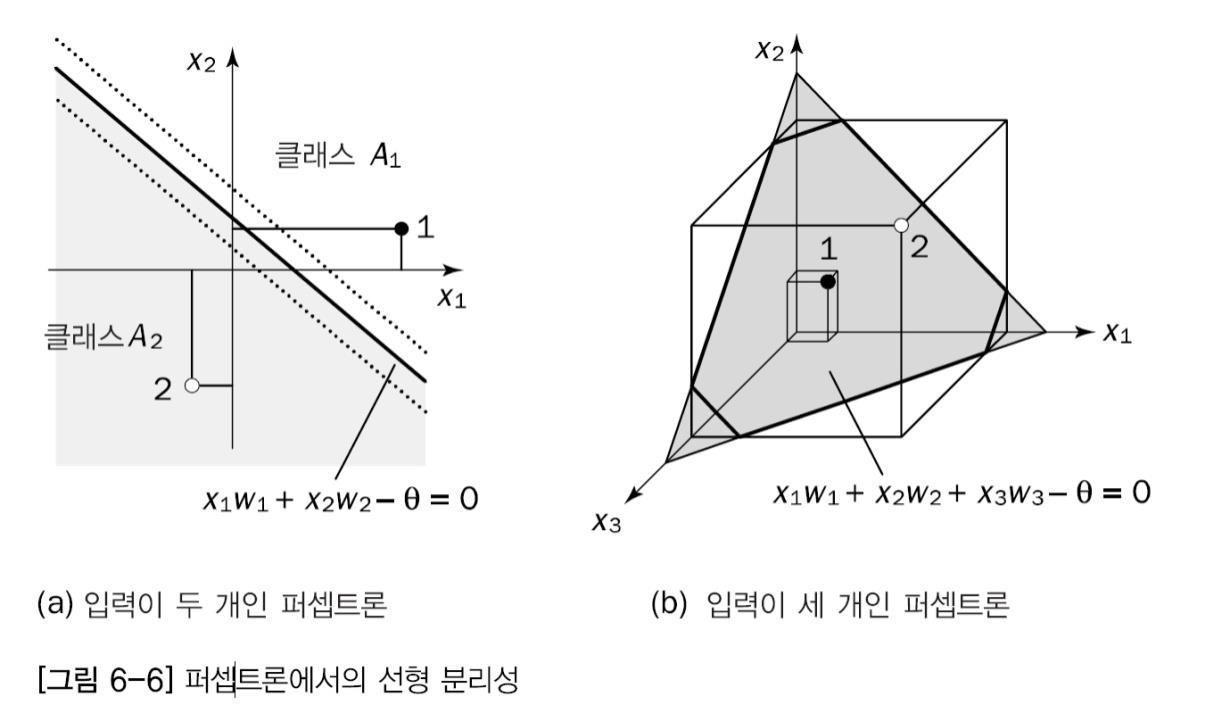
신경망 모형 구축시 고려사항
입력 변수
신경망 모형은복잡성으로 인해입력자료의선택에 매우민감입력변수가범주형또는연속형변수일 때, 아래의 조건이 신경망 모형에 적합
범주형 변수 : 모든 범주에서 일정 빈도 이상의 값을 갖고, 각 범주의 빈도가 일정할 때
연속형 변수 : 입력변수 값들의 범위가 변수간의 큰 차이가 없을 때연속형 변수의 경우그 분포가평균을 중심으로대칭이 아니면,좋지 않은 결과를 도출하므로 아래와 같은 방법 활용
변환 : 고객의 소득(대부분 평균미만이고, 특정 고객의 소득이 매우 큰) : 로그변환
범주화 : 각 범주의 빈도가 비슷하게 되도록 설정범주형 변수의 경우가변수화하여적용(ex. 남녀:1, 0 또는 1,-1) 하고,
가능하면모든 범주형 변수는같은 범위를 갖도록가변수화
가중치의 초기값과다중 최소값 문제
역전파 알고리즘은초기값에 따라결과가 많이 달라지므로초기값의 선택이 매우 중요가중치가0이면,시그모이드 함수는선형이 되고,
신경망 모델은근사적으로 선형모형이 됨- 일반적으로
초기값은0 근처로 랜덤하게 선택하므로,초기 모형은선형 모형에 가깝고,가중치 값이증가할수록비선형모형이 됨
(초기값이0이면,반복해도값이 전혀 변하지 않고,너무 크면좋지 않은 해를 주는 문제점을 내포하고 있어 주의 필요)
*기울기 소실(Gradient Vanishing)
: 깊은 인공신경망에서 역전파 과정에서 입력층으로 갈수록 기울기가 점차 작아져 가중치 업데이트가 안되는 현상
*일반화 가중치(Generalized Weights)
: 각 공변량들의 효과를 나타내는 것으로, 로지스틱 회귀모형에서의 회귀계수와 유사하게 해석
(각 공변량의 로그-오즈에 미치는 기여도)
학습모드
온라인 학습 모드(Online Learning Mode)- 각 관측값을
순차적으로하나씩 신경망에 투입하여가중치 추정값이 매번 바뀜 속도가 빠르며, 특히훈련자료에유사값이 많은 경우, 그차이가 더 두드러짐훈련자료가비정상성(Nonstationarity)과 같이특이한 성질을 가진경우가 좋음국소최솟값에서벗어나기가 더 쉬움
- 각 관측값을
-
확률적 학습 모드(Probabilistic Learning Mode)온라인 학습 모드와 같으나,신경망에투입되는관측값의 순서가 랜덤
-
배치 학습 모드(Batch Learning Mode)전체 훈련자료를동시에신경망에 투입
*학습률(Learning Rate)
: 처음에는 큰 값으로 정하고, 반복 수행과정을 통해 해에 가까울수록 학습률이 0에 수렴
은닉층(Hidden Layer)과은닉 노드(Hidden Node)의수
신경망을 적용할 때 가장 중요한 부분이모형의 선택(은닉층의 수, 은닉노드의 수 결정)은닉층과은닉노드가많으면,가중치가 많아져서과대 적합 문제발생은닉층과은닉노드가적으면,과소적합 문제발생은닉층의 수가하나인신경망은범용 근사자(Universal Approximator)이므로,모든 매끄러운 함수를근사적으로표현할 수 있음.
=> 가능하면은닉층은하나은닉노드의 수는적절히 큰 값으로 놓고,가중치를 감소(Weight Decay)시키며 적용하는 것이 좋음.
과대 적합 문제
- 신경망에서는
많은 가중치를추정해야 하므로과대적합 문제가빈번 알고리즘의 조기종료와가중치 감소 기법으로해결모형이 적합하는 과정에서검증오차가 증가하기 시작하면,반복을 중지하는조기종료시행선형모형의능형회귀(릿지회귀)와 유사한,가중치 감소라는벌점화 기법활용
*포화문제
: 작은 기울기는 곧 학습 능력이 제한된다는 것을 의미하고, 이를 일컬어 신경망에 포화가 발생했다고 함.
포화가 일어나지 않게 하기 위해 입력값을 작게 유지해야 함
*딥러닝(Deep Learning)
: 머신러닝의 한 분야. 인공신경망의 한계를 극복하기 위해 제안된 심화신경망을 활용한 방법
- 음성, 이미지 인식, 자연어 처리, 헬스 케어 등의 전반적인 분야에 활용
*딥러닝 소프트웨어
TensorflowCaffeTheanoMXnet
👥군집분석
군집분석
- 각 객체의
유사성을 측정해유사성이 높은 대상 집단을분류하고,
군집에 속한 객체들의유사성과서로 다른 군집에 속한 객체간의상이성을 규명하는 분석 방법 특성에 따라 고객을여러 개의 배타적인 집단으로 나누는 것결과는 구체적인군집분석 방법에 따라차이가 남군집의 개수나구조에 대한 가정없이데이터들 사이의거리를 기준으로 군집화 유도- ex) 마케팅 조사에서
소비자들의 상품 구매 행동,라이프스타일에 따른소비자군을 분류하여 시장 전략 수립 등
특징
요인분석과의차이점
요인분석:유사한 변수를 함께 묶어주는 것이 목적
판별분석과의차이점
판별분석:사전에집단이 나누어져 있는 자료를 통해새로운 데이터를기존의 집단에할당하는 것이 목적
거리
군집분석에서는관측 데이터 간유사성이나근접성을 측정해어느 군집으로묶을수 있는지 판단해야 함.
연속형 변수의 경우
유클리디안 거리(Euclidean Distance)
: 데이터간의유사성을 측정할 때많이 사용하는 거리통계적 개념이내포되어 있지 않아변수들의산포 정도가 전혀 감안X
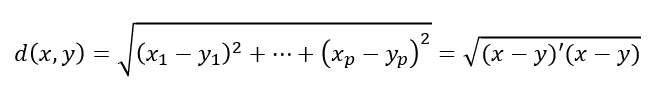
표준화 거리(Statistical Distance)
: 해당변수의표준편차로척도 변환후유클리디안 거리를 계산표준화하게 되면척도의 차이,분산의 차이로 인한왜곡 피함
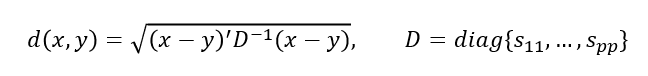
마할라노비스(Mahalanobis) 거리
:통계적 개념이포함된 거리이며변수들의 산포를 고려하여 이를표준화한 거리(Standardized Distance)두 벡터 사이의 거리를산포를 의미하는 표본공분산으로나눠줘야 하며, 그룹에 대한 사전 지식 없이는표본공분산S를 계산할 수 없으므로 사용하기 곤란변수의 표준화와변수 간의 상관성을 동시에 고려
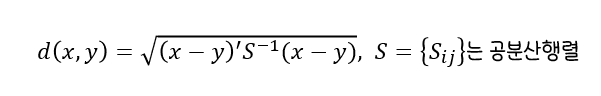
체비셰프(Chebychev) 거리
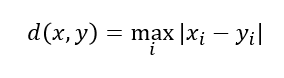
맨하탄(Manhattan) 거리
: 유클리디안 거리와 함께 가장 많이 사용되는 거리로,
맨하탄 도시에서건물에서 건물을 가기 위한 최단 거리를 구하기 위해 고안된 거리- 데이터에
이상치가 존재한다고 여겨지고그것들을 제거할 수 없는 경우에 사용
=>ROBUST(이상치로 부터 영향X)한 측도
- 데이터에
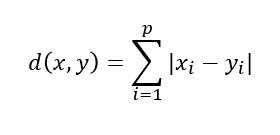
캔버라(Canberra) 거리
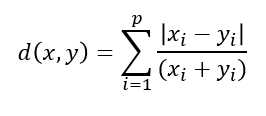
민코우스키(Minkowski) 거리
:맨하탄 거리와유클리디안 거리를한번에 표현한 공식L1 거리(맨하탄 거리),L2 거리(유클리디안 거리)
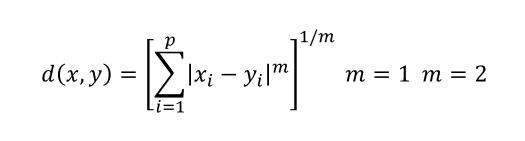
범주형 변수의 경우
자카드 거리
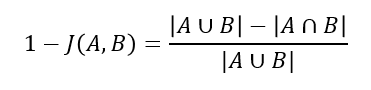
자카드 계수
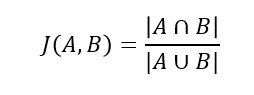
*자카드 계수 기반 유사도
: Boolean 속성으로 이루어진 두 개의 오브젝트 A, B에 대하여 A와 B가 교집합으로 1의 값을 가진 속성의 개수를 A와 B의 1의 합집합 개수로 나눈 값
코사인 거리
:문서를유사도기준으로분류혹은그룹핑시 유용
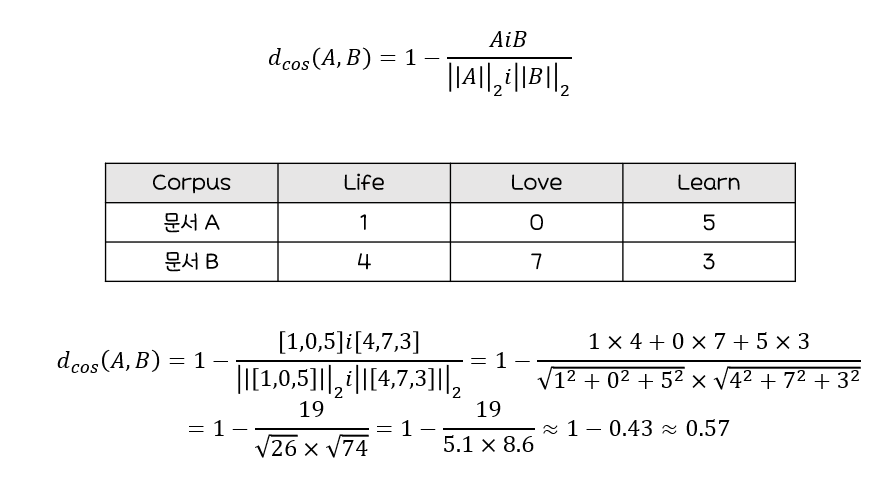
코사인 유사도
:두 개체의백터 내적의코사인 값을 이용해 측정된벡터간의 유사한 정도
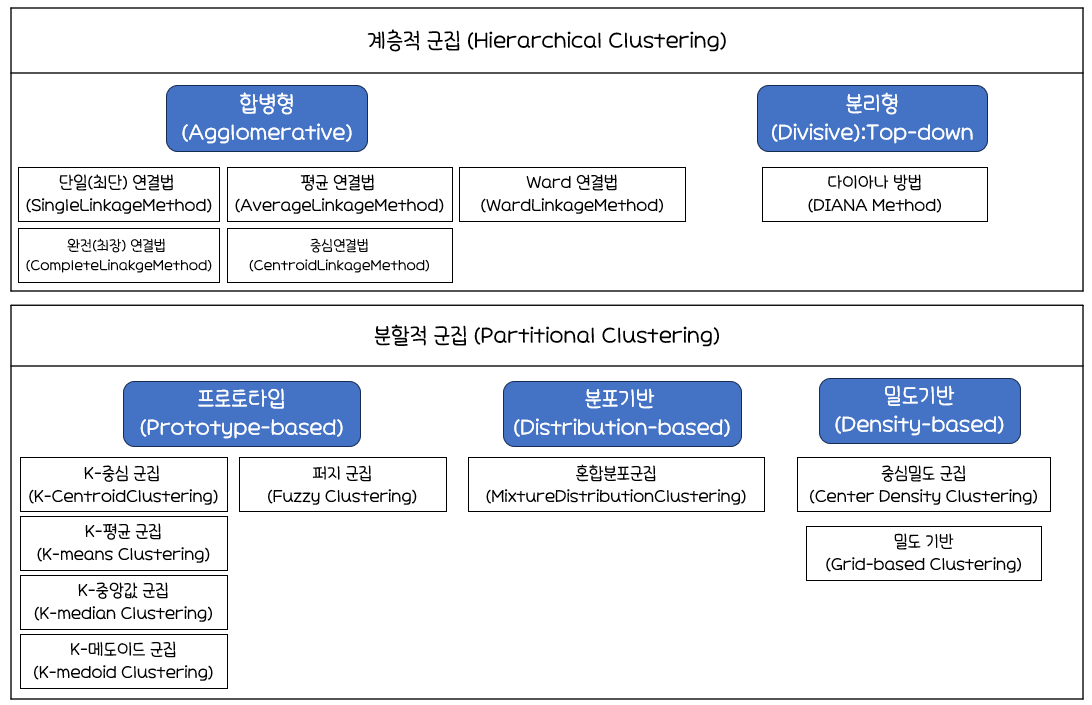
계층적 군집분석
n개의 군집으로 시작해점차 군집의 개수를 줄여 나가는 방법계층적 군집을 형성하는 방법합병형(응집형) 방법(Agglomerative : Bottom-Up)
: 관측값을 각각하나의 군집으로 보고, 관측값 특성이가까운 군집끼리순차적으로 합해가는 방식분리형 방법(Divisive : Top-Down)
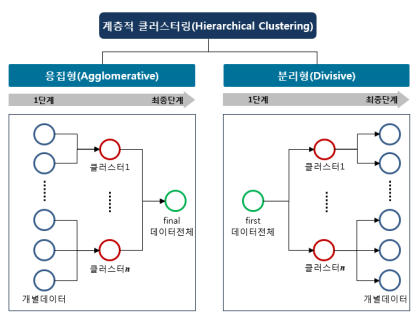
최단연결법(Single Linkage)
: 군집과 군집 또는 데이터와의 거리 계산 시 최단거리(min)를 거리로 계산
n*n 거리행렬에서거리가 가장 가까운 데이터를 묶어서 군집 형성수정된 거리행렬에서거리가 가까운 데이터또는군집을 새로운 군집으로 형성사슬 모양으로 군집이 생길 수 있음고립된 군집을 찾는데 중점
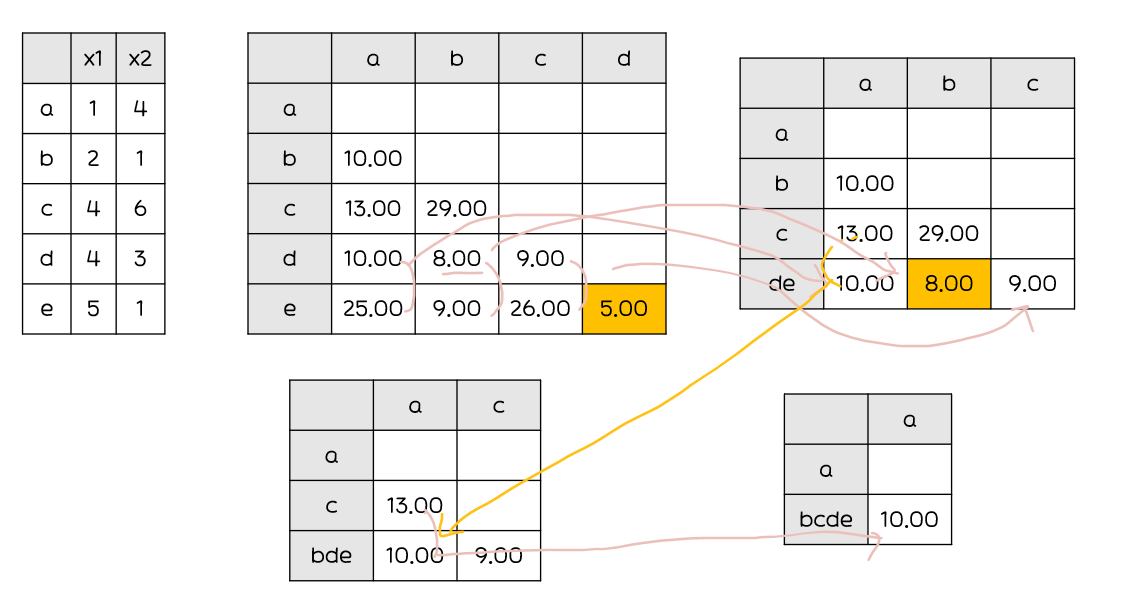
최장연결법(Complete Linkage)
: 군집과 군집 또는 데이터와의 거리 계산 시 최장거리(max)를 거리로 계산하여 거리 행렬을 수정
군집들의내부 응집성에 중점
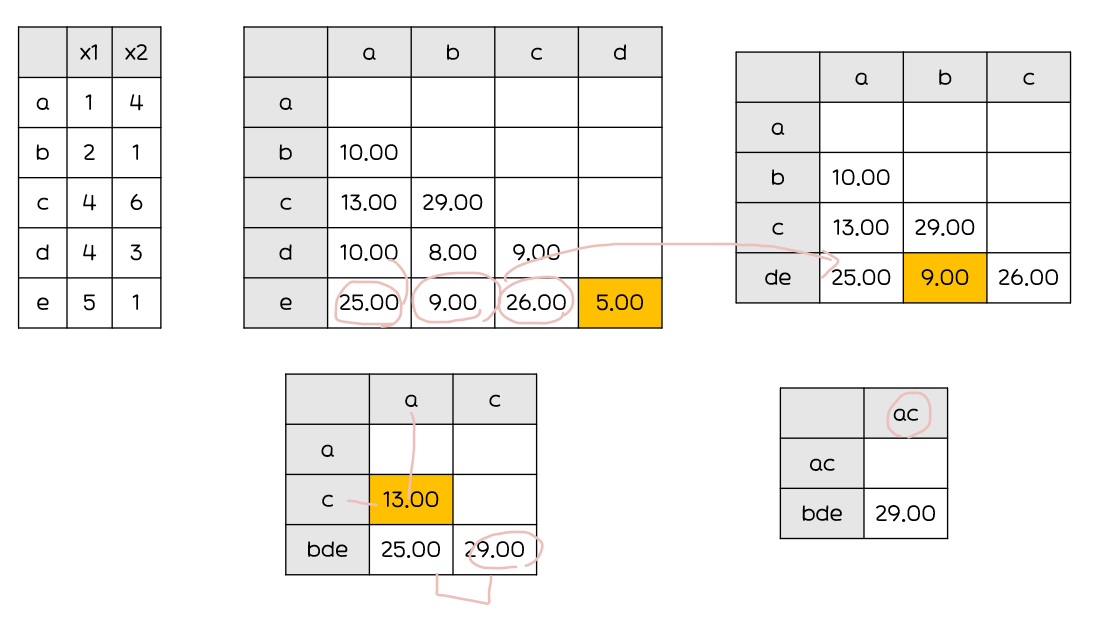
평균연결법(Average Linkage)
: 군집과 군집 또는 데이터와의 거리 계산 시 평균(mean)을 거리로 계산하여 거리 행렬을 수정
계산량이불필요하게 많아짐
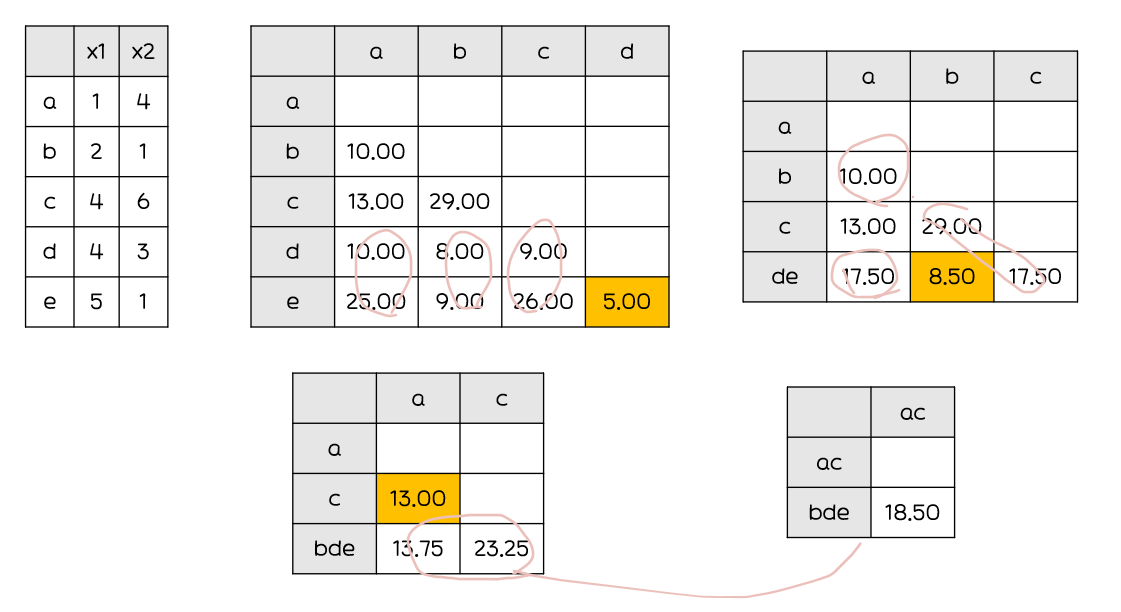
중심 연결법(Centroid Linkage)
: 두 군집의 중심간 거리를 군집간 거리로 하며, 군집이 결합될 때 새로운 군집의 평균은 가중평균을 통해 구해짐
와드연결법(Ward Linkage)
: 군집내 편차들의 제곱합을 고려한 방법
- 군집 간 정보의
손실을최소화하기 위해 군집화 진행
군집화
거리행렬을 통해가장 가까운 거리의 객체들간의 관계를 규명하고덴드로그램을 그림덴드로그램을 보고군집의 개수를 변화해가며 적절한군집 수 선정군집의 수는 분석 목적에 따라 선정할 수 있으나,대부분 5개 이상의 군집은 잘 활용 X군집화 단계
1.거리행렬을 기준으로덴드로그램을 그린다.
2.덴드로그램의최상단부터세로축의 개수에 따라가로선을 그어군집의 개수선택
3.각 객체들의 구성을 고려해적절한 군집 수선정
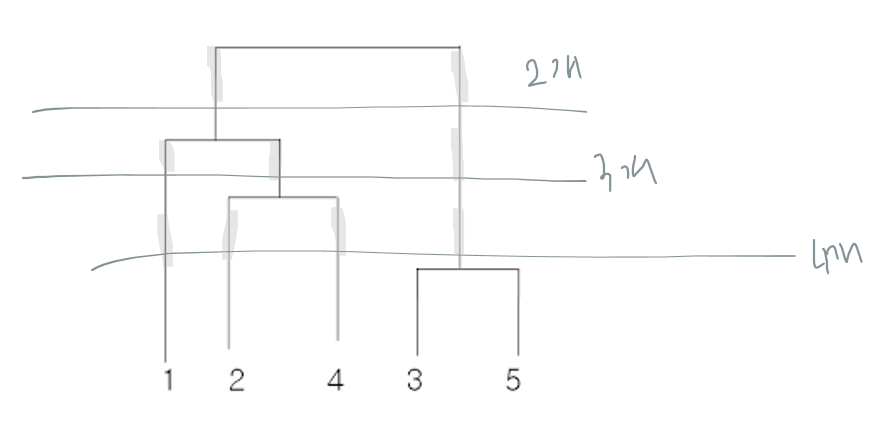
비계층적 군집분석
n개의 개체를k개의 군집으로 나눌 수 있는모든 가능한 방법을 점검해최적화한 군집을 형성하는 것
Fuzzy Clustering
: 퍼지이론에 기반하여 각 관측치가 여러 군집에 동시에 속할 수 있으며, 각 군집별로 속할 가능성을 제시
밀도기반 군집(Density-Based Clustering)
: 동일 군집에 속하는 데이터는 서로 근접하게 분포할 것이라는 가정을 기반으로 한 군집분석
- ex)
DBSCAN,OPTICS,DENCLUE,STING
k-평균 군집분석(k-Means Clustering)의 개념
- 주어진
데이터를k개의 클러스터로 묶는 알고리즘 각 클러스터와거리의 차이의분산을최소화하는 방식으로 동작
k-평균 군집분석(K-Means Clustering) 과정
- 원하는
군집의 개수와초기 값(seed)들을 정해seed중심으로 군집 형성 - 각 데이터를
거리가 가장 가까운 seed가 있는 군집으로분류 - 각 군집의
seed값을다시 계산 모든 개체가군집으로 할당될 때까지 위 과정 반복
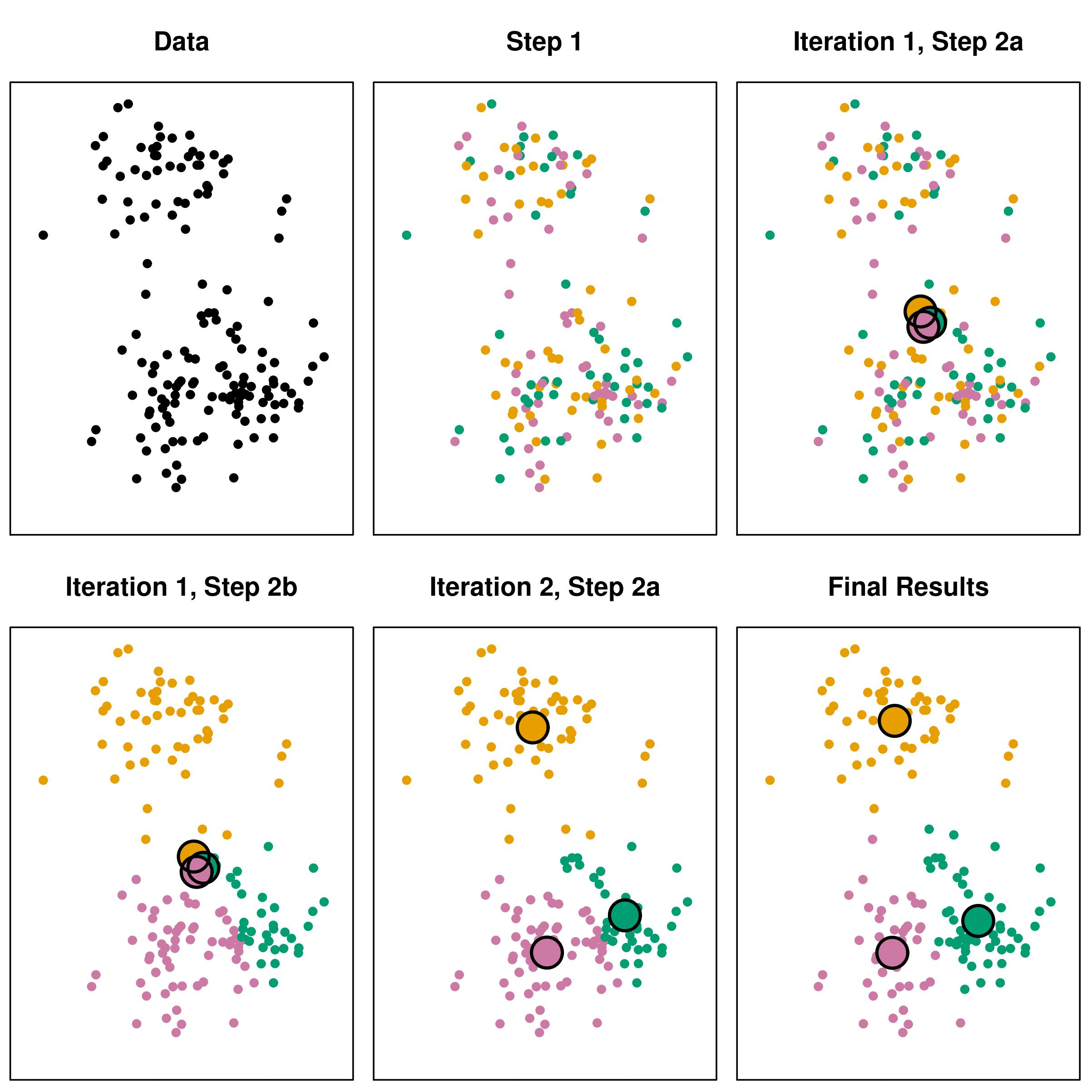
k-평균 군집분석의 특징
거리 계산을 통해군집화가 이뤄지므로연속형 변수에 활용 가능k개의초기 중심값(seed)은임의로 선택 가능하며 가급적이면멀리 떨어지는 것이 바람직초기 중심값을 임의로 선택시일렬(상하, 좌우)로 선택하면,군집 혼합이 되지 않고층으로 나누어질 수 있어 주의초기 중심값의선정에 따라결과 달라짐초기 중심으로부터의오차 제곱합을최소화하는 방향으로 군집이 형성되는탐욕적(Greedy) 알고리즘
=>안정된 군집은보장하나,최적이라는보장X
| 장점 | 단점 |
|---|---|
| - 알고리즘이 단순 - 빠르게 수행되어 분석 방법 적용 용이 - 계층적 군집분석에 비해 많은 양의 데이터를 다룰 수 있음 - 내부 구조에 대한 사전정보가 없어도 의미있는 자료구조 찾기 가능 - 다양한 형태의 데이터에 적용 가능 | - 군집의 수, 가중치와 거리 정의가 어려움 - 사전에 주어진 목적이 없어 결과 해석이 어려움 - 잡음이나 이상값 영향 많이 받음 - 볼록한 형태가 아닌(Non-Convex) 군집(ex. U형태) 존재시 성능이 떨어짐 - 초기 군집 수 결정에 어려움 |
PAM(Partitioning Around Medoids)/k-medoid Clustering
Medoid: 한 클러스터의 개체인데, 이 개체가속한 클러스터 내에서의 다른모든 개체들과의 평균거리가가장 작은 개체k-means Clustering의이상값(Outlier)에민감해경계 설정이 어렵다는단점을 극복하기 위한 군집 방법
혼합 분포 군집(Mixture Distribution Clustering)
모형 기반(Model-Based)의 군집 방법- 데이터가
k개의모수적 모형(흔히 정규분포 또는 다변량 정규분포를 가정)의 가중합으로 표현되는모집단 모형으로부터 나왔다는 가정하에모수와 함께가중치를 자료로부터추정하는 방법 사용 k개의각 모형은군집을 의미하며, 각 데이터는추정된 k개의 모형중어느 모형으로부터나왔을 확률이 높은지에 따라군집의 분류가 이뤄짐- 흔히
혼합모형에서모수와가중치의 추정(최대가능도추정)에는EM알고리즘사용
혼합 분포모형으로 설명할 수 있는 데이터의 형태
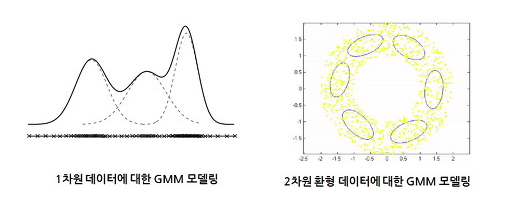
- 첫번째는
자료의 분포형태가다봉형의 형태를 띄므로단일 분포로의적합은적절하지 않으며, 대략3개정도의정규분포 결합을 통해 설명 - 두번째의 경우,
여러 개의 이변량 정규분포의결합을 통해 설명 - 두 경우 모두
반드시 정규분포로 제한할 필요X
EM(Expectation-Maximization) 알고리즘 진행 과정
각 자료에 대해Z의 조건부분포(어느 집단에 속할지에 대한)로부터조건부 기댓값을 구함관측변수 X와잠재변수 Z를 포함하는(X,Z)에 대한로그-가능도 함수(이를 보정된(Augmented) 로그-가능도함수라 함)에Z대신상수값인 Z의 조건부 기댓값을 대입하면,로그-가능도함수를최대로 하는모수를 쉽게 찾을 수 있음(M-단계)갱신된 모수 추정치에 위 과정을 반복하면,수렴하는 값을 얻게 되고, 이는최대 가능도 추정치로 사용E-단계:잠재변수 Z의기대치 계산M-단계:잠재변수 Z의기대치를 이용하여파라미터 추정
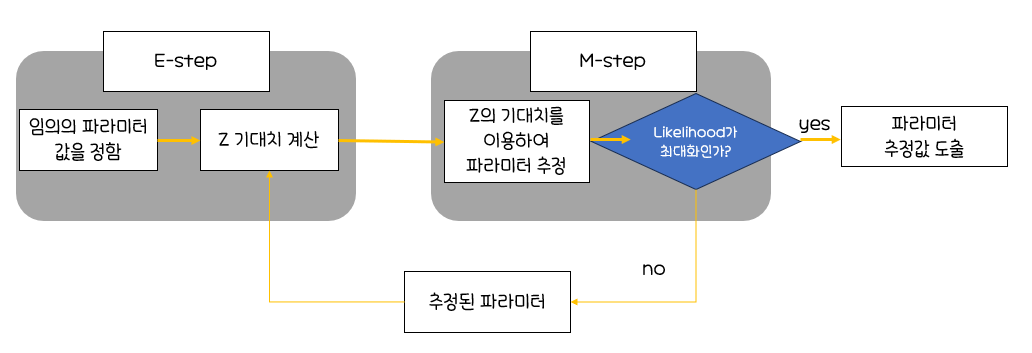
EM알고리즘의 진행과정
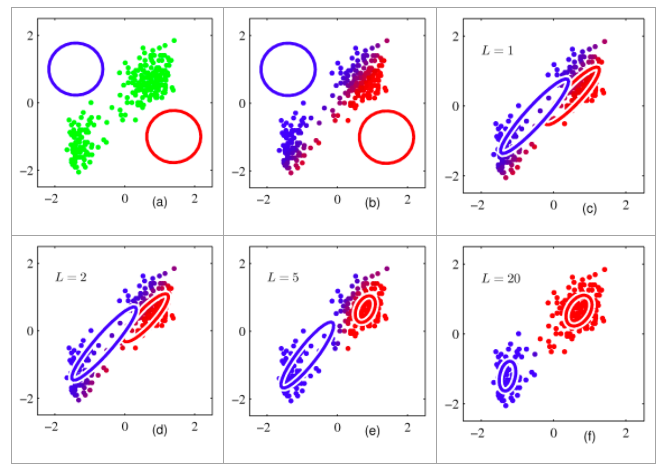
혼합 분포 군집모형의특징
k-평균 군집의 절차와 유사하나,확률분포를도입하여군집 수행군집을몇 개의 모수로 표현할 수 있으며,서로 다른 크기나모양의 군집을 찾을 수 있음EM알고리즘을 이용한모수 추정에서데이터가 커지면수렴에 시간이 걸림군집의 크기가너무 작으면추정의 정도가떨어지거나어려움k-평균 군집과 같이이상치 자료에민감
SOM(Self Organizing Map)
자기조직화지도(Self Organizing Map, SOM)는코호넨(Kohonen)에 의해 제시, 개발되었으며코호넨 맵(Kohonen Maps)라고도 함비지도 신경망고차원의 데이터를 이해하기 쉬운저차원의 뉴런으로 정렬하여지도의 형태로 형상화
-> 이런 형상화는입력 변수의위치 관계를그대로 보존
=>실제 공간의 입력 변수가가까이있으면,지도상에도가까운 위치
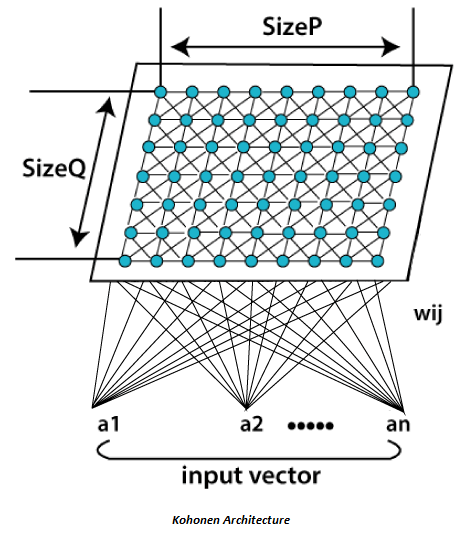
구성
: SOM모델은 두 개의 인공신경망 층으로 구성
입력층(Input Layer : 입력벡터를 받는 층)
입력 변수의개수와동일하게뉴런 수존재입력층의 자료는학습을 통하여경쟁층에 정렬되는데, 이를지도(Map)라 부름입력층에 있는 각각의뉴런은경쟁층에 있는 각각의뉴런들과연결되어 있으며, 이 때완전 연결(Fully Connected)됨
경쟁층(Competitive Layer : 2차원 격자(Grid)로 구성된 층)
입력벡터의특성에 따라벡터가한 점으로클러스터링되는 층SOM은경쟁 학습으로 각각의뉴런이입력 벡터와얼마나 가까운가를 계산하여연결 강도(Connection Weight)를반복적으로 재조정하여 학습
->연결강도는입력 패턴과가장 유사한 경쟁층 뉴런이 승자입력 층의표본 벡터에 가장가까운 프로토타입 벡터를 선택해BMU(Best-Matching-Unit이라고 함.코호넨의 승자 독점의 학습 규칙에 따라위상학적 이웃(Topological Neighbors)에 대한연결 강도를 조정승자 독식 구조로 인해경쟁층에는승자 뉴런만 나타남승자와 유사한 연결 강도를 갖는입력 패턴이동일한 경쟁 뉴런으로 배열
특징
고차원의 데이터를저차원의 지도 형태로 형상화하기 때문에시각적으로 이해가 쉬움입력 변수의위치 관계를그대로 보존하기 때문에실제 데이터가 유사하면지도상에서도 가깝게 표현
-> 이 특징으로패턴 발견,이미지 분석등에서 뛰어남역전파(Back Propagation) 알고리즘등을 이용하는인공신경망과 달리,
단 하나의 전방 패스(Feed-Forward Flow)를 사용하여속도가 매우 빠름
->실시간 학습처리가능
SOM vs 신경망 모형
| 구분 | 신경망 모형 | SOM |
|---|---|---|
| 학습 방법 | 오차역전파법 | 경쟁학습방법 |
| 구성 | 입력층,은닉층,출력층 | 입력층,경쟁층 |
| 기계학습 방법의 분류 | 지도학습 | 비지도 학습 |
최신 군집분석 기법들
Hierarchical Clustering(계층적 군집)
#dim은 dataframe의 길이 관측시 사용. 행, 열 반환
#dim(iris[1]) : 행 150개
idx<-sample(1:dim(iris)[1],40)
iris.s<-iris[idx,]
#Species 안보이게 함
iris.s$Species<-NULL
#hclust : 계층 군집
#dist : 거리 계산
#평균연결법
hc<-hclust(dist(iris.s),method="ave")
#hang 옵션 : 레이블이 나머지 플롯 아래에 있어야 하는 플롯의 높이 비율
plot(hc,hang=-1,labels=iris$Species[idx])
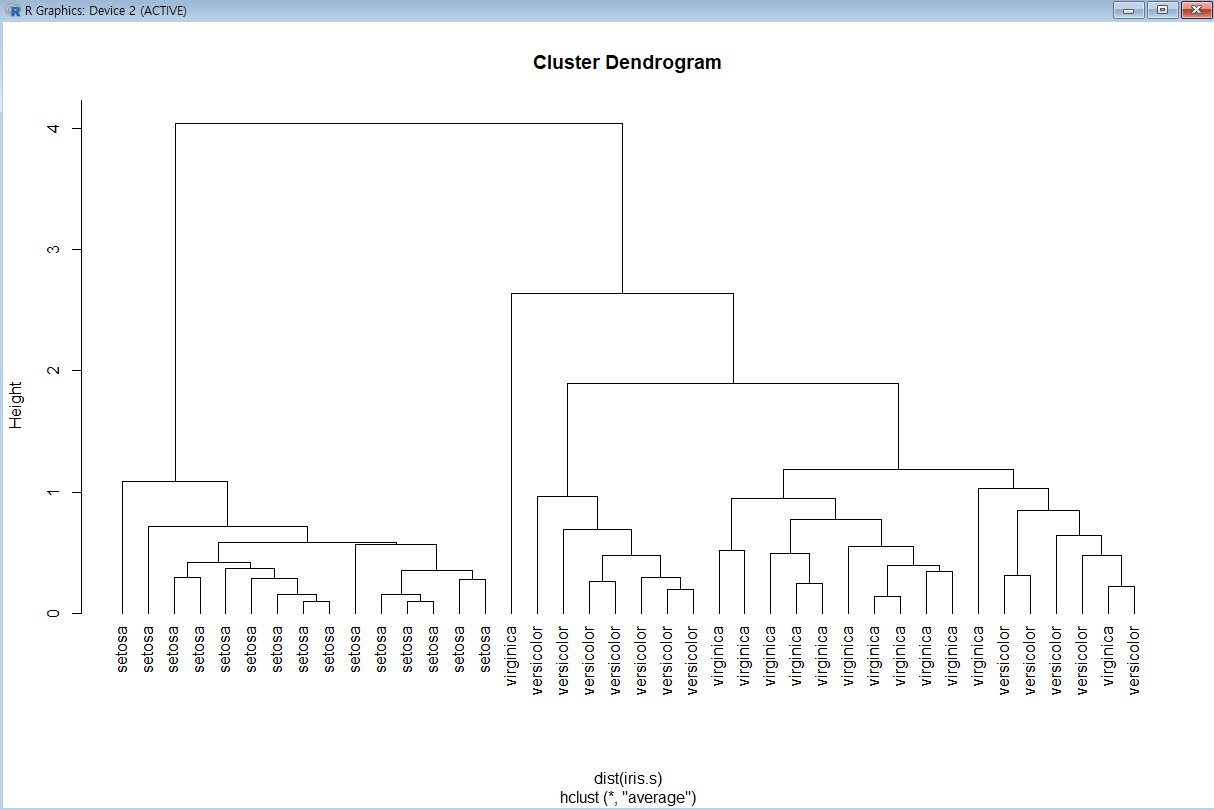
*dist()
: 데이터 행렬의 행 사이의 거리를 계산하기 위해 지정된 거리 측도를 사용해 계산된 거리 행렬을 계산
"euclidean","maximum","manhattan","canberra","binary","minkowski"
k-Means Clustering
: 비계층적 군집방법
군집화
data(iris)
newiris<-iris
newiris$Species<-NULL
#군집을 3개 만듦
kc<-kmeans(newiris,3)
-
결과비교
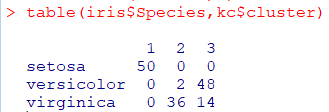
-
군집화 그래프

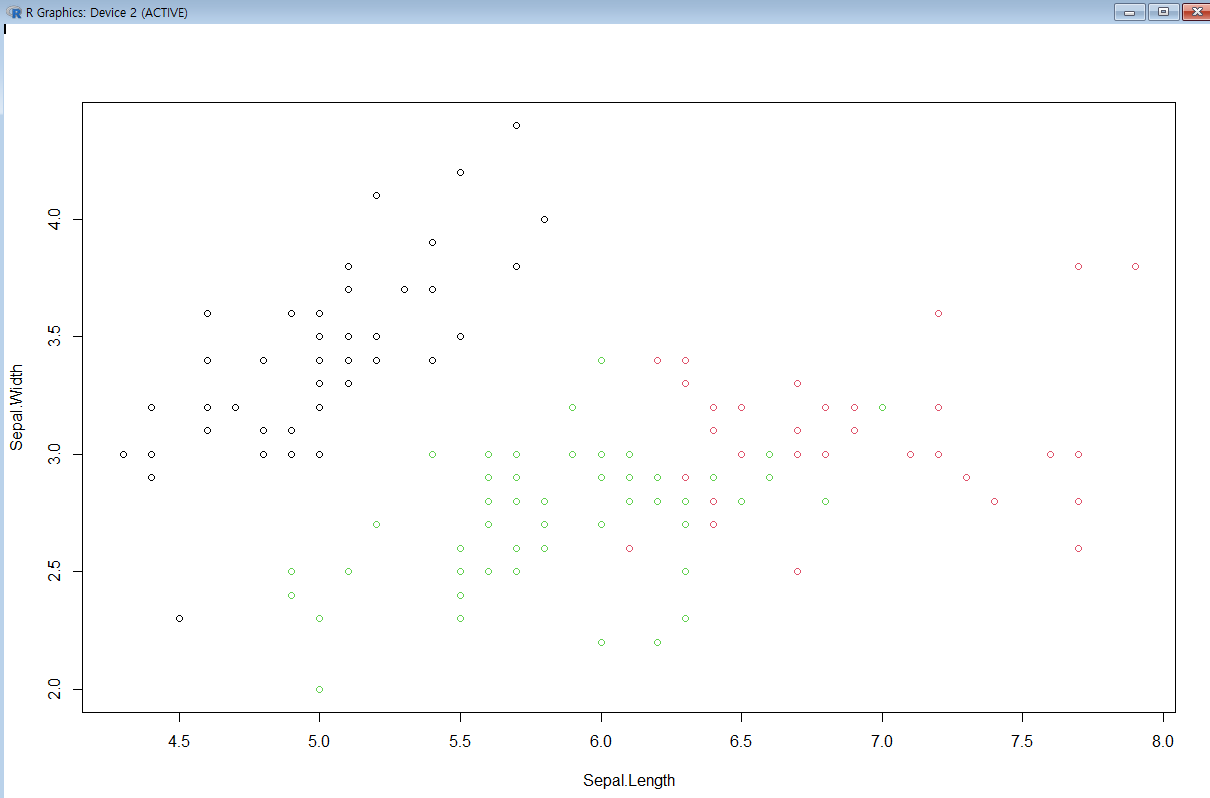
🐱🐉연관분석
연관규칙
연관규칙분석(Association Analysis)의 개념
장바구니분석(Market Basket Analysis)또는서열분석(Sequence Analysis)라 불림- 기업의 데이터베이스에서 상품의 구매, 서비스 등
일련의 거래또는사건들 간의규칙 발견을 위해 적용 장바구니 분석: 장바구니에 무엇이같이 들어있는지에 대한 분석서열분석:A를 산 다음에B를 산다
연관규칙의 형태
조건과반응의 형태(if-then)
(Item set A)->(Item set B)
if A then B #만일 A가 일어나면, B가 일어난다
#아메리카노를 마시는 손님 중 10%가 브라우니를 먹는다
#샌드위치를 먹는 고객의 30%가 탄산수를 함께 마신다연관규칙의 측도
지지도(Support)
:전체 거래 중항목A와 항목B를 동시에 포함하는 거래의 비율

신뢰도(Confidence)
:항목 A를 포함한 거래중에서항목A와 항목B가 같이 포함될 확률연관성의 정도 파악

향상도(Lift)
:A가 구매되지 않았을 때 품목 B의 구매확률에 비해A가 구매됐을 때 품목 B의 구매확률의 증가 비연관규칙 A->B는품목A와품목B의구매가 서로 관련이 없는 경우에향상도 1

연관규칙의 절차
-
최소 지지도보다큰집합만을 대상으로높은 지지도를 갖는 품목 집합을 찾음 -
처음에는
5%로 잡고, 규칙이 충분히 도출되는지 보고 다양하게 조절 -
처음부터
너무 낮은 최소 지지도를 선정하는 것은많은 리소스 소모로 적절X -
절차
1.최소 지지도결정
2.품목 중최소 지지도를 넘는 품목 분류
3.2가지 품목 집합생성
4.반복적으로 수행해빈발품목 집합을 찾음
연관규칙의 장점과 단점
장점
탐색적인 기법으로조건 반응으로 표현되는 연관성 분석의결과를쉽게 이해강력한 비목적성 분석기법으로분석 방향이나목적이 특별히 없는 경우목적변수(y)가 없으므로 유용하게 활용사용이편리한 분석 데이터의 형태로 거래 내용에 대한데이터를 변환 없이그 자체로이용할 수 있는 간단한 자료 구조분석을 위한 계산 간단
단점(개선방안)
품목수가 증가하면분석에 필요한 계산이기하급수적으로 늘어남
-> 개선을 위해유사한 품목을한 범주로일반화
->연관 규칙의신뢰도 하한을 새롭게 정의해실제 드물게 관찰되는의미가 적은 연관규칙 제외너무 세분화한 품목을 갖고 연관성 규칙을 찾으면의미없는 분석이 됨
->적절히 구분되는큰 범주로 구분해전체 분석에 포함시킨 후 그 결과 중에서세부적으로 연관규칙을 찾는 작업 수행거래량이 적은 품목은 당연히 포함된거래수가 적을것이고,규칙 발견 시 제외하기 쉬움
-> 그품목이 관련성을 살펴보고자 하는중요한 품목이라면유사한 품목들과 함께 범주로 구성하는 방법 등을 통해 연관성 규칙의 과정에 포함
순차패턴(Sequence Analysis)
: 동시에 구매될 가능성이 큰 상품군을 찾아내는 연관성분석에 시간이라는 개념을 포함시켜 순차적으로 구매 가능성이 큰 상품군을 찾아내는 것
연관성분석에서의 데이터 형태에각각의 고객으로부터발생한 구매시점에 대한 정보가 포함
기존 연관성분석의 이슈
대용량 데이터에 대한연관성분석불가능시간이 많이 걸리거나기존 시스템에서 실행시시스템 다운되는 현상 발생
최근 연관성분석 동향
1세대 알고리즘 Apriori나2세대 FP-Growth에서 발전하여3세대 FPV를 이용해메모리를 효율적으로 사용함으로써 SKU레벨의 연관성분석을 성공적으로 적용- 거래내역에 포함되어있는
모든 품목의 개수가n개일 때,품목들의 전체집합(Item Set)에서추출할 수 있는품목 부분집합의개수는2^n-1(공집합 제외)개 Apriori: 모든 가능한 품목부분집합의개수를 줄이는 방식으로 작동하는 것FP-Growth:거래내역 안에 포함된품목의 개수를 줄여비교하는 횟수를 줄이는 방식으로 작동
Apriori 알고리즘
빈발항목집합(Frequent Item Set)
:최소 지지도보다큰 지지도 값을 갖는 품목의집합모든 품목집합에 대한 지지도를 전부 계산하는 것이 아니라,
최소 지지도 이상의빈발항목집합을 찾은 후 그것들에 대해서만연관규칙계산1994년에 발표된1세대 알고리즘구현과이해가 쉬움지지도가 낮은 후보 집합 생성시아이템의 개수가 많아지면서계산 복잡도가 증가한다는 문제점 존재
FP-Growth 알고리즘
후보 빈발항목집합을생성하지 않고,Fp-Tree(Frequent Pattern Tree)를 만든 후분할정복방식을 통해 Apriori 알고리즘보다더 빠르게빈발항목집합을추출Apriori의약점 보완을 위해 고안되어,
DB스캔 횟수가적고,빠른 속도로 분석 가능
*콘텐츠 기반 필터링(Content Based Filtering)
: 사용자가 특정 아이템을 선호하는 경우, 그 아이템과 비슷한 컨텐츠를 가진 다른 아이템을 추천해주는 방식
*협업 필터링(Collaborative Filtering)
: 많은 사용자들로부터 얻은 기호에 따라 사용자들의 관심사들을 자동적으로 예측하게 해주는 방법
연관성분석 활용방안
장바구니 분석:실시간 상품추천을 통한교차판매에 응용순차패턴 분석:A를 구매한 사람인데B를 구매하지 않은 경우,B를 추천하는교차판매 캠페인에 사용
연관성분석 예제
분석내용
Groceries데이터셋은 식료품 판매점의 1달 동안의 POS데이터- 총 169개의 제품, 9835건의 거래건수 포함
거래내역을inspect함수로 확인apriori함수로최소지지도와신뢰도는 각각0.01, 0.3으로 설정한뒤 연관규칙분석 실시
install.package("arules")
library(arules)
data(Groceries)
#1~3행
inspect(Groceries[1:3])
rules<-apriori(Groceries,parameter=list(support=0.01, confidence=0.3))
#상위 20개만 보여달라
inspect(sort(rules,by=c("lift"),decreasing=TRUE)[1:20])분석결과

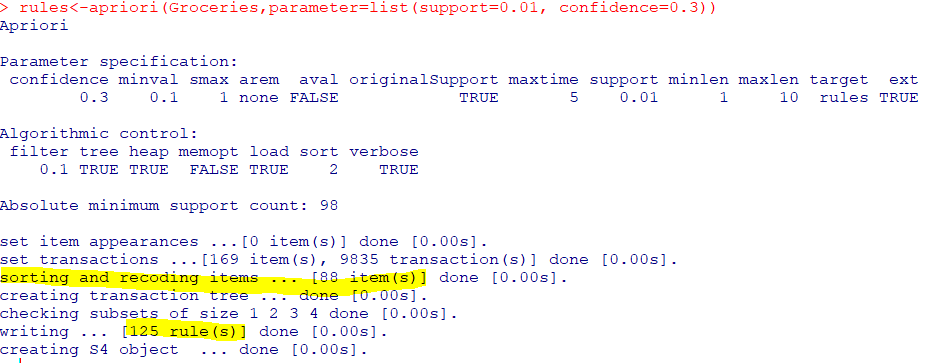
- 총
88개의 아이템으로연관규칙을 만들어냈으며,125개의 Rule 발견 규칙의 수가너무 적으면지지도와 신뢰도를 낮추고,너무 많으면지지도와 신뢰도를 높여야 함
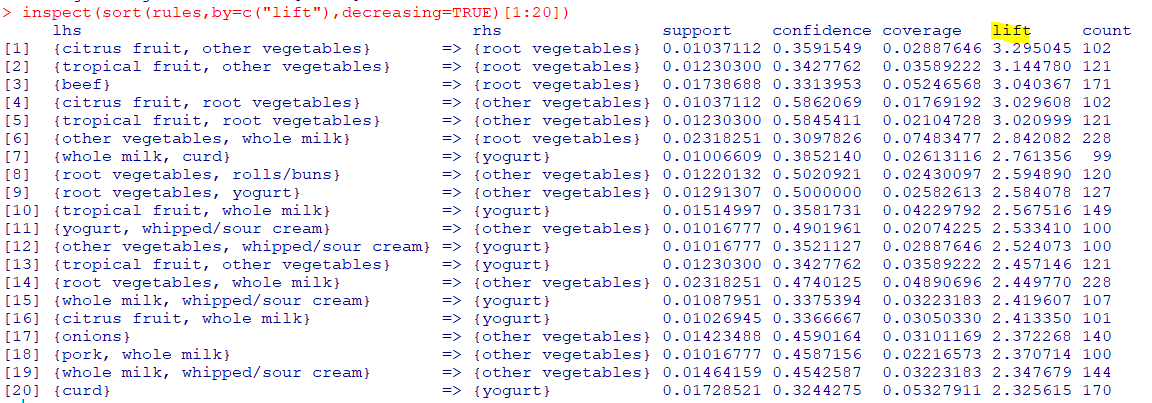
향상도를 기준으로내림차순 정렬한 후상위 5개의 규칙을 확인했을 때,rhs의 제품만 구매할 확률에 비해lhs의 제품을 샀을 때 rhs제품도 구매할 확률이약 3배가량 높음(Lift>3이므로)rhs와 lhs 제품들간결합상품 할인쿠폰혹은품목배치 변경등을 제안 가능
