📔설명
통계를 좀 더 깊숙히 파고들어보자!
🧂확률변수
이산형 확률변수
이산점(Discrete Points)에서0이 아닌 확률값을 가지는확률변수이산형 확률변수의확률
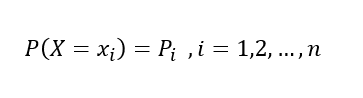
확률질량함수(Probability Mass Function, PMF)
: 각이산점에 있어서확률의 크기를 표현하는 함수- ex)
두 개의 주사위를 던지는 실험에서확률변수 X를'X=두 주사위 눈금의 합'이라고 정의한다면X의이산형 확률분포는 아래와 같음

이산형 확률변수의확률조건

연속형 확률변수
특정 실수 구간에서0이 아닌 확률을 갖는확률변수특정한 실수구간내에서0이 아닌 확률을 가지므로이 구간에 대한확률은함수의 형태로 표현확률밀도함수(Probability Density Function, PDF)
:연속형 확률변수 X의확률함수를f(x)라고 할 때,f(x)연속형 확률변수의확률조건

- ex)
확률변수 X가0과 1사이에서균등한 분포를 가진다면X의 확률밀도함수

누적 분포 함수(Cumulatvie Distribution Function, CDF)
-
특정 값 a에 대하여확률변수 X가X<=a인모든 경우의 확률의합
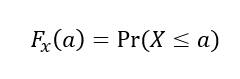
-
이산형 확률변수의 Fx(a)
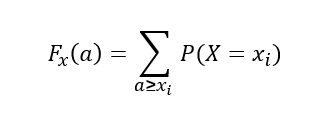
-
연속형 확률변수의 Fx(a)
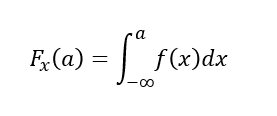
-
누적분포함수는증가함수이고,우측연속함수이며0과 1사이 값을 가짐 -
확률분포와의관계
:확률변수의누적분포함수는 그확률분포를유일하게 결정
구간(a,b]에 대한X의 확률은Pr(a<x<=b)=Fx(b)-Fx(a)
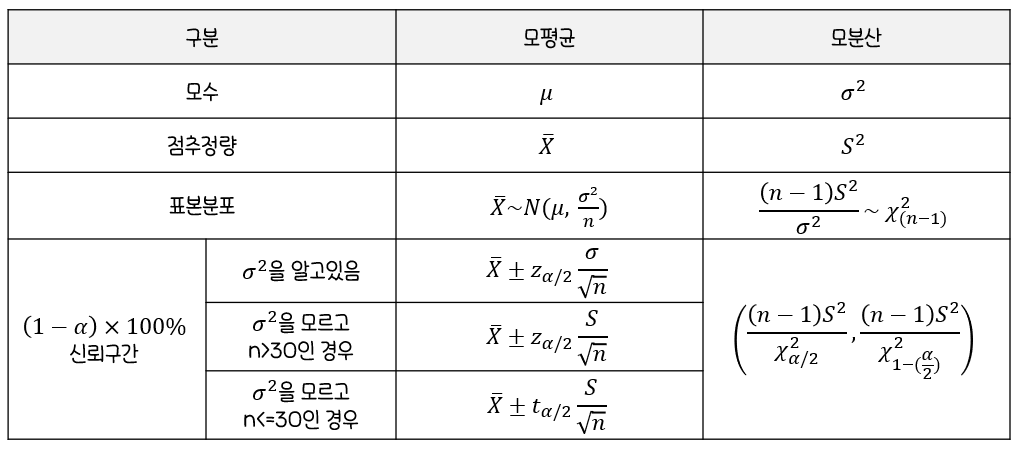
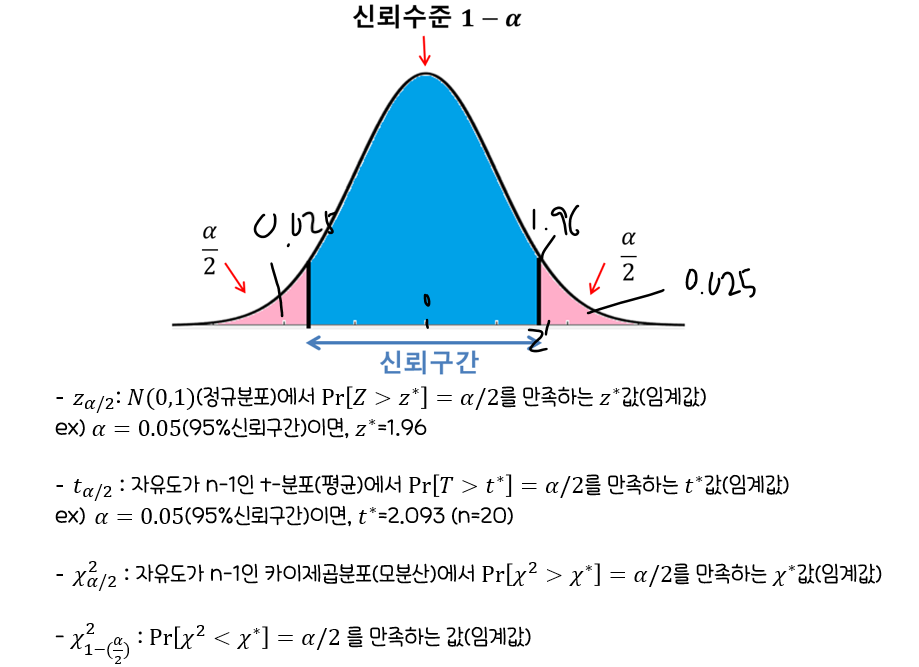
✨구간추정
모평균과 모분산에 따른 구간추정
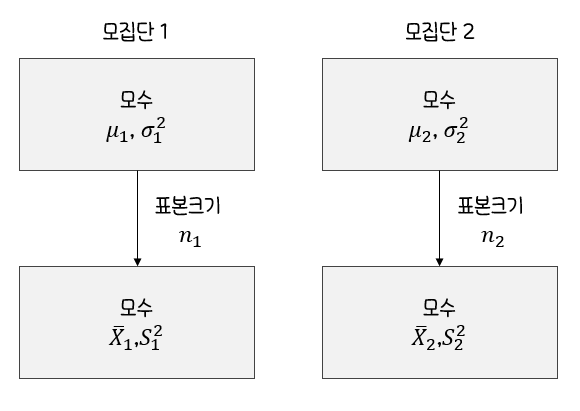
두 모평균 차이의 신뢰구간 추정(독립표본)
두 집단이서로 독립이라는 전제조건 하에두 모평균 차이에 대한 추정

두 모평균 차이의 신뢰구간 추정(대응표본)
투약 전후나이벤트 성과 비교와 같이짝을 이루는 각 쌍에 대한표본을 대상으로모평균의 차이 𝜇_1−𝜇_2에 대한 추정에는대응 표본(Pairwise Sample)사용
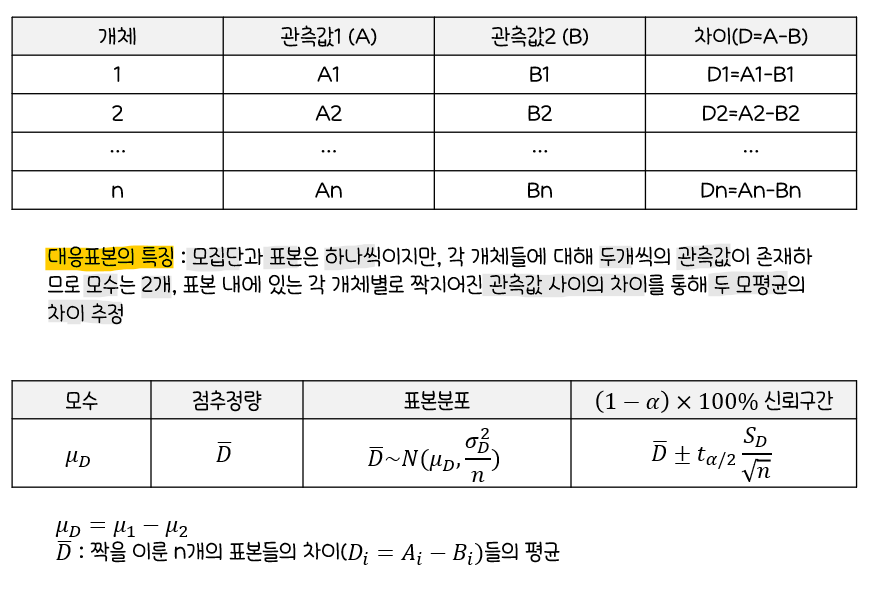
🎢중심극한정리(Central Limit Theorem)
-
중심극한정리(Central Limit Theorem, CLT)

-
자료가 관찰된
모집단의 분포가 실제로정규분포가 아닌경우에도중심극한정리에 의하여정규분포를 이용한추정량의 근사확률을 구할 수 있음
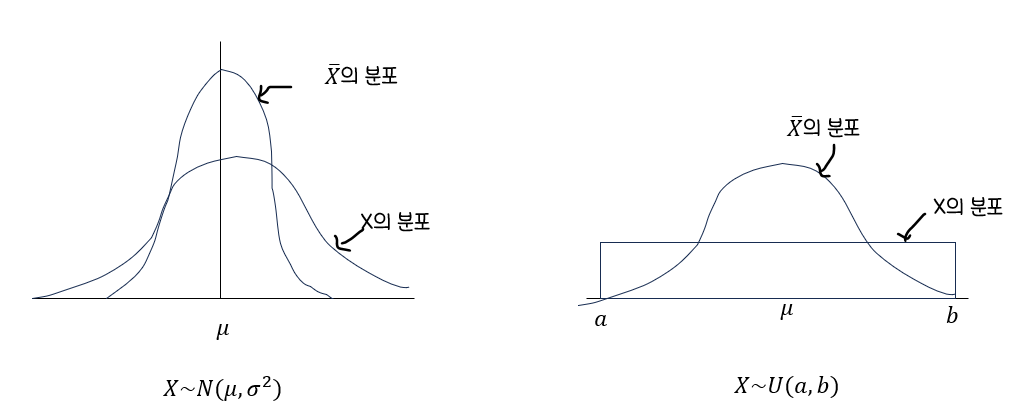
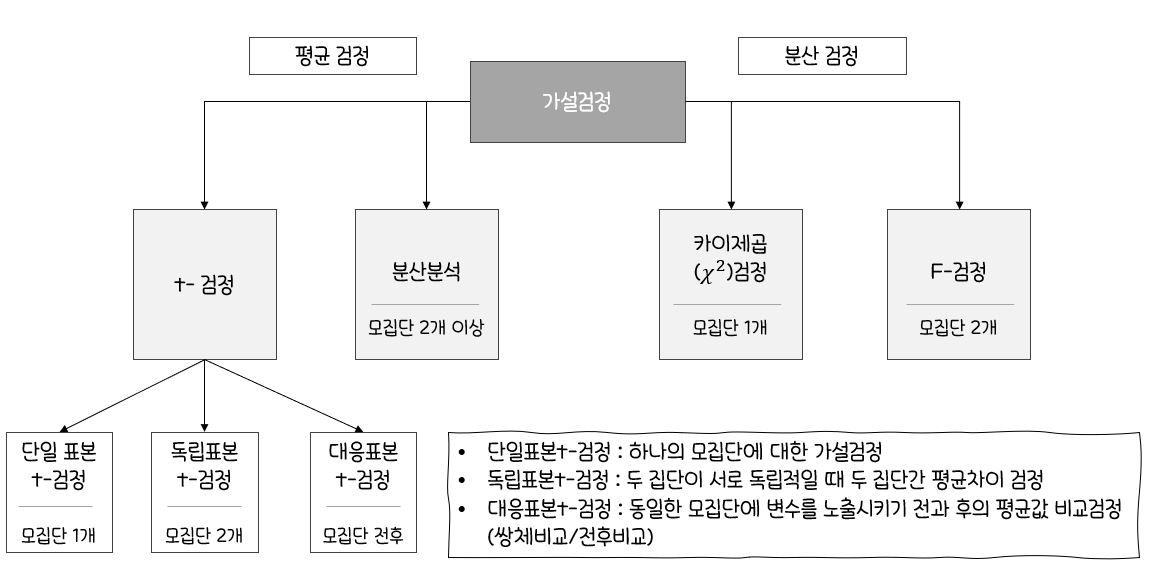
🎀가설검정
대립가설 H1과 기각역 C
검정통계량의 분포에서유의수준 α에 의해기각역 C의 크기가결정기각역의 위치는대립가설 H1의형태에 의해분포의 양쪽 끝(양측검정)또는한 쪽 끝(단측검정)으로 나뉨오른쪽 끝에 위치:오른쪽 단측검정왼쪽 끝으로 위치:왼쪽 단측검정귀무가설 H0가"모수가 특정값(μ0)이다"라고 할 때대립가설 H1
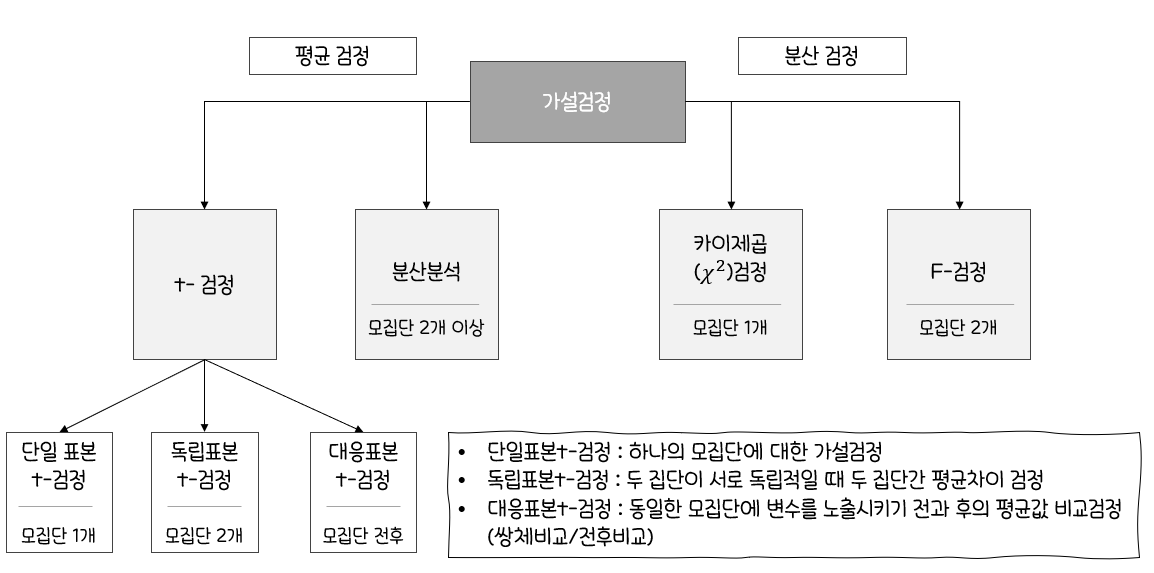
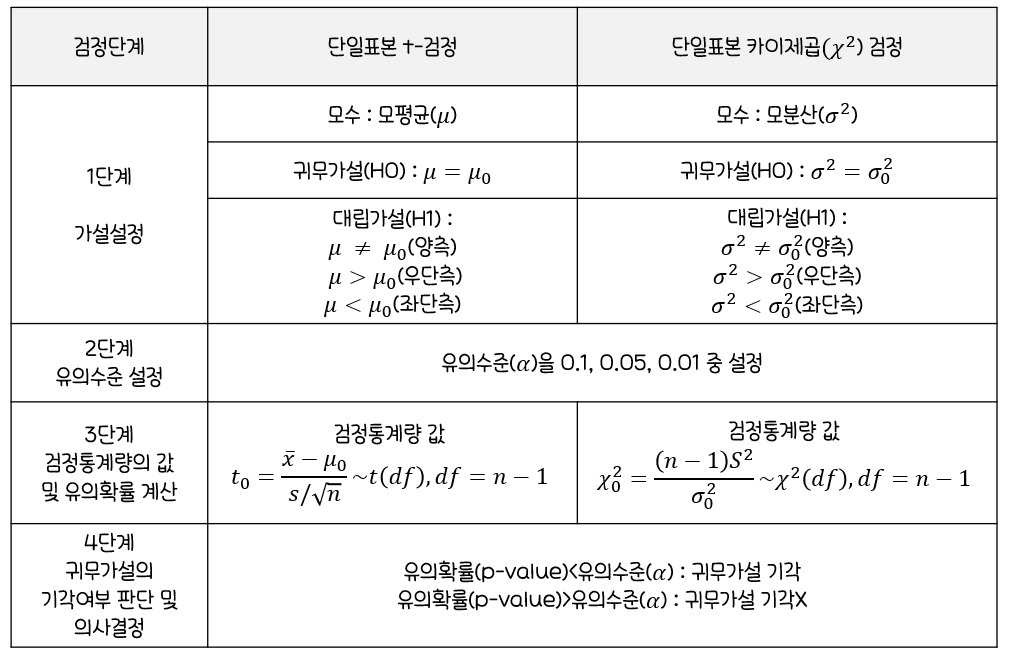
가설검정 단계
가설검정 단계
검정하고자 하는목적에 따라서귀무가설(H0)과대립가설(H1)을 설정검정통계량 T(X)를 구하고 그분포를 구함유의수준 α를 결정하고검정통계량 T(X)의 분포에서대립가설의 형태에 따라유의수준 α에 해당하는기각역C설정귀무가설(H0)이옳다는 전제 하에서표본관찰에 의한검정통계량 T(X)의 값을 구함T(X)의 값이기각역 C에 속하는가를 판단하여,기각역에 속하면귀무가설(H0)을 기각하고기각역에 속하지 않으면귀무가설(H0)을채택
*신뢰구간과 양측검정과의 관계
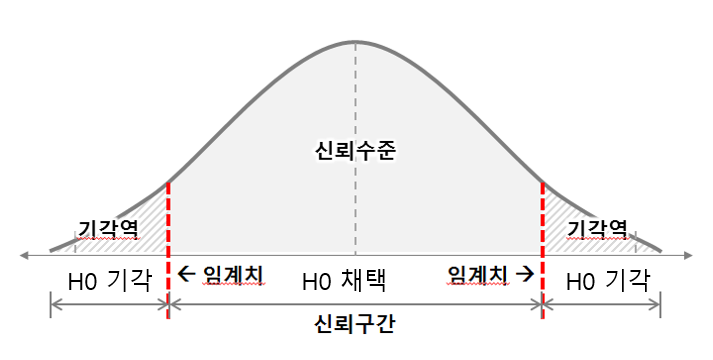
유의수준이α인양측 검정에서의귀무가설의 특정값(μ0)이(1-α)x100% 신뢰구간내에 포함된다면,귀무가설(H0) 채택- ex)
95% 신뢰구간이[49.50, 51.5]라고 가정,
해당신뢰구간이50을 포함하므로유의수준 5%에서대립가설(H1)"모평균이 50이 아니다.(μ!=50)(즉,μ0=50)"를채택
🍭상관계수
피어슨-스피어만 상관계수의 관계
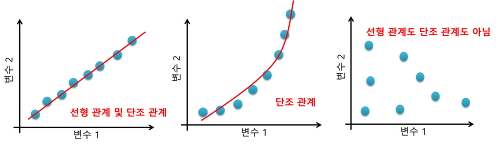
서열상관계수는 집단 내의개별 관측치를두 개의 서로 다른관점이나특성으로평가한순위값들을 이용해서 분석하는 경우에 사용단조함수(Monotonic Function)
:두 변수의순위 사이의의존성을 측정하는비모수 척도
->두 변수의 관계가 얼마나 잘설명될 수 있는지 판단
->순서관계 <=를보존하거나반전시키는 함수
->x<=y이면 f(x)<=f(y),x<=y 이면 f(x)>=f(y)스피어만 상관계수는 두 변수 사이의선형 관계를 평가하는피어슨 상관계수와 달리,선형 여부와 관계없이두 변수가단조적 관계가 있는지를 평가중복 데이터가 없다는 가정하에 각 변수가다른 변수의완벽한 단조 함수일 때+1또는 -1의관계발생- 두 변수 간의
스피어만 상관 계수= 두 변수의순위 값 사이의 피어슨 상관계수 - 두 변수 사이의
선형관계(피어슨)vs 두 변수 사이의단조적 관계(선형X)(스피어만)
🍱통계 분석 방법론
모집단의모수에 대해추정을 한 후에는모집단에 대해어떤 가설(Hypothesis)을 설정한 후 그 가설의타당성 여부검정한 집단,두 집단,독립적인 집단의평균부터분산검정 등에 대한통계 분석 방법론을 알아보자.
단일 모수의 가설검정 단계
두 모수의 가설검정 단계

🥂분산분석(Analysis of Variance, ANOVA)
t-검정:두 집단간의평균 차이비교하는 통계분석 방법분산분석:두 개 이상의다수 집단간평균을 비교하는 통계분석 방법독립변수(x)의 개수에 따라일원배치 분산분석,이원배치 분산분석,다원배치 분산분석으로 나뉨
일원배치 분산분석(One-Way ANOVA)
분산분석의 개념
두 개 이상의 집단에서그룹 평균 간 차이를그룹 내 변동에 비교하여 살펴보는 통계 분석 방법두 개 이상 집단들의평균 간 차이에 대한통계적 유의성을검증(두 개 이상의 집단들의 평균을 비교)하는 방법
일원배치 분산분석의 개념
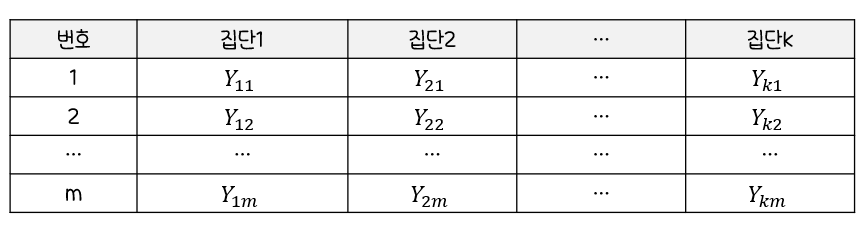
분산분석에서반응값에 대한하나의 범주형 변수의영향을 알아보기 위해 사용되는 검증 방법모집단의 수:제한X각 표본의 수: 같지 않아도 됨F-통계량(분산)이용- ex) 각 집단의
표본의 수가동일한 경우
(Yij는i번째 집단의j번째 관측값)
일원배치 분산분석의 가정
- 각 집단의
측정치는서로 독립적이며,정규분포를 따름 - 각 집단
측정치의분산은같다(등분산 가정)
분산분석표
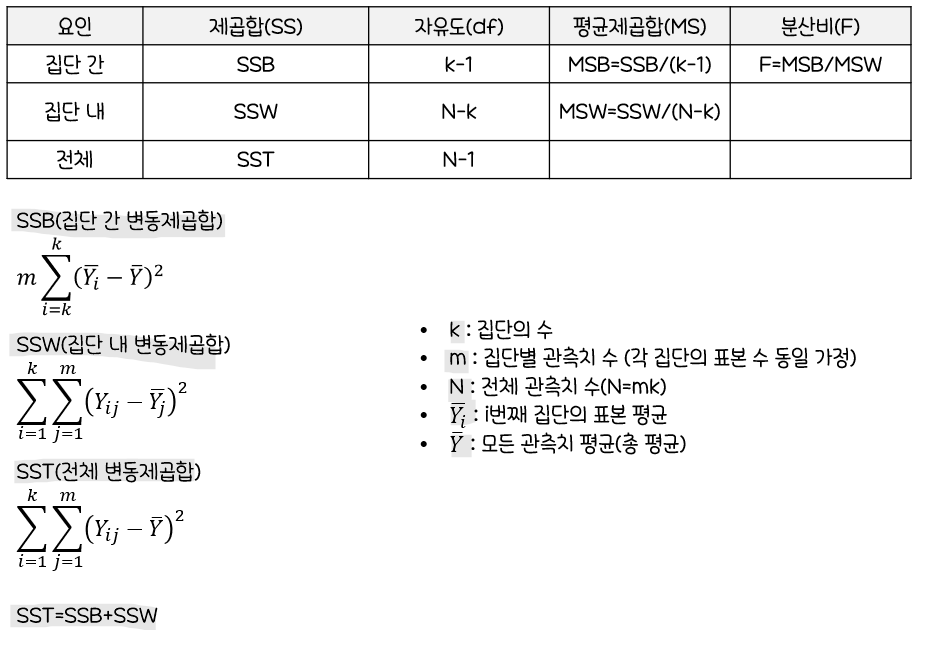
가설 검정
귀무가설(H0):k개의 집단 간모평균에는차이가 없다.(μ_1=μ_2=...=μ_k)대립가설(H1):k개의 집단 간모평균이모두 같다고 할 수 없다.
(H0 is not true)
사후 검정
분산분석의 결과귀무가설이 기각되어, 적어도한 집단에서 평균의 차이가 있음이통계적으로 증명되었을 경우,어떤 집단들에 대해서평균의 차이가 존재하는지를알아보기위해 실시하는 분석종류던칸(Duncan)의 MRT(Multiple Range Test)피셔(Fisher)의 최소유의차(LSD)튜키(Tukey)의 HSD방법Scheffe의 방법
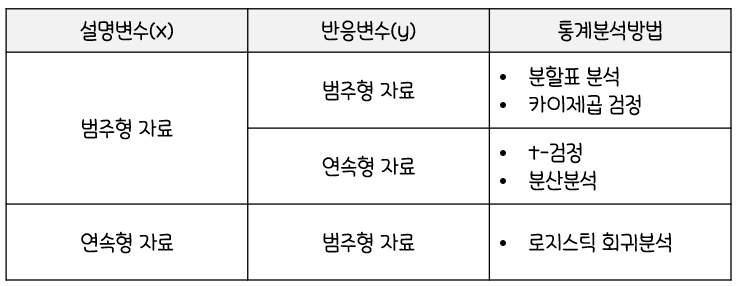
🌵범주형 자료 분석
- 분석에 사용되는 변수들이
범주형일 때 사용하는 분석 방법론 설명변수(x)와반응변수(y)에 따른 범주형 자료 분석 방법론분류
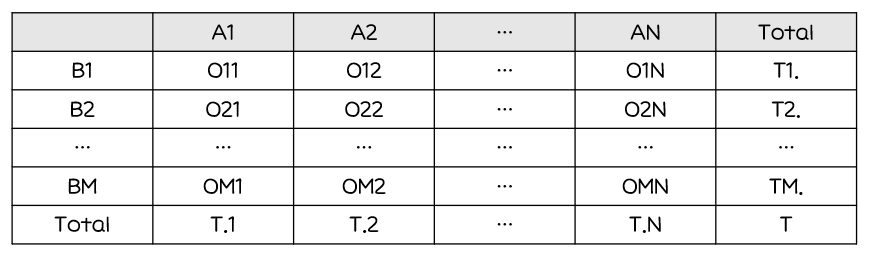
🪐분할표/교차표(Contingency Table) 분석
여러 개의범주형 변수를 기준으로빈도를표형태로 나타낸 것- ex)
2개의 범주형 변수(학년, 성적 등급)별빈도
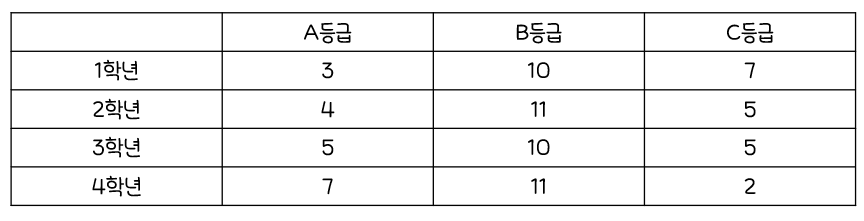
범주형 변수가1개:1원 분할표범주형 변수가2개:2원 분할표범주형 변수가3개 이상:다원 분할표분할표의 행:설명변수(x)분할표의 열:반응변수(y)범주형 자료를 분석시분할표를 기반으로 여러 가지 검정 수행
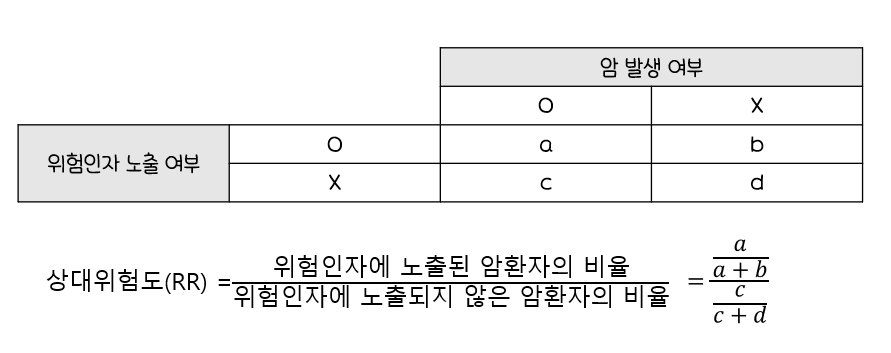
상대위험도(Relative Risk)
관심 집단의 위험률/비교 집단의 위험률위험률:특정 사건이발생할 비율- ex)
위험인자에 노출된 암환자의 확률/위험인자에 노출되지 않은 암환자의 확률 - 아래의
분할표에서상대위험도를 식으로 표현하면 아래와 같다.
🚲교차분석
교차표
두 변수의각 범주를교차하여데이터의 관측도수(빈도)를 표 형태로 나타냄
교차분석은교차표에서 각 셀의관찰빈도(자료로부터 얻은빈도분포)와기대빈도(두 변수가독립일 때이론적으로 기대할 수 있는빈도분포)간의차이검정
카이제곱검정
범주형 자료(명목/서열)인두 변수간의관계를 알아보기 위해 실시하는 분석 기법적합성 검정,독립성 검정,동질성 검정에 사용카이제곱(𝜒^2)으로검정 통계량을 이용
적합성 검정
- 실험에서 얻어진
관측값들이 예상한이론과일치하는지아닌지를 검정 관측값들이어떠한 이론적 분포를 따르고 있는지를 알아볼 수 있음.
->모집단 분포에 대한가정이옳게 됐는지를관측 자료와 비교하여 검정
독립성 검정
모집단이두 개의 변수 A, B에 의해범주화되었을 때, 이두 변수들 사이의관계가독립인지 아닌지검정모집단을범주화하는 기준이 되는 두 변수A, B가서로 독립적으로관측값에 영향을 미치는지 여부 검정검정 통계량 값을 계산시교차표활용
동질성 검정
모집단이임의의 변수에 따라R개의 속성으로범주화되었을 때,R개의부분 모집단에서 추출한 각표본인C개의 범주화된 집단의 분포가 서로동일한지를 검정검정 통계량 값을 계산할 때는교차표활용계산법,검증법은 모두독립성 검정과 같은 방법

👨🏻더빈 왓슨(Durbin-Watson) 검정
회귀분석의 주요한 가정 중오차항이독립성을 만족(독립성)하는지 검정하기 위해서 사용- 검정 결과
더빈 왓슨 통계량이2에 가까울 수록오차항의 자기상관이 없음 더빈 왓슨 통계량이0에 가까울수록양의 상관관계더빈 왓슨 통계량이4에 가까울수록음의 상관관계- 즉 ,
더빈 왓슨 통계량이0혹은 4에 가까울 수록잔차들 간의 상관관계가 있어서회귀식 부적합
🧀정규화 선형회귀(Regularized Linear Regression)
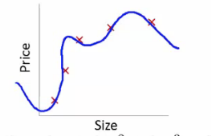
선형회귀 계수에 대한제약 조건을 추가하여모델이 과도하게 최적화되는 현상(과적합, Overfitting)을 막는 방법- 아래 그래프는 모델이
학습 데이터를 매우잘 적합하고 있으나,미래 데이터가조금만 바뀌어도예측값이과도하게 변함
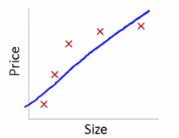
- 아래 그래프는
정규화를 수행하여학습데이터에 대한설명력은 조금포기하는 대신미래 데이터의 변화에 대해상대적으로 안정된 결과
모형이과적합되면계수의 크기도 과도하게증가
->정규화 선형회귀에서는계수의 크기를제한하는 방법으로제약조건추가정규화 선형회귀에서는제약조건의종류에 따라Ridge회귀,Lasso회귀,ElasticNet회귀가 사용됨
릿지(Ridge)회귀
가중치들의 제곱합(Squared Sum of Weights)을최소화하는 것을제약조건능형 회귀모형이라고도 함
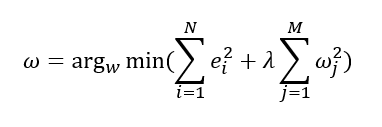
가중치의모든 원소가0에 가까워지는 것을 원함
-> 이를 위해 회귀 모델에 사용하는규제 방식을L2 규제(Penalty)𝜆: 기존의잔차 제곱합과 추가적인제약조건의 비중을조절하기 위한초매개변수(Hyper Parameter)𝜆가 커짐:가중치의 값들이작아지며,정규화 정도가 커짐𝜆가 작아짐:정규화 정도가 작아짐𝜆=0:일반적인 선형회귀모형
라쏘(Lasso)회귀
라쏘(Least Absoulte Shrinkage and Selection Operator, Lasso)회귀모형
:가중치 절대값의합을최소화하는 것을 제약조건절대값의 크기가 클 수록 penalty 부여릿지회귀에서는가중치가0에 가까워질 뿐,실제로 0이 되지는 않음라쏘회귀에서중요하지 않은 가중치는0이 될 수 있음
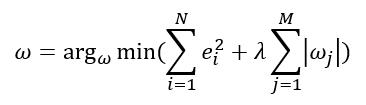
라쏘회귀에서 사용하는규제 방식을L1 규제(Penalty)
엘라스틱넷(Elastic Net)
릿지회귀+라쏘회귀
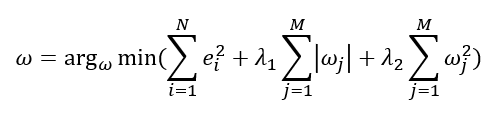
가중치 절댓값의 합과제곱합을 동시에제약조건으로 가지는 모형𝜆_1와𝜆_2라는두 개의 초매개변수가짐
🍮회귀분석의 영향력 진단
영향력 진단:적합된 회귀모형의안전성평가자료에서특정 관측치가제외됨에 따라분석 결과의 주요 부분에많은 변동=>안전성 약함영향점:선형회귀분석에서회귀직선의 기울기에영향을 크게 주는 점영향력 진단의 방법:Leverage H,Cook's Distance,DFBETAS,DFFITS등
Leverage H(지레점, 레버리지)
레버리지:𝐻=𝑋(𝑋^𝑇 𝑋)^(−1) 𝑋^𝑇(Hat Matrix)의i번째대각원소로관측치가다른 관측치 집단으로부터떨어진 정도2 x (p+1)/n보다크면영향치이거나이상치
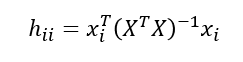
Cook's Distance(쿡의 거리)
Full Model에서i번째 관측치를 포함하여계산한 적합치와i번째 관측치를 포함하지 않고계산한적합치 사이의 거리기준값인1보다 클 경우에영향치

DFBETAS(Difference in Betas)
DFBETAS의절대값이커지면i번째 관측치가영향치혹은이상치기준값은2나2/√n(표본을 고려한 경우)사용DFBETAS값이기준값보다클 경우영향치
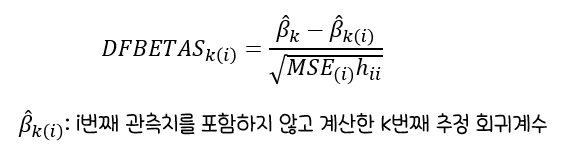
DFFITS(Difference in Fits)
i번째 관측치 제외시종속변수 예측치의변화정도를 측정한 값DFFITS의절대값이기준값인2x(p+1)/n보다클수록영향치
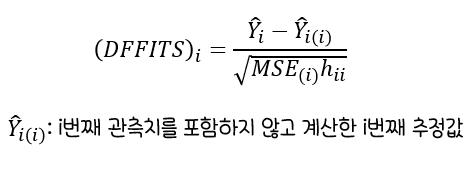
🥛변수 선택의 기준으로 사용되는 통계량
수정된 결정계수(Adjusted R Square, R^2_a)
설명변수(x)의 개수가증가하면결정계수도 함께증가
->수정된 결정계수를 이용해 단점 보완,변수 선택수정된 결정계수:변수의 개수가증가함에 따라처음에는 감소하다가점점 안정화되고나중에는 약간 증가하는 경향
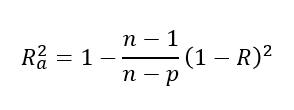
수정된 결정계수를 이용하여변수 선택시MSE값이최소인 시점의 모형을 선택하거나이 값의 최소와 비슷해서더 이상 변수를 추가할 필요가 없는 시점의 모형 선택
*모수 절약의 원칙(Principle of Parsimony)
: 회귀모형을 구축할 때 가능한 작은 수의 독립변수를 이용해야 하는 통계학의 원칙 -> 모형의 간명성
Mallows'Cp
Mallow가 제안한 통계량Cp값은최소자승법(최소제곱법)을 사용해 추정된회귀모형의적합성을 평가하는데 사용

Cp값이작고,p+상수(변수의 개수+상수)에가까운모형 선택
| Cp값 | 해석 |
|---|---|
| Cp값이 p(변수의 개수)와 비슷한 경우 | Bias(편향)이 작고 우수한 모델 |
| Cp값이 p보다 큰 경우 | Bias가 크고 추가적인 변수가 필요한 모델 |
| Cp값이 p보다 작은 경우 | Variance(분산)의 증가폭보다 Bias의 감소폭이 더 크며, 필요 없는 변수가 모델에 있다는 것을 의미 |
🧪실험계획법(Design Of Experiment, DOE)
실험 계획법의 개념
시스템이나프로세스의결과에영향을 미치는인자를 도출하고,측정 데이터를통계적으로 분석하기 위한실험을 설계하는 방법실험 방식,데이터 수집 방법,활용 통계 기법등 실험의 모든 과정 설계최소 실험 횟수로최대의 정보를 얻는 것을 목적
계획 설계의 목적
분산분석및검정과추정의 문제:어떠한 요인이특성치 변화에유의미한 영향을 주는지, 또한해당 요인의영향이어느 정도인지 파악최적 반응 조건의결정 문제:어떤 인자를 사용해야가장 원하는 결과값을 얻을 수 있는지를 파악오차항 추정의 문제: 이해하기 어렵던오차와 그변동에 관한 정도 파악
실험계획 원리
랜덤화의 원리(Randomization)
:실험 순서를무작위로 선택반복의 원리(Replication)
:인자의 동일수준 내에서최소 두 번 이상실험 진행블록화의 원리(Blocking)
:실험 전체를시간적/공간적으로분할하여 블록으로 만듦직교화의 원리(Orthogonality)
:요인간직교성을 갖도록 실험을 계획교락의 원리(Confounding)
:고차항의교호효과와블록효과를교락시키는 방법
*교호효과 : 한 요인의 효과가 다른 요인의 수준에 의존하는 경우
*교락 : 실험 수를 줄이는 대신 얻을 수 있는 정보는 좀 손해를 봄
주요 용어
인자(Factor): 실제실험대상.입력변수 X특성치(Characteristic Value): 실험의 모든결과값.출력변수 Y수준(Level): 실험하기 위한인자의 조건. 인자의정도나값주효과(Main Effect): 각입력변수의수준 간 차이.
인자가독립적으로반응에 미치는 영향교호효과(Interaction Effect):특정한 인자 수준의조합에서 일어나는 효과.
인자들이 혼합되어 반응에 미치는 영향교락(Confounding):2개 이상의 효과(주효과 or 교호효과)를구별할 수 없도록계획적으로조합하는 것블록(Block):실험 단위가균일할 수 있도록 단위를 모은 것반복(Replication): 인자들의동일한 수준 조합에서다회의 실험을 진행중복(Repetition):한 실험에서여러 개의 대상을 측정
실험 계획법의 종류
요인배치법(Factorial Design)
모든 인자간의수준 조합에서 실험이 이루어지는완전랜덤화방법교호효과를 포함한 모든요인효과를추정가능K^n형 요인실험:인자 수가n, 각 인자의수준 수가k인실험계획법
분할법(Split-Plot Design)
완전랜덤화하기 힘들 경우,몇 단계로 분할하여각 단계별로완전 랜덤하게실험 순서를 결정랜덤화가 가장 어려운 것을1차 단위로,비교적 쉬운 것을후 단위로 배치
교락법(Confounding Method)
- 검출할 필요가 없는
교호작용을다른 요인과교락하도록배치 실험 횟수를 늘리지 않고실험 전체를몇 개의 블록으로 나누어배치동일 환경에서의실험 횟수를줄일 수 있음고차의 교호작용을블록에 교락시키기 때문에주효과가높게 추정
난괴법(Randomized Block Design, RBD, 랜덤화 블록 실험설계)
실험 단위를 몇 개의반복으로 나누어 배치A가모수인자이고,B가변량인자일 때,A인자의 수준 수가1이고,B인자의 수준 수가m인반복이 없는이원배치 분산분석방법실험 오차를줄일 수 있기 때문에효율이 높고비교적분석이간단
*모수인자 : 인자의 수준을 지정하는 것이 기술적으로 의미 O
*변량인자 : 인자의 수준을 지정하는 것이 기술적으로 의미 X