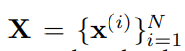Auto-Encoding Variational Bayes

먕먕·2023년 5월 18일

0. Abstract

stochastic variational 추론 및 학습 알고리즘을 소개한다.

Variational lower bound 의 reparametrization 을 통해 SGVB라는 새로운 estimator를 제안하였고, 이를 이용해 AEVB라는 최적화 알고리즘을 제안한다.
AEVB 알고리즘은 데이터 포인트마다 연속적인 잠재 변수를 갖는 i.i.d. 데이터 셋에서, intractable했던 사후추론을 fitting하여 효과적으로 수행할 수 있다.

1. Introduction

variational bayesian(VB) 접근은 intractable한 사후확률에 근사하는 최적화를 포함한다. 가변 하한의 재매개화를 통해 단순하고 미분 가능한 하한 추정기인 Stochastic Gradient Variational Bayes(SGVB)를 얻고 SGVB를 통해 연속적인 잠재 변수를 가진 모델에 대한 효율적인 근사 사후 추론을 할 수 있다. 또한 standard stochastic gradient를 통해 쉽게 최적화 가능하다.

연속적인 잠재변수를 갖는 i.i.d. 데이터 셋의 경우 AutoEncoding VB(AEVB)를 사용할 수 있다. AEVB는 SGVB 추정기를 사용해 효율적인 근사적 사후 추론과 모델 매개 변수의 효율적인 학습을 가능하게 한다. 학습된 근사 사후 추론 모델은 recognition, denoising, representation, visualization에 활용될 수 있다.

2. Method

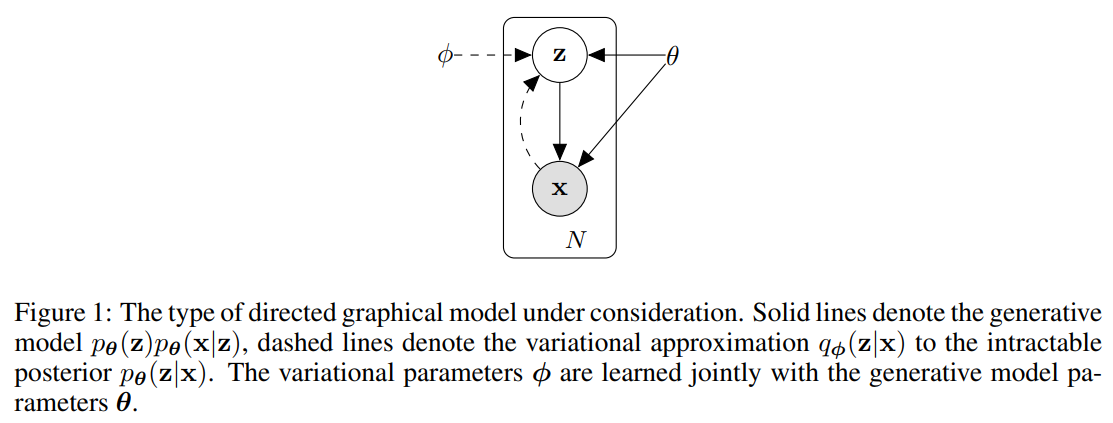
연속적인 잠재 변수를 갖는 다양한 graphical 모델에 대한 lower bound estimator를 유도하는 전략에 대해 설명한다. 데이터 포인트마다 잠재변수가 있는 i.i.d. 데이터 셋이라고 제약을 걸고, 전역 파라미터에 ML(maximum likelihood)나 MAP(maximum posteriori) 추론을 수행하고 잠재 변수에는 variational 추론을 하려고 한다. 또한 단순성을 위해 static(fixed) 데이터 셋을 가정한다.

2.1 Problem scenario

N개의 i.i.d. 샘플로 구성된 데이터 셋을 고려한다

z : 관측되지 않은 연속 랜덤 변수 z
x : z를 포함하는 어떠한 랜덤 프로세스에 의해 생성

x를 생성하는 과정은 크게 두 가지로 나뉘는데,

z(i)는 사전분포 pθ∗(z)에 의해 생성되고,
x(i)는 조건부확률 pθ∗(x|z)에 의해 생성된다

θ와 z에 대해서 거의 모든 곳에서 미분 가능함을 가정한다. 실제 parameter의 값 θ*와 random variable z(i)는 그 값을 직접적으로 알 수가 없다.

또한 marginal likelihood와 사후 확률에 대한 단순화 가정을 하지 않는다. 아래와 같은 경우에도 잘 작동하는 알고리즘에 관심이 있다.

Intractability : marginal 우도의 적분 pθ(x) = ∫ pθ(z)pθ(x|z)dz, 사후 밀도 pθ(z|x) = pθ(x|z)pθ(z)/pθ(x), mean-field VB 알고리즘에 대한 적분이 해결하기 어려운 경우.
large dataset : 데이터가 너무 많아서 배치 최적화가 너무 비용이 많이 드는 경우. 작은 minibatch나 단일 데이터 포인트를 사용하여 매개 변수를 업데이트하고자한다.

위 시나리오에서 세 가지 문제점에 관심을 갖고, 이에 대한 해결책을 제시한다.

파라미터 θ에 대한 효율적인 근사 ML, MAP 추정. 매개 변수 자체에 관심을 갖는 것이며 이러한 파라미터 를 사용하여 숨겨진 무작위 과정을 모방하고 실제 데이터와 유사한 가상 데이터를 생성할 수 있다.
파라미터 θ의 선택에 따라 관측값 x가 주어졌을 때 잠재 변수 z에 대한 효율적인 근사적인 사후 추론. 데이터 표현화에 유용하다.
변수 x의 효율적인 근사 marginal 추론. x에 대한 사전 분포가 필요한 모든 추론 작업을 수행할 수 있다. image denoising, inpainting and super-resolution에 유용하다.

qø(z|x) recognition model/probabilistic encoder: 추론하기 어려운 실제 사후 분포 pθ(z|x)의 근사치

인식 모델 매개변수 ø를 생성 모델의 매개변수 θ와 함께 학습시킨다.
데이터 포인트 x가 주어지면 데이터 포인트 x가 생성될 수 있는 코드 z의 가능한 값들에 대한 분포 (예: 가우시안)를 생성 → 확률적 인코더
pθ(x|z)는 z가 주어지면 해당하는 x의 가능한 값들에 대한 분포를 생성하는 확률적 디코더

2.2 The variational bound

marginal likelihood는 개별 데이터 포인트의 marginal likelihood의 합으로 구성된

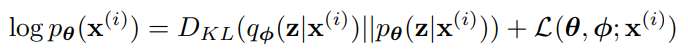
우변의 첫 항은 사후 분포로부터의 근사의 KL divergence이다. KL-divergence가 음수가 아니므로, 우변의 두번째 항인 L(θ, ø; x(i))는 데이터 포인트 i의 marginal likelihood에 대한 variational lower bound라고 불리며 다음과 같이 쓸 수 있다.

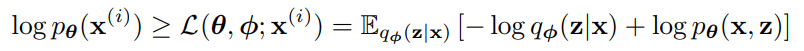
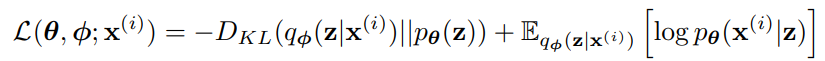
lower bound L(θ, ø; x(i))을 variational 파라미터 ø와 생성 파라미터 θ에 대해 미분하고 최적화하려고 할 때, ø에 대한 gradient를 일반적인 Monte Carlo gradient estimator를 사용해 구하면 높은 분산 값을 갖고 이는 실용적이지 못하다.

2.3 The SGVB estimator and AEVB algorithm

lower bound의 실용적인 estimator와 파라미터에 대한 미분에 대해 소개한다. 근사 사후분포를 qø(z|x)로 표기한다.

선택된 근사 사후 확률 qø(z|x)에 대해 2.4장에서 설명할 일부 조건하의 상황에서, 노이즈 변수 ϵ의 미분 가능한 변환인 gø(ϵ,x)를 사용해 랜덤 변수 z~ ∼ qø(z|x)를 재매개화 할 수 있다.

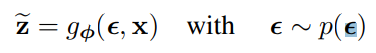
qø(z|x)에 대한 함수 f(z)의 기대값에 대한 Monte Carlo 추정을 할 수 있다

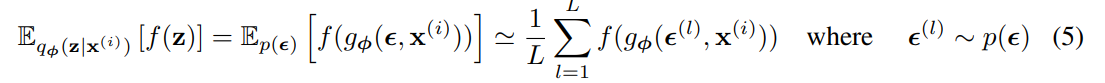
위 기법을 variational lower bound에 적용하여 generic Stochastic Gradient Variational Bayes (SGVB) 추정기를 얻을 수 있다

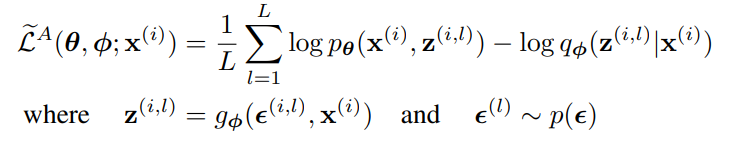
KL-divergence는 분석적으로 적분될 수 있기에 재구성 오차 Eqø(z|x)[logpθ(x(i)|z)]는 샘플링을 통한 추정을 필요로 한다. KL-divergence는 ø를 regularizing하여 근사 사후분포가 사전분포 pθ(z)에 가까워지도록 유도하는 것으로 해석할 수 있다. 따라서 일반적인 estimator보다 분산이 적은 두번째 SGVB estimator가 생성된

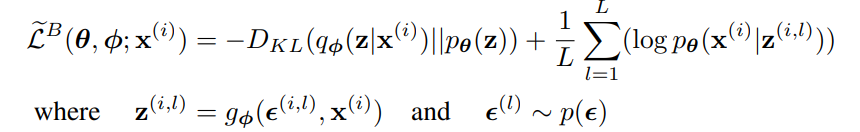
N개의 데이터 포인트를 가진 데이터셋 X에서 여러 개의 데이터 포인트를 사용하여 미니배치를 구성한 경우, 전체 데이터셋의 marginal likelihood lower bound estimator를 만들수 있다.

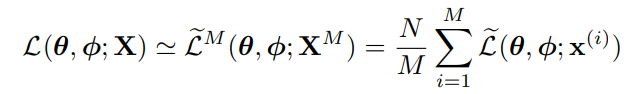
미니배치는 N개의 데이터 포인트를 가진 전체 데이터셋 X에서 M개의 데이터 포인트를 무작위로 추출한 샘플이다. 미니배치 크기 M이 충분히 크다면 데이터 포인트 당 샘플 수 L을 1로 설정할 수 있음을 발견했다. derivates를 구할 수 있으며 구한 gradient는 SGD나 Adagrad와 같은 확률적 최적화 방법과 함께 사용할 수 있다.

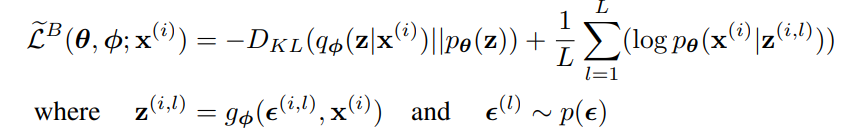
이 식에서 주어진 목적 함수를 보면 오토인코더와의 관련성이 명확하다. 첫 항은 (KL-divergence) regularizer 역할을 하며 두번째 항은 expected negative reconstruction error이다. gø는 데이터 포인트 x(i)와 무작위 노이즈 벡터 ϵ(i)를 사용해 데이터 포인트의 근사 사후 분포에서 샘플을 생성하는 방법으로 선택된다. 샘플 z^(i,l)은 logpθ(x(i)|z(i,l))의 입력이 되고 이는 z가 주어졌을 때 생성 모델에 따른 데이터 포인트 x(i)의 확률 밀도와 같다. 이 항이 오토인코더에서의 음의 재구성 오차이다.

2.4 The reparameterization trick

qø(z|x)에서 샘플을 생성하기 위한 방법을 설명한다. 연속적인 랜덤 변수 z와 조건부 분포 z ~ qø(z|x)가 주어지는 경우, z를 determinisitc 변수인 z = gø(ϵ,x)로 표현할 수 있다. ϵ는 독립적인 marginal p(ϵ)를 갖는 보조 변수이며 gø는 ø로 매개화된 백터 함수이다.

재매개 변수화를 사용하여 qø(z|x)에 대해 기댓값을 다시 쓸 수 있으므로 기댓값의 Monte Carlo 추정치가 ø에 대해 미분 가능하다.

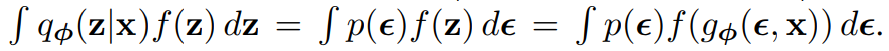
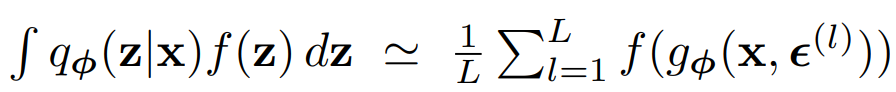
이 기법을 적용해 variational lower bound의 미분 가능한 estimator를 얻는다

예를 들어 단변량 가우시안의 경우

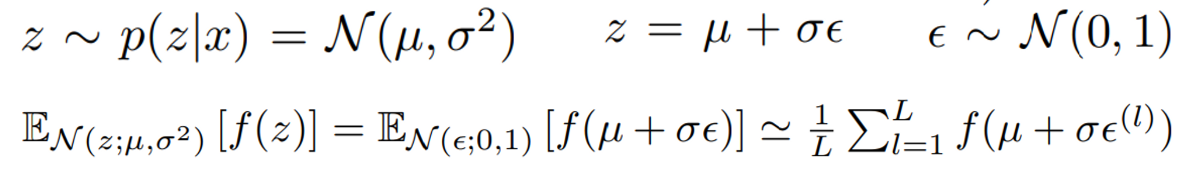
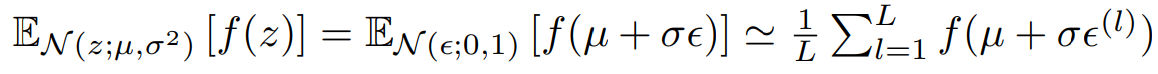
위 접근법을 통해 다음과 같은 qø(z|x)에 대해 미분 가능한 변환 gø와 보조 변수 ϵ ~ p(ϵ)를 선택할 수 있다.

tractable inverse CDF : ϵ ~ U(0, I), gø(ϵ, x)는 qø(z|x)의 inverse CDF. (Examples: Exponential, Cauchy, Logistic, Rayleigh, Pareto, Weibull, Reciprocal, Gompertz, Gumbel and Erlang distributions.)
가우시안 예시와 유사하게 ‘위치-스케일’ 분포 계열의 경우 ϵ로 표준 분포(location = 0, scale = 1)을 선택하고 g = location + scale * ϵ. (Examples: Laplace, Elliptical, Student’s t, Logistic, Uniform, Triangular and Gaussian distributions.)
Composition : 랜덤 변수를 보조 변수의 다른 변환으로 표현할 수 있다. ( Examples: Log-Normal (exponentiation of normally distributed variable), Gamma (a sum over exponentially distributed variables), Dirichlet (weighted sum of Gamma variates), Beta, Chi-Squared, and F distributions.)

3. Example : Variational Auto-Encoder

확률적 인코더 qø(z|x) (= 생성 모델 pθ(x, z)의 사후 확률에 대한 근사치)로 신경망을 사용하는 예제를 보자. 이때 매개변수 ø와 θ가 AEVB 알고리즘으로 동시에 최적화된다.

잠재변수에 대한 사전 분포를 pθ(z) = N (z; 0, I)로 둔다. 사전 분포에는 매개변수가 없다. pθ(x}z)를 다변량 가우시안 또는 베르누이로 설정하고, 분포 파라미터는 MLP를 사용하여 z에서 계산한다. 이 경우 실제 사후확률 pθ(z|x)는 intractable하다. qø(z|x) 형태에는 많은 자유도가 있지만, 실제 사후확률이 대략적으로 approximately diagonal covariance한 가우시한 형태로 가정한다. 이 경우 variational approximate posterior가 diagonal covariance 구조의 다변량 가우시안이라고 설정할 수 있다.

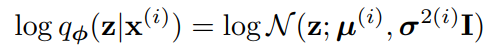
근사 사후확률의 평균이 µ(i), 표준편차가 σ(i)이며 인코딩 MLP의 출력은 데이터 포인트 x(i)와 variational parameter ø의 비선형적 함수이다.

사후확률 z(i,l) ~ qø(z|x(i)를 z(i,l) = gø(x(i), ϵ(l)) = µ(i)+σ(i) ⊙ ϵ(l)을 사용하여 샘플링한다. ⊙는 element-wise product이다. 이 모델에서 사전확률 pθ(z)와 qø(z|x)는 가우시안 분포이다. 이 경우 KL-divergence가 estimation 없이 미분 가능하다. 이 모델과 데이터 포인트 x(i)에 대한 estimator는 다음과 같다

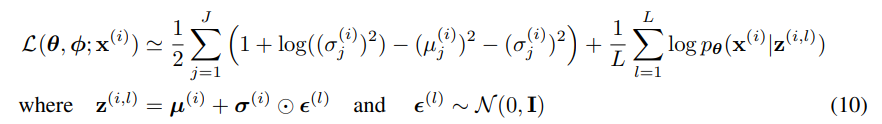
디코딩 항인 logpθ(x(i)|z(i,l))은 베르누이 또는 가우시안 MLP이다.

4. Experiments

MNIST와 Frey Face 데이터셋에서 이미지의 생성 모델을 학습하고, AEVB와 wake-sleep 알고리즘의 성능을 비교한다. 두 알고리즘은 동일한 인코더와 변분 오토인코더를 사용하며, 매개 변수는 확률적 그래디언트 상승을 통해 최적화되었다. 결과적으로 변분 하한과 추정 주변 우도를 평가하여 AEVB가 wake-sleep 알고리즘과 비교하여 어떤 성능을 보이는지 알아보았다

Likelihood lower bound
MNIST 데이터셋에는 500개의 은닉 유닛을 가진 생성 모델 및 인코더, Frey Face 데이터셋에는 200개의 은닉 유닛을 가진 생성 모델 및 인코더를 훈련시켰다. 실험 결과, 불필요한 잠재 변수가 과적합을 유발하지 않았으며, 이는 변분적 경계의 정규화 특성으로 설명된다.

Marginal likelihood
저차원의 잠재 공간에서는 MCMC 추정기를 사용하여 학습된 생성 모델의 주변 우도를 추정할 수 있다. 인코더와 디코더에는 다시 100개의 은닉 유닛과 3개의 잠재 변수를 가진 신경망을 사용했으며, 잠재 공간의 차원이 높아질수록 추정치가 신뢰할 수 없어졌다.

visualisation of high-dimensional data
저차원의 잠재 공간 (2D)을 선택한다면, 학습된 인코더 (인식 모델)를 사용하여 고차원 데이터를 저차원의 매니폴드로 투영할 수 있다.

5. Conclusion

연속 잠재 변수를 가진 효율적인 근사 추론을 위한 추정기인 Stochastic Gradient VB (SGVB)를 소개했다. 제안된 추정기는 표준 확률적 그래디언트 방법을 사용하여 직관적으로 미분 가능하고 최적화할 수 있다. i.i.d. 데이터셋과 각 데이터 포인트마다 연속적인 잠재 변수의 경우, 효율적인 추론과 학습을 위한 Auto-Encoding VB (AEVB)라는 알고리즘을 소개했다. 이 알고리즘은 SGVB 추정기를 사용하여 근사 추론 모델을 학습다.