CMAPSS EDA #1
NASA의 TurboFan 데이터 세트 탐색
탐색적 데이터 분석 및 기준선 선형 회귀 분석 모델
- 동일한 문제에 서로 다른 적절한 기술을 적용하는 방법에 대한 완벽한 개요를 파악하지 못함
- 첫 번째 데이터 세트에만 초점을 맞추고, 더 복잡한 문제가 어떻게 해결될 수 있는지 추측
여러 분석 기법을 소개하고 설명하는 동시에 더 복잡한 데이터 세트를 위한 솔루션을 제공
Exploratory Data Analysis
엔진은 초기에는 정상적으로 작동하지만 시간이 지남에 따라 고장이 발생g한다. 교육용 세트의 경우, 엔진은 고장 시까지 작동하며, 테스트에서는 고장 전에 시계열 종료를 'sometime'으로 설정한다. 목표는 각 터보팬 엔진의 남은 수명(RUL)을 예측하는 것
어떤 도메인 지식도 사용할 수 없다. 센서가 무엇을 측정했는지 모르기 때문.
모든 엔진이 동일한 장애를 발생시키고 하나의 작동 조건만 갖는 첫 번째 데이터 세트(FD001)를 탐색하는 데 초점을 맞출 것이다. 또한 baseline 선형 회귀 모델을 생성하여 향후 게시물에 대한 모델링 노력을 비교
time_cycles를 점검할 때 가장 먼저 고장난 엔진은 128사이클 후에 고장난 반면, 가장 오래 작동한 엔진은 362사이클 후에 고장난 것을 볼 수 있다. 또한 데이터 세트 설명은 터보팬이 단일 작동 조건에서 실행된다는 것을 나타낸다.
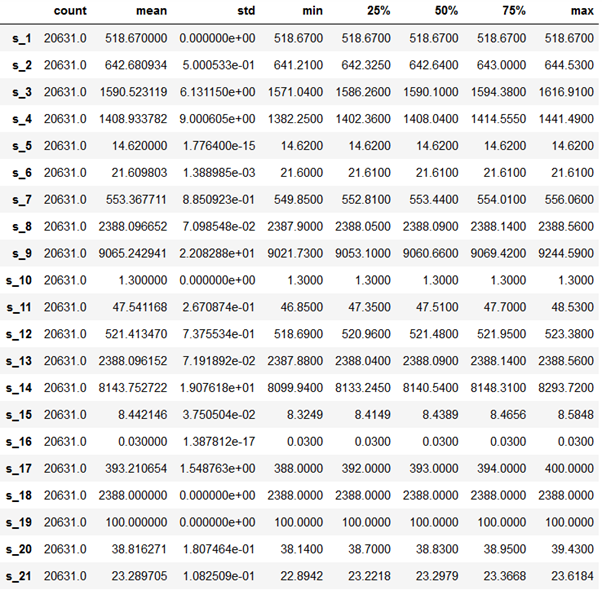
표준 편차(std)를 살펴보면 명확한 센서 1, 10, 18 및 19는 전혀 변동하지 않으며, 유용한 정보가 없으므로 안전하게 폐기할 수 있다. 분위수(Quantile)를 검사하는 것은 센서 5, 6, 16의 변동이 거의 없으며 추가 검사가 필요하다는 것을 나타낸다. 센서 9와 14의 변동률이 가장 높지만, 이것이 다른 센서가 중요한 정보를 보유하지 못한다는 것을 의미하지는 않는다.
Computing RUL
먼저 RUL에 대한 target값을 계산한다. target variable은 두 가지 용도로 사용된다
- 센서 신호를 플로팅하는 동안 우리의 X축 역할을 할 것이며, 우리가 센서 신호의 변화를 엔진이 거의 고장날 때 쉽게 해석할 수 있게 해 준다.
- 우리의 supervised(지도)된 기계 학습 모델의 대상 변수로 작용할 것이다.
RUL은 시간이 지남에 따라 선형적으로 감소하고 엔진의 마지막 시간 사이클에서 값이 0이라고 가정한다(UL이 고장 전 10 사이클에서 10, 고장 전 50 사이클에서 50이 된다)
RUL target variable 계산 : unit_nr별로 그룹화하여 max_time_cycle 계산, max_time_cycle에서 time_cycle을 빼서 RUL을 구함. max_time_cycle은 필요 없으므로 삭제
Plotting(시각화)
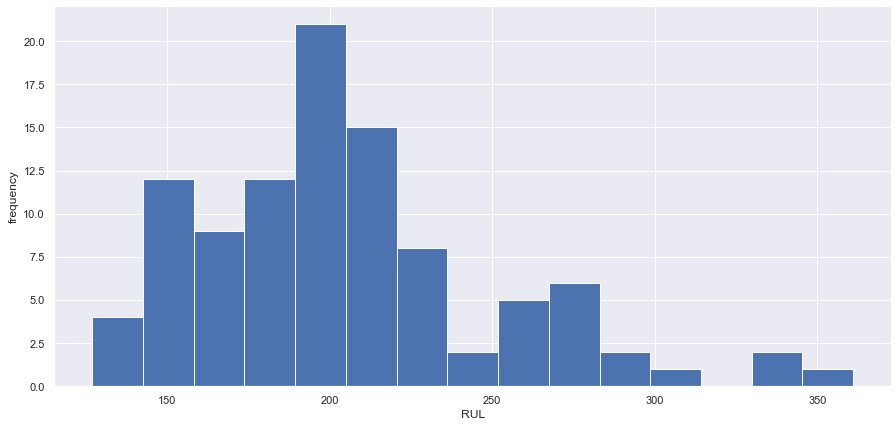
최대 RUL의 히스토그램을 표시. 대부분의 엔진이 약 200사이클 동안 고장나는 것을 재확인. 또한 분포가 오른쪽으로 치우쳐 있으며, 300회 이상 지속되는 엔진은 거의 없다.
이후 그래프는, 10으로 나뉘는 unit들의 센서 값들을(한 그래프당 한 센서의 10으로 나뉘는 unit 당 값) 그린 그래프이다. X축을 되돌려서 RUL이 축을 따라 감소하며, RUL이 0이면 엔진 고장을 나타낸다. 센서 5, 6, 16의 그래프를 확실히 검사해야 한다는 것을 기억하라.
- 센서 1, 10, 18, 19의 그래프는 유사함. flat line. 센서가 유용한 정보를 보유하지 않음. 센서 5,16도 마찬가지. 제외해야할 센서임. 모든 시간 동안 일정하게 유지되기 때문에 RUL과 관련된 정보를 보유하지 않는다.
- 센서 2와 센서 3, 4, 8, 11, 13, 15 및 17은 상승 추세를 나타냄
- 센서 6의 센서 수치는 때때로 하향 피크를 이루지만 감소되는 RUL과 명확한 관계가 없는 것으로 보임.
- 센서 7은 센서 12, 20 및 21에서도 볼 수 있는 감소 추세
- 센서 9는 센서 14와 유사한 패턴
--> 1,5,6,10,16,18,19를 제외한 나머지 센서를 예측 변수로 사용
Baseline Linear Regression
모델을 평가하기 위해 RMSE를 선택. 예측이 평균적으로 얼마나 많은 시간 사이클이 꺼지는지를 나타내며, 우리가 사용하는 독립 변수에 의해 설명될 수 있는 종속 변수의 비율을 나타내는 설명 분산(또는 R² 점수)을 제공하기 때문
train 데이터를 X_train(target 값 없음), y_train(target 값만 포함)으로 나누고, X_test는 target 값이 없는 상태임. 주어진 true RUL 값이 존재하니까.
LinearRegression() 부르고 fit, predict, evaluate 진행. 독특하게 여기선 X_train, X_test 둘 다 predict evaluate함. 모델이 제시된 데이터로 어떻게 행동하는지 전체 그림을 얻기 위해라고 함...
returns
train set RMSE:44.66819159545453, R2:0.5794486527796716
test set RMSE:31.952633027741815, R2:0.40877368076574083
test에서 RMSE이가 더 낮음. 보통 train에서 좋은 결과가 나와야 하기 때문에 직관적이지 않음. 왜그럴까?
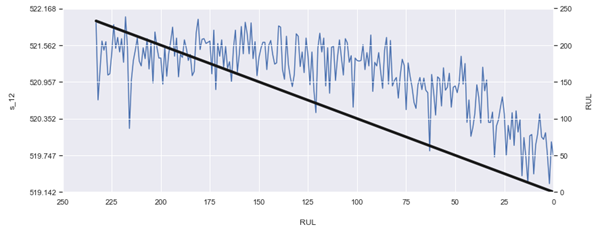
300s까지 ranging well된 계산된 RUL 때문일 수도 있음. 아래 그래프의 추세를 보면, 선형적으로 계산된 RUL의 higer value 부분은 센서 신호와 잘 상관되지 않는 것으로 보인다. test set의 RUL 예측 값이 failure와 가깝고, lower target RUL과 센서 시그널의 상관관계가 명확했기에 test set를 정확하게 예측하는게 더 쉬웠을 수도 있다. train과 test set 사이의 RMSE 차이는, 우리의 RUL 가정(예측)의 결점이며 우리가 개선해야할 점이다.
