1편에서는 RMSE 31.95의 기준 선형 회귀 모델을 적용했다. 결과를 더욱 개선하기 위해 정확성을 높이고 Support Vector Regression(SVR)을 사용하기 위해 RUL에 대한 가정을 다시 검토한다.
Loading data
여기 과정은 1편과 동일. 단 모델 성능을 evaluate 함수를 새로 정의한다. mse, rmse 사용.
Re-examining RUL
1편에서는 RUL이 선형적으로 감소한다고 가정했으나, 끝부분에서 이것이 전체 모델 성능에 영향을 미칠 수 있음을 확인함(RUL이 큰 부분에서 오차가 크게 발생 -> test train set간의 성능 차이)
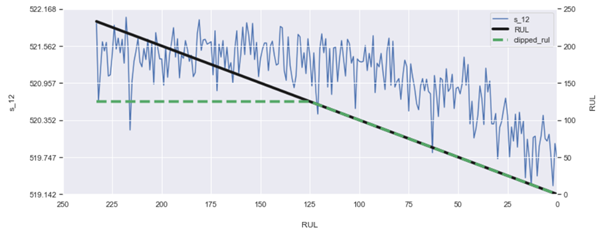
센서 신호들을 보면 많은 센서가 처음 부분에서는 다소 일정해 보인다. 엔진이 시간이 지남에 따라 고장을 일으키기 때문이다. 선의 굴곡이 생기는 부분(뭐라고 표현하더라 팔꿈치? 아무튼 꺾이는 부분)은 엔진이 저하되고 있다는 것을 나타내는 첫 정보 비트이며 처음으로 RUL이 선형적으로 감소하는 부분이라고 가정하는 것이 타당함. 우리는 초기의 마모(initial wear)에 대한 정보가 없기에 그 시점 이전의 RUL에 대해 아무 것도 말할 수 없다(판단할 수 없다)
RUL이 선형적으로 감소하는 대신, 우리는 우리의 RUL을 상수로 시작하여 일정 시간 후에 선형적으로만 감소하도록 정의.
- 초기 상수 RUL은 초기 상수 평균 센서 신호와 더 잘 상관(correlate)된다.
- RUL에 대한 피크 값이 낮을수록 대상 변수의 확산이 감소하므로 선 적합이 용이함.
결과적으로, 이러한 변화를 통해 회귀 모델은 낮은 RUL 값을 더 정확하게 예측할 수 있다. 낮은 RUL 값을 정확하게 예측하는 것이 사실 제일 흥미롭고 중요한 부분임.
이전의 선형 감소 RUL을 원하는 상한 값(desired upper bound value)으로 클리핑하자. 125에서 clipping한 값이 여러 상한 값을 테스트한 결과 모형이 가장 크게 개선되었다. train set에 대한 가정을 updating하는 과정이므로 evaluation에 이 변경을 포함하자. 단 test set의 true RUL 값은 유지하라.
returns
train set RMSE:21.491018701515415, R2:0.7340432868050447
test set RMSE:21.900213406890515, R2:0.7222608196546241
train RMSE가 절반 이상 줄어들었다. 더 중요한 것은 test set의 개선이다. 31.95에서 21.90으로 31% 향상.
Support Vector Regression
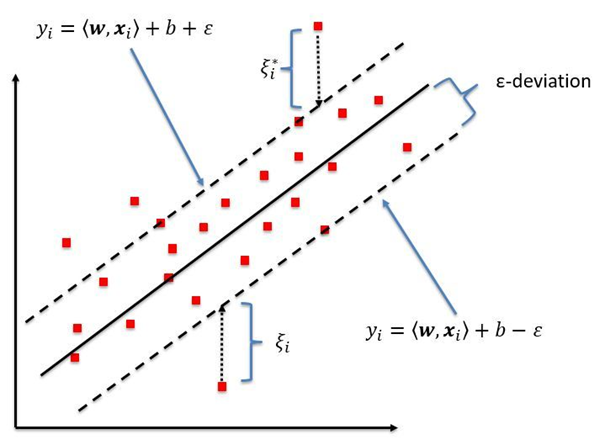
검은 실선은 target 값을 표현, 검은 점선은 distance epsilon의 범위를 나타냄. 바운더리 밖의 값들만이 model fitting과 loss function을 감소시키는데 기여함. loss functiondms Ridge와 Lasso 회귀와 유사함
선형 SVR은 주로 기준 데이터에서 엡실론(θ) 거리에 경계를 설정. model fitting에서 loss function을 최소화 할 때 경계 내의 점들은 무시된다. 즉 경계 밖의 점에 모델을 fitting하여 computational load(계산 부하)를 줄이고 복잡한 동작을 캡처하지만, outlier에 예민함
SVR 함수를 부르고 fit, predict, evaluate 진행
returns
train set RMSE:29.57783070266026, R2:0.49623314435506494
test set RMSE:29.675150117440094, R2:0.49005151605390174
선형 회귀 분석보다 결과가 안좋음
Scaling
SVR은 feature vector 사이의 거리를 비교해서 작동한다. 그러나 feature들이 범위에 따라 다르다면, 계산된 거리는 큰 범위에 의해 지배된다.
따라서 feature들을 동일한 범위 내로 scale하자. 이를 통해 SVR은 상대 거리를 비교하고 대략적으로 동일한 가중치의 변동을 가질 수 있다.
train data에 MinMaxScaler를 사용하여 범위를 0~1로 맞춘다. X_train 및 X_test set 모두에 적용.
returns
train set RMSE:21.578263975067888, R2:0.7318795396979632
test set RMSE:21.580480163289597, R2:0.730311354095216
개선됌
Feature engineering
매우 유용한 feature 엔지니어링 기법은 feature의 다항식 조합을 만드는 것인데, 이러한 조합은 원래 feature에서 명확하지 않은 데이터 패턴을 나타낼 수 있다. (s_2와 s_3의 2차원으로 다항식 특징을 만들고자 한다면, 결과는 [1, s_2, s_3, s_2θ, s_3θ, s_2*s_3] ) 현재 데이터 세트의 모든 센서에 적용하면 feature 공간이 14개에서 120개로 늘어난다.
PolynomialFeatures() 함수를 부르고 fit, transform 진행. 그 후 SVR fit, predict, evaluate
returns
train set RMSE:19.716789731130874, R2:0.7761436785704136
test set RMSE:20.585402508370592, R2:0.75460868821153
개선된 결과를 통해, 이러한 다항식 feature 조합을 통해 추가적인 정보를 얻었음을 확인. 로그 변환도 고려했지만 센서 value가 이러한 transform을 적용하기에 충분히 크지 않았음.
다항식 feature은 feature space를 증폭시키고 모델을 팽창하게 만들어 train 시간을 증가시켰다. 이를 완화시킬 수 있는 방법이 있을까?
Feature selection
engineered feature들을 통해 어떤 feature가 모델 성능에 큰 기여를 하는지 계산할 수 있다. 이를 위해 SelectFromModel을 사용, 훈련된 모델을 전달하고 prefit을 True로 설정하자. 중요한 feature를 선택하는 threshold를 'mean'값으로 설정하여 선택한 피쳐가 전체 세트의 평균 피쳐 중요도보다 더 큰 피쳐 중요도를 가질 것임을 나타낸다 평균보다 더 높은 피쳐의 중요도를 나타내는 Boolean array를 return받는다. 이를 통해 'feature importance > mean feature importance'인 feature들만 유지한다.
SelectFromModel(svr_f, threshold='mean', prefit=True) 함수 부르고 get_support를 통해 중요한 feature를 받는다. 여기서 svr_f는 아까 증폭시킨 다항식 feature들. SVR fit predict evaluate
returns
train set RMSE:19.746789101481127, R2:0.775461959316527
test set RMSE:20.55613819605483, R2:0.7553058913450649
RMSE가 조금 개선됨과 동시에 120개에서 37개의 feature 개수로 줄어듬! 이러한 개선은 아마도 train set에서의 model overfitting이 조금 줄어들었기 때문일 것.
Selecting our final model
최종 모델의 경우 train set에 대한 간단한 하이퍼 파라미터 튜닝을 사용하여 엡실론의 값을 튜닝한다. 엡실론은 손실 함수를 최소화하면서 고려해야 할 데이터 포인트의 경계를 나타낸다. 0.2의 엡실론이 훈련 세트에서 가장 좋은 성능을 내는 것으로 보인다.
우리의 최종 모델은 경계 조정 SVR, train에 클리핑된 RUL, feature 스케일링 및 가장 기여도가 높은 2차 다항식 특징을 활용하여 테스트 RMSE 20.54에 도달한다. SVR은 선형 회귀에 비해 확실히 개선된 것이지만, 업데이트된 RUL 가정과 비교하면 개선 효과가 미미하다.
