CMAPSS EDA #5 (RandomForest, Hyperparameter tuning, Randomsearch, GroupKFold)

먕먕·2022년 6월 12일

이전 편에서 생존 분석을 살펴보고 FD001에 대한 분석을 했다. 최종 RMSE는 초기 모델에 비해 좋지 않았지만 검열된 데이터를 다룰 수 있기에 흥미로운 기술이었다. 이번 편에서는 FD003에 대해 분석을 해보겠다. 이 데이터 세트는 두 가지 가능한 고장 모드를 가진 엔진이다. (FD002는 더 복잡하여 다양한 작동 조건을 처리하기 위한 전처리/모델링이 필요해보인다)

Exploratory Data Analysis(EDA)

데이터를 불러온다. 엔진의 최초 고장 시점은 145 cycle이며 가장 마지막 고정 시점은 525 cycle이다. std를 고려하여 센서 1,5,16,18,19는 정보를 갖고 있지 않다고 판단, 삭제한다. RUL(max cycle - time cycle)을 계산하여 train set에 추가한다.

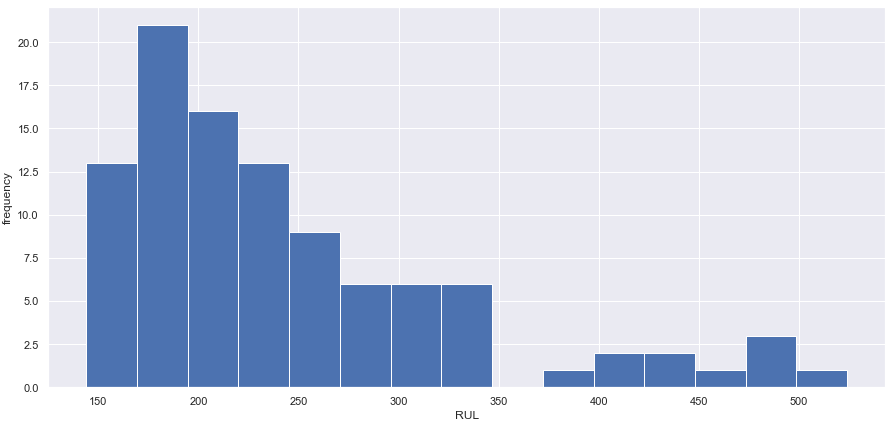
RUL 분명히 오른쪽으로 치우쳐 있고 왼쪽 꼬리 부분에 별로 없다. 치우친 분포는 모형 성능에 큰 영향을 미칠 수 있다. EDA가 완료된 후, train set의 RUL을 125로 clipping 할 것이다.

Plotting signals

센서 1,5,16,18,19는 아무 정보도 갖고있지 않음을 확인할 수 있다

센서 2,3,4,8,11,13,17은 유사하게 증가하는 트렌드를 볼 수 있다.

센서 6은 약간 독특하다.

센서 7,12,15,20,21은 명확하게 두 가지의 고장 모드를 보여준다.

센서 9,14는 비슷한 추세를 보이지만 고장 모드를 잘 구분하지 못한다. 모델 성능에 미치는 그들의 영향을 테스트하는 것은, 그들이 모델에 포함될지 말지를 point out 해내야한다

센서 10 또한 독특한 추세를 보이지만 어쨌든 증가하는 모양을 띈다.

Baseline model

가장 간단한 모델로 시작한다. 추가적인 전처리 없는 회귀 모델로 시작하자. 필요 없는 센서들을 제거하고 RUL clipping만 진행한다.

returns

train set RMSE:19.33013490506061, R2:0.7736110804777467
test set RMSE:22.31934448440365, R2:0.7092939799790338

Random Forest

single decision tree에 비해 Random Forest(RF)가 갖는 강점 중 하나는 다양한 트리를 생성할 수 있는 능력이다.
single decision tree를 생성할 때 알고리즘은 데이터 집합을 가장 잘 분할하는 하나의 feature에 기반을 둔다. 다음 노드에서는 또 다시 모든 feature 중 가장 잘 분할하는 하나를 재검사 할 것이다. 이러한 조건에서 decision tree를 두 번째로 fit하면 트리가 정확하게 동일하다.
RF는 분할 할 때 모든 feature의 부분 집합을 고려한다. 이것은 알고리즘이 다른 트리를 만들도록 강요하는데, 최상의 분할을 만드는 feature를 사용할 수 없을 수 있기 때문이다. 잠재적으로 regular decision tree의 단일 최상의 분할보다 더 나은 분할의 조합을 생각해낸다.

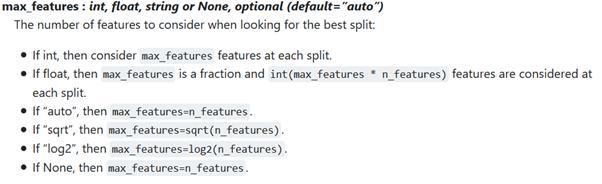
sklearn 문서를 참고하면 (max_feature = 'auto' then max_features = n_features) RF regressor는 기본적으로 모든 feature들을 고려하며, 동일한 트리를 반복적으로 생성한다. 따라서 max_features를 사용 가능한 feature의 제곱근으로 지정한다. 또한 random_state를 설정하여 트리가 항상 동일한 방식으로 생성되도록한다. 그렇지 않으면 랜덤 트리 생성은 모델 결과에 영향을 미치므로 일부 feature를 변경했거나 랜덤성으로 인해 모델이 더 나은 성능을 발휘하는지 판단하기가 어렵다.
RandomForestRegressor(n_estimatores=100, max_features="sqrt", random_state=42)

returns

train set RMSE:5.9199939580022525, R2:0.9787661901585051
test set RMSE:21.05308450085165, R2:0.7413439613827657

RF가 성능을 조금 높였지만 train과 test set사이의 차이는 아마 overfit이 발생했기 때문일 것이다.
tree_.max_depth와 tree_.n_node_samples를 통해 가장 긴 경로의 노드 개수와 마지막 노드의 샘플 개수를 알아보자. 가장 긴 경로는 33개의 노드로 구성되며 이는 우리가 넣은 feature의 2배가 넘는다. 마지막 노드에는 sample들이 거의 포함되지 않음을 볼 수 있다. 즉 트리가 너무 구체적이어서 대부분의 샘플이 구별될 수 있을 때까지 분할 기준을 생성했는데, 이는 일반화에 정말 좋지 않다(따라서 train set에 overfitting). RF의 max_depth와 min_samples_leaf를 설정하여 이 문제를 해결하자.
RnadomForestRegressor(n_estimatores=100, max_features="sqrt", random_state=42, max_depth = 8, min_samples_leaf=50)

returns

train set RMSE:15.706704198492831, R2:0.8505294865338602
test set RMSE:20.994958823842456, R2:0.7427702419664686

overfitting이 약간 줄고 성능이 향상되었다. 센서 6과 10은 포함된 결과이다(포함된 결과가 더 좋다)

Visualize RF

트리 중 하나를 시각화해서 개선 시점을 잡아보자

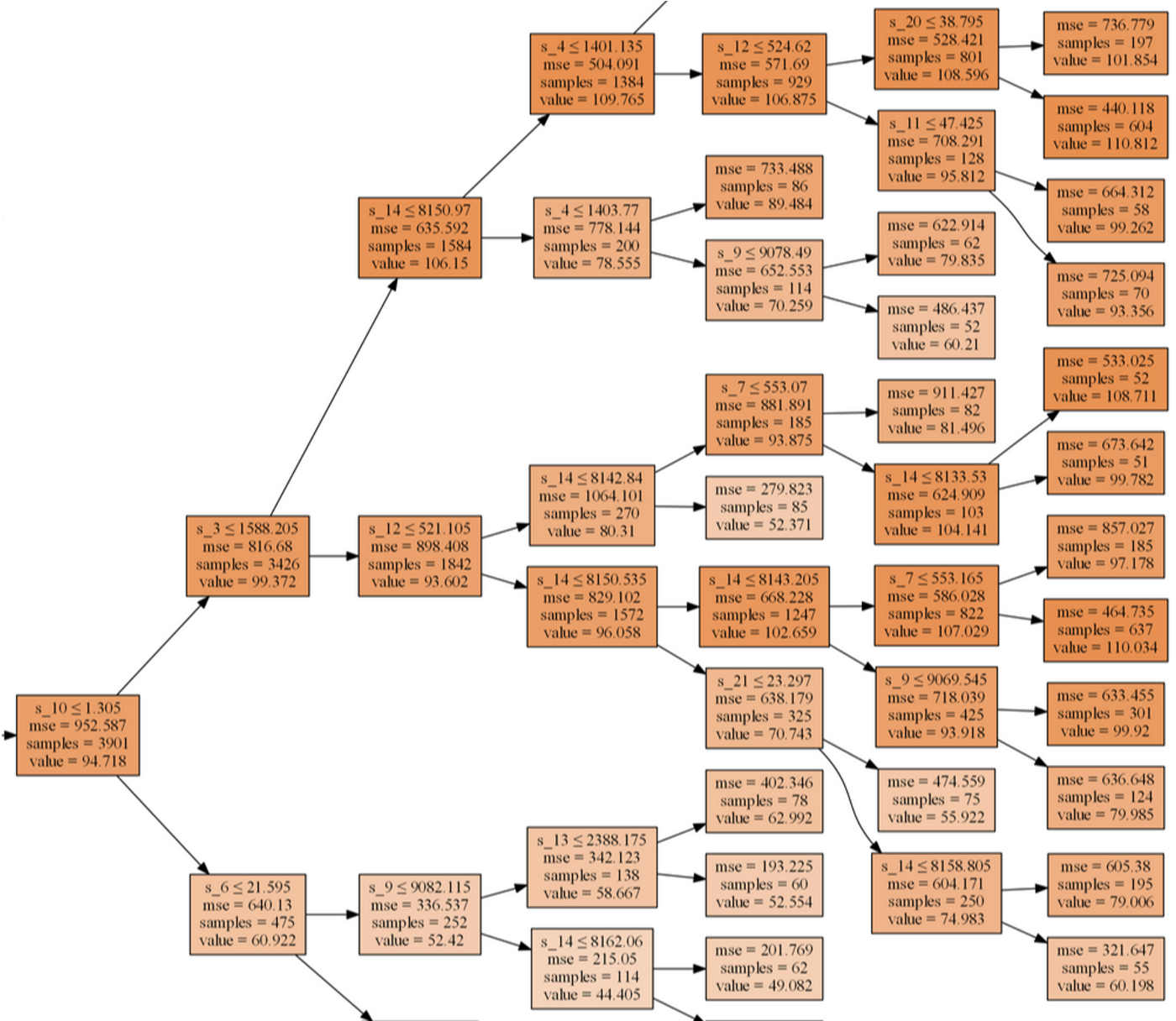
mse>500인, 부정확한 예측을 이끌어내는 일부 노드가 존재하는 것 같다. 센서 9와 14가 그랬던 것을 기억해보자. 이 두 센서는 분할 기준으로 꽤 많이 사용되었으나 결과가 좋지 않다. 이 둘을 제외해보자.

train set RMSE:17.598192835079978, R2:0.8123616776758054
test set RMSE:22.186214762363356, R2:0.7127516253047333

성능이 더 좋지 않다. 다시 포함하자.

A word on feature engineering

feature enginerring에 대한 가능성이 적다. RF는 이미 복잡한 데이터 패턴을 학습하는데 탁월하다. 우리가 할 수 있는 것이 많지 않다.
moving average를 사용해 보았다. 이 이론은 분할을 정확하게 적용하는 것에 도움을 주고 signal에서 noise를 제거할 때 결점들을 구분하기 쉽게 한다. 그러나 성능은 증가하지 않았다.
hyperparameter tuning을 해보자.

Hyperparameters

어떤 매개변수를 조정할 수 있을까
rf.get_params()

RF의 가장 큰 도전점은 overfitting이다. 매개 변수 max_depth, min_samples_leaf, ccp_alpha 및 min_inpurity_decrease는 overfitting을 줄이고 전반적으로 더 나은 성능 모델을 생성하는 데 도움이 된다.

ccp_alpha
Cost complexity pruning alpha. pruning(가지치기)에 사용되는 매개변수이다. 가지치기는 fitting 이후 노드를 제거하는 것으로 보통 overfitting을 방지하기 위해 min_sampels_leaf와 max_depth를 사용하는 것의 대안책이다. 노드의 cost complexity는 fitted tree에서 찾을 수 있다.
ccp_alpha가 낮을수록 cost complexity는 높다. 즉 ccp_alpha가 작은 노드를 제거하여 tree를 가지치고 전체적 복잡성이 감소한다.
ccp_alpha의 범위를 확인하기 위해 effective alpha 대 impurity를 시각화해보자.

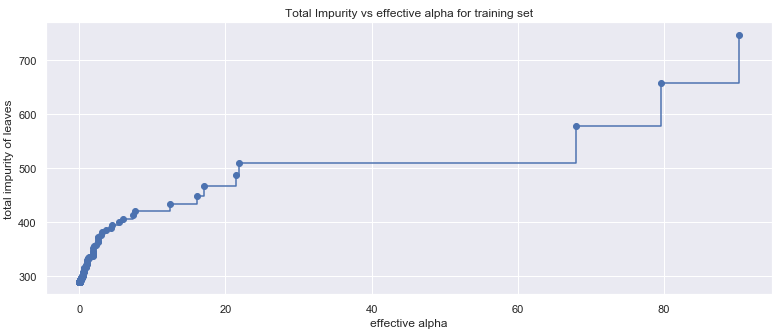
effective alpha가 70에서 20 이상으로 떨어지면 트리의 cost complexity는 실제로 증가하지만 alpha가 낮을 경우 leaf impurity에 미치는 cost complexity의 영향을 파악하기 어렵다

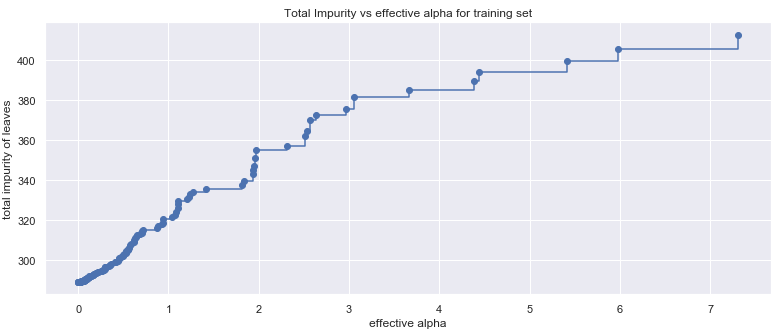
effective alpha가 2에서 0으로 떨어지면(cost complexity가 최대에 도달하면) leaf impurity는 50 이상 감소하며 which amounts to ~7 training RMSE(?).

min_impuritydecrease
분할 후 오차의 감소를 나타내는 척도이다. 일반적으로 single decision tree에 대해 계산된다. 따라서 단일 트리에서 필요한 정보를 추출하고 계산해보자.

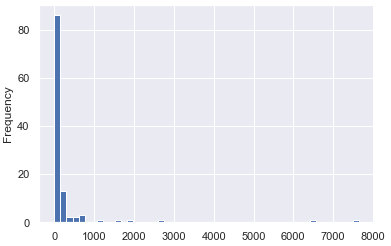
매우 오른쪽으로 치우쳤다. 즉 트리의 처음 몇 개의 노드가 오류 감소에 많은 기여를 했다는 것이다. impurity decreasedml 25%가 14.59보다 작음을 알 수 있다. 따라서 이 값을 매개변수로 쓰자.

Randomsearch

매개변수의 범위를 지정해보자

max_depth = [None] + list(range(3, 34, 3))
min_samples_leaf = list(range(1, 102, 10))
min_impurity_decrease = list(np.arange(0,147)/10)
ccp_alpha = list(np.round(np.linspace(0, 2, 81), decimals=3))

조합해보면 150만개 이상의 조합이 나온다. 따라서 60개의 고유 조합을 랜덤하게 선택해 Randomsearch를 적용하자. 반복 횟수가 늘어나면 좋은 해결책을 찾을 가능성이 올라간다. Randomsearch 대신 tree 수를 적게해 훈련 시간을 빠르게 하는 것도 좋다.

그 전에 선택한 매개변수의 유효성을 검사하기 위한 검증 세트를 만들자.

Validation

train 세트에 포함된 엔진은 validation test 세트에 포함될 수 없으며, 그 반대의 경우도 마찬가지이다.
일반적으로 데이터의 80%가 교육 세트에 속하고 20%가 검증 세트에 속하는 랜덤 분할을 생성한다. 그러나 단위 번호를 고려하지 않고 무작위로 분할하면 열차와 검증 세트에서 단일 엔진의 데이터 일부가 될 수 있다. 이러한 'data leakage'를 방지하기 위해 단일 엔진의 모든 기록이 training과 validation set 중 하나에 기록되는 GroupKFold를 사용하자. 여기서 GroupKFold는 RandomizedSearchCV의 인스턴스로 활용되는데, 'unit_nr'에 따라 분할된다.
RandomForestRegressor() GroupKFold() RandomizedSearchCV()
gkf = GroupKFold(n_splits=3)
cv=gkf.split(train, groups=train['unit_nr']

'min_samples_leaf': 11, 'min_impurity_decrease': 0.0, 'max_depth': 15, 'ccp_alpha': 0.125

가장 좋은 파라미터 조합

Final model

RandomForestRegressor(n_estimators=100, max_features="sqrt", random_state=42, min_samples_leaf=11, min_impurity_decrease=0.0, max_depth=15, ccp_alpha=0.125)