CMAPSS EDA #6 (NN, GroupShuffleSplit, MLP, Condition-based standardization, lag, smoothing, Exponential weighted moving average, Hyperparameter tuning)
이전 편에서는 FD003에 대해서 RF와 hyperparameter tuning을 진행했다. 이번 편에서는 FD002에 대한 모델을 개발하겠다. 엔진이 6가지 고유한 작동 조건에서 작동할 수 있는 데이터 세트이다. 복잡한 데이터 세트인만큼 NN(신경망)을 훈련하는 방법으로 진행하려 한다.
Loading data
데이터를 load하고 RUL 계산을 진행.
EDA
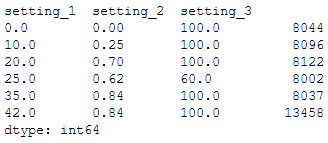
각 setting별로 round()해서 조합을 보면 6가지의 조합이 존재함을 알 수 있다.
Plotting
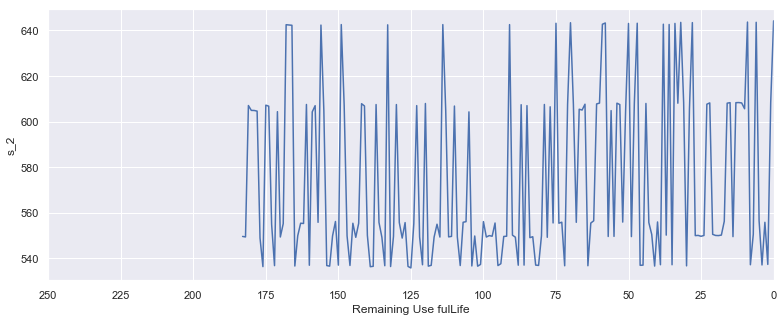
한 센서의 시그널을 plotting 했다. 이전과 다르게 어떠한 경향도 보이지 않는다. FD002는 엔진에 대한 다양한 작동 조건을 포함한다. setting별로 보자.
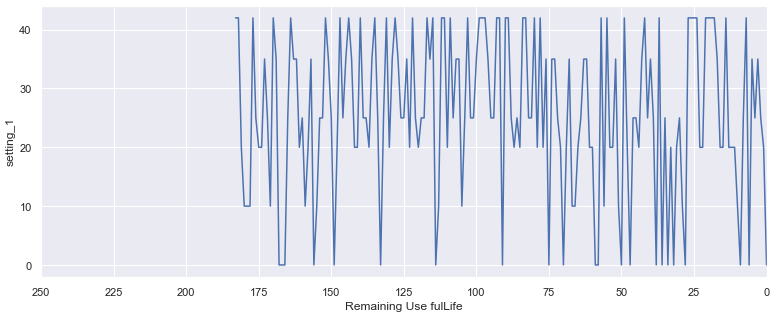
setting 1과 2는 비슷한 추이를 보이며
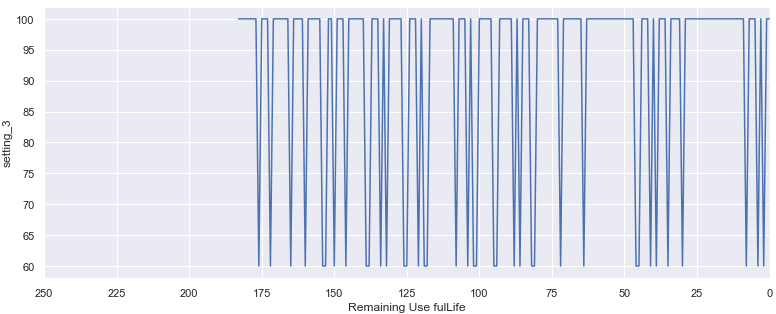
setting 3은 조금 다르다.
무엇을 알 수 있을까. 다른 조건에서 다른 엔진들이 작동할 것이라 예상했지만, 작동 조건이 cycle마다 바뀌는 것이다. 복잡하다.
Baseline model
baseline model은 단순한 선형회귀이다. RUL를 125로 clipping하기만 하자.
returns:
train set RMSE:21.94192340996904, R2:0.7226666213449306
test set RMSE:32.64244063056574, R2:0.6315800619887212
Validation set
신경망(Neural Network, NN)은 overfitting 하기 쉽다. 따라서 validation set을 사용하는 것이 필요하다. 'data leakage'를 방지하기 위해 sklearn의 GroupShuffleSplit을 사용해 unit number으로 구성된 그룹으로 분할하자.
gss = GroupShuffleSplit, gss.split(groups = train['unit_nr']
validation 집합은 train과 validation 집합 간의 모델 성능을 비교하기 위해 유사한 분포를 가져야 한다. 데이터 세트의 유사성을 파악하기 위해 target 변수 분포를 확인하자.
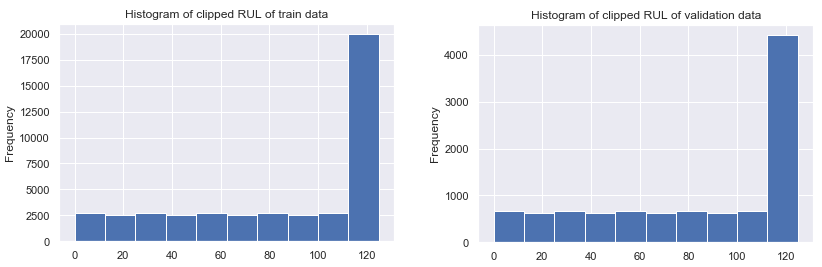
frequency는 낮지만 validation RUL의 분포는 train RUL과 유사하다.
Scaling
Support Vecotr Regression(SVR)과 마찬가지로 NN은 상대 거리를 사용하는 경향이 있으나 절대 차이를 이해하는데 좋지 않다. 따라서 스케일링이 필요. SVR 때와 마찬가지로 MinMax 사용.
Multilayer Perceptron (MLP)
MLP는 NN의 vanilla로 비선형 패턴을 학습하는 데 적합하고 적어도 입력, 숨김 및 출력 계층으로 구성된다. 몇개의 Dense 층으로 구성된 model을 만들고 compille한다. 단 마지막 층은 단일 노드를 출력해야하는데, RUL 값 하나를 출력해야하기 때문. compile 단계에서 랜덤 가중치가 초기화되며, 가중치를 업데이트하는 optimizer와 loss 함수를 정의한다. 그 다음 fit으로 train을 시작, 이때 loss의 감소에 주의하자. 두 손실이 모두 감소했을 때가 잘 진행되고 있는 과정이며 train은 감소하나 test는 증가할 시 overfitting이다. plotting으로 loss를 쉽게 해석할 수 있다.
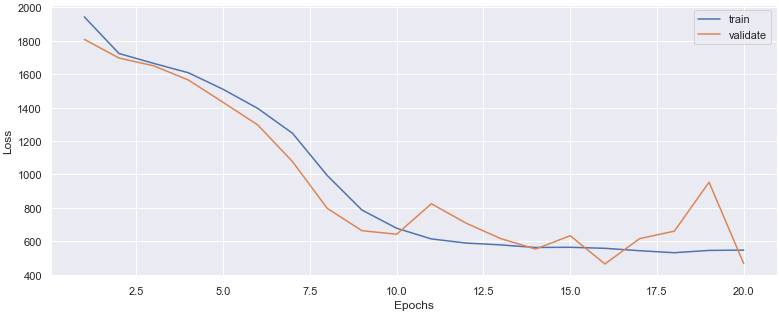
returns:
train set RMSE:22.393854937161706, R2:0.7111246569724521
test set RMSE:34.00842713320483, R2:0.600100397460153
baseline model과 비슷한 성능을 내는 NN을 만들었다. 이제 feature engineering을 진행해보자.
One hot encoding
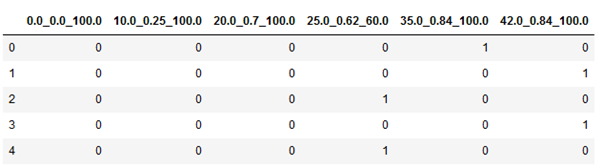
각 작동 조건을 카테고리로 만들자. 이렇게 했을 때 개선(train RMSE = 20.80, test RMSE = 32.01)이 이루어졌지만, 이 구현에는 두 가지 문제가 있다.
- 개선폭이 기대한 것 만큼 크지 않았다.
- 이 개선은 추가적 feature engineering을 거의 하지 못하게 한다. 예를 들어, 센서 신호가 작동 조건들 사이에서 벗어날 경우 사용할 수 없다. 또한 lagged variable을 추가하는 것은 작동 조건의 변화를 고려해야하기에 비실용적이다.
다른 방법을 찾자
Condition-based standardization
이전에 우리는 minmax scaler를 사용해 scaling 했다. condition-based standardization에서는 모든 기록을 한 작동 조건으로 그룹화해서 standard scaler를 적용한다. 이러한 스케일링은 그룹화된 작동 조건의 평균을 0으로 만든다. 각 작동조건에 대해 별도로 적용하기 때문에 모든 신호는 평균 0 값을 받게 되며, 비교하기 쉽게 한다.
이러한 유형의 standardization은 신호가 비슷한 동작을 하지만 다른 평균을 중심으로 하는 경우 매우 잘 작동한다. 이 기술은 작동 조건 자체가 고장 임박에 영향을 미치지 않는 경우에만 사용할 수 있다!
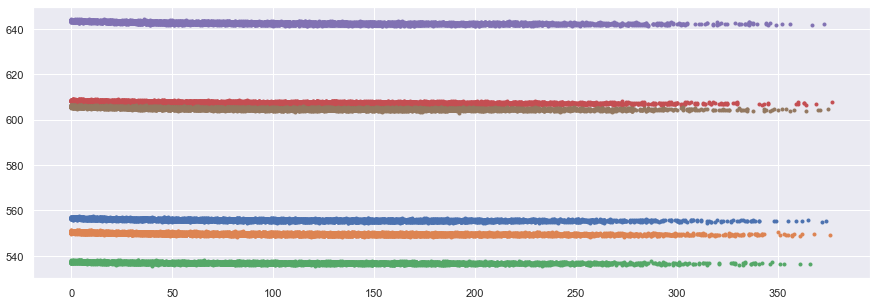
먼저 작동 조건을 df에 추가한다. 각 신호들이 다른 평균을 갖지만 비슷한 동작을 한다는 것을 증명하기 위해 모든 엔진의 각 센서들의 작동 조건을 표시한다.
condition-based standardization을 추가하고 시그널들을 plot해서 확인해보자
센서 1,5,16,19는 비슷해보이지만 이 시점에서 딱히 유용해보이진 않는다.
센서 2,3,4,11,15,17은 비슷한 상향 트렌드를 보인다.
센서 6,10,16는 비슷해보이나 유용한 정보를 갖고있어보이진 않는다.
센서 7,12,20,21은 유사한 하향 트렌드를 보인다.
센서 8,13은 닮아보이지만, standardization이 끝 부분에서는 잘 작동하지 않은 것 같다. 신호가 계속 up down 점프하고 있기 때문이다. 좀 더 노이즈가 섞여있긴 하지만 센서 9와 14와 유사해 보이지 않나 예상한다. 일단은 유지하자.
센서 9,14는 노이즈가 덜 섞인 8,13과 유사해보인다.
센서 18은 아무런 정보도 갖고 있지 않다.
센서 2,3,4,7,8,9,11,12,14,15,17,20,21을 갖고 계속 진행해보자. 이 센서들만 model에 넣어서 compile, fit, predict, evaluate하자.
returns:
train set RMSE:19.35447487320054, R2:0.7842178390649497
test set RMSE:29.36496528407863, R2:0.7018485932169383
Lagged variables
시계열 관련 이전 포스팅 참고. lagged 변수를 추가하여 모델에 이전 시간 주기의 정보를 제공할 수 있다. 여러 주기의 정보를 결합하면 모델이 추세를 탐지하고 데이터를 보다 완벽하게 볼 수 있다.
이전 포스팅에서 잘 작동했던 lag들의 집합 [1,2,3,4,5,10,20]으로 훈련.
drop sensor, condition_scaler(), add_lags, compile, fit, predict, evaluate
returns:
train set RMSE:17.572959256116462, R2:0.8236048587786006
test set RMSE:29.075227321534157, R2:0.7077031620947969
A word on stationarity and smoothing
정지 데이터는 신호의 통계적 특성이 시간이 지남에 따라 변하지 않는다는 것을 의미한다. condition-based standardization이후, adfuller test를 통해 data가 stationary한지 확인하라. 약간의 trend가 보이지만 대부분(전부는 아님)에 참인 정지로 간주할 수 있다.
introducing smoothing
exponential weighted moving average를 사용하자. 간단하지만 매우 강력하다. 필터링 된 값을 계산할 때, 현재 값과 이전 필터링 된 값을 함께 고려한다.
~Xt = aXt + (1 - a)~Xt-1
알파는 필터의 강도로, 0~1 사이의 값을 갖고 예를 들어 0.8인 경우 Xt(현재 값)에서 80, ~Xt-1(필터링된 이전 값)에서 20의 필터링이 된다. 즉 알파 값이 작을 수록 smoothing이 강해진다(이전 값의 영향을 크게 받음)
pandas에서는 exponential weighted function에 해당 필터가 들어있다.
apply(lambda x: x.ewm(alpha=0.4).mean()
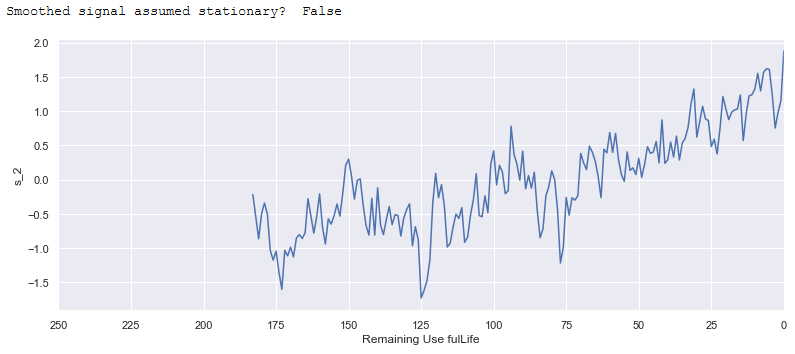
smoothing 이후에는 더이상 stationary하지 않다. alpha값에 따라(작을 수록 강한 smoothing) 신호의 노이즈가 smoothing 될 수록 일반적인 추세가 더 뚜렷해지므로 점점 덜 정지되어 보인다. 따라서 정지 상태가 되려면 데이터 세트의 row에서 더 많은 감소가 필요하다. alpha가 0.69 미만일때 일부 엔진의 모든 행이 삭제되므로 알파가 0.69보단 커야하지만, 효과가 그리 크지 않았다. 강한 smoothing이 더 나은 모델 성능을 제공하므로 정지 상태는 포기하자.
returns:
train set RMSE:15.916032412669667, R2:0.85530069539296
test set RMSE:27.852681524828476, R2:0.731767185824673
test RMSE가 많이 줄었다.
동일 모델을 사용해 validation loss가 어떻게 행동하는지 epochs를 당겨보자. 더 많은 epoch에도 상대적으로 일정하게 유지한다면 파라미터 튜닝에서 더 많은 epoch을 사용해도 된다는 뜻이다.
returns:
train set RMSE:19.784558538181454, R2:0.7764114588121707
test set RMSE:32.17059484378398, R2:0.6421540867400053
50 epochs를 사용한 결과, test rmse가 증가했다. 10~30 사이의 epochs를 사용하자. drop out으로 overfitting 방지를 할 것이다.
Hyperparameter tuning
alpha, lags, epochs, number of NN, nodes per layer, dropout, optimizer&learning rate, activation function, batch size 등의 고려해야할 매개변수가 존재한다.
RF처럼 할 수는 없다. 각각의 매개변수는 다 다른 위치에서 조정되어야하기 때문이다.
해당 튜닝은 random search로 간주될 수 있다. 60회 반복하면 최상의 솔루션의 95% 이내에 도달할 수 있다. 더 많은 반복을 통해 최상의 솔루션에 가까워질 수 있다. 반복 횟수를 100회로 설정했다. 각 반복에 대해 정의된 매개 변수 목록에서 하이퍼 매개 변수 값을 랜덤하게 샘플링한다. 이러한 매개 변수를 기반으로 데이터 세트가 전처리되고 모델이 생성된다. cross-validation을 위해선 소개한 그룹 셔플 분할을, 하이퍼 파라미터 튜닝의 경우는 3 splits을 사용한다.
훈련 후 사용된 매개 변수, 유효성 검사 손실의 평균 및 표준 편차를 저장한다. 유효성 검사 손실의 표준 편차는 데이터 세트의 유효성 검사 분할에서 모델이 얼마나 강력한지 나타낸다.
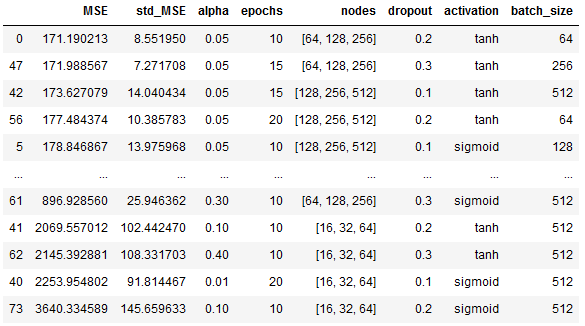
The final model
alpha = 0.05
epochs = 10
specific_lags = [1,2,3,4,5,10,20]
nodes = [64, 128, 256]
dropout = 0.2
activation = 'tanh'
batch_size = 64
returns:
train set RMSE:12.82085148416833, R2:0.9061075756420954
test set RMSE:25.352943890689797, R2:0.7777536332595578
lag, number of layers, optimizer, learning rate를 조정하면 더 좋은 RMSE를 구할 수 있을 것이다.
