원문

세계 좌표의 3D body pose에서 joint angle을 계산하는 전략

• 한 벡터를 다른 벡터로 회전시키는 rotation matrix
• rotation matrix를 major axes(축)에 따라 rotation sequence로 분해 (ex ZXY, XYZ rotation)
• T pose 셋업

Obtaining a rotation matix that rotates one vector to another

AXB 즉 normal direction(법선 벡터)를 통해 general vector A를 B로 회전시킬 수 있다. 그 다음, 좌표를 A, B, AXB basis으로 회전한 후, 원래의 basis로 다시 회전한다

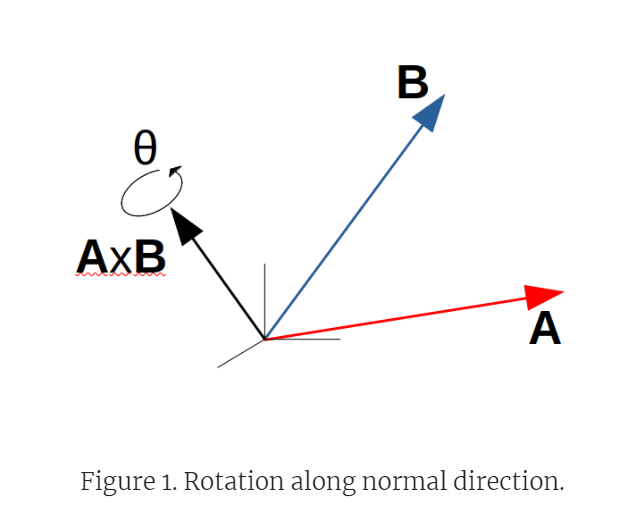
새 basis는 A를 unit vector로 만들고 B의 rejection을 A에 취해(rejection이 뭔지 모르겠음 본문에는 taking the rejection of B onto A라고 하고, 코드 상으로는 v = uB - np.sum(uA uB)uA 이 부분인듯)두번째 축을 구한다. 세번째 축은 AXB의 normalized로 정의한다. 이는 basis rotation matrix의 변화를 기록할 수 있게 해준다.

좌표가 정렬되면 Rz rotation matrix로 주어진 AXB(법선 벡터) 방향으로 간단하게 회전할 수 있다. rotation angle은 알 필요 없는데, cos(theta)와 sin(theta)가 정규화된 A와 B 벡터의 dot / cross products이기 때문. 또한 정규화를 하기 때문에 벡터의 길이가 같을 필요도 없다

#calculate rotation matrix to take A vector to B vector
def Get_R(A,B):

    #get unit vectors
    uA = A/np.sqrt(np.sum(np.square(A)))
    uB = B/np.sqrt(np.sum(np.square(B)))

    #get products
    cos_t = np.sum(uA * uB)
    sin_t = np.sqrt(np.sum(np.square(np.cross(uA,uB)))) #magnitude

    #get new unit vectors
    u = uA
    v = uB - np.sum(uA * uB)*uA
    v = v/np.sqrt(np.sum(np.square(v)))
    w = np.cross(uA, uB)
    w = w/np.sqrt(np.sum(np.square(w)))

    #get change of basis matrix
    C = np.array([u, v, w])

    #get rotation matrix in new basis
    R_uvw = np.array([[cos_t, -sin_t, 0],
                      [sin_t, cos_t, 0],
                      [0, 0, 1]])

    #full rotation matrix
    R = C.T @ R_uvw @ C
    #print(R)
    return R

Decomposing rotation matrix into rotation sequence along major axes

rotation matrix를 분해할 때는 rotation의 순서가 중요하다. 아래 예시에서는 ZXY 순서를 사용하며 이는 먼저 Y를 중심으로 회전한다. ZXY의 rotation matirx는 아래와 같다.

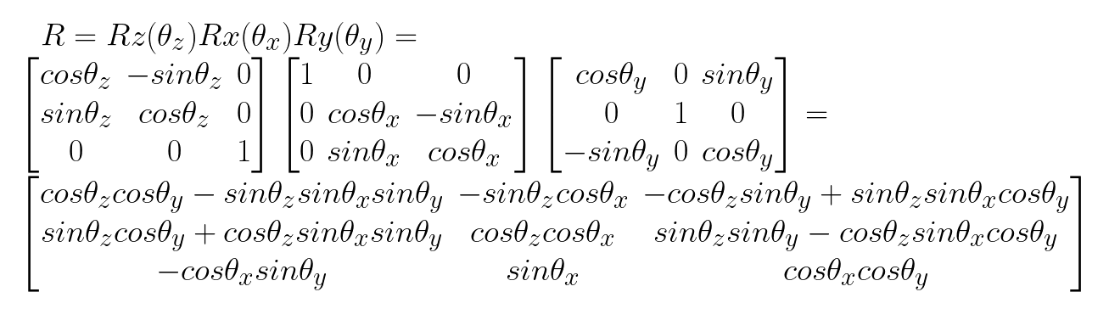
위를 통해 모든 rotation angle을 계산할 수 있다. 예를 들어 arctan(r01/r11)는 z축을 기준으로 하는 회전을 준다. 만약 다른 회전 순서가 사용된다면 행렬은 올바른 순서로 다시 작성되어야하며 joint angle도 다시 구해야한다.

추가적으로 arctan 함수는 quadrant를 확인해야한다. Numpy에 quadrant를 확인하는 관련 함수가 있다.

위를 통해 모든 rotation angle을 계산할 수 있다. 예를 들어 arctan(r01/r11)는 z축을 기준으로 하는 회전을 준다. 만약 다른 회전 순서가 사용된다면 행렬은 올바른 순서로 다시 작성되어야하며 joint angle도 다시 구해야한다. 

추가적으로 arctan 함수는 quadrant를 확인해야한다. Numpy에 quadrant를 확인하는 관련 함수가 있다.

Define a T pose

초기 포즈를 정의하고 각 joint에 축을 붙이는 방법은 많다. 가장 쉬운 것은 T pose를 초기 포즈로 정의하고 z축이 forward를 향하도록 각 joint에 축을 배치하는 것이다. 리프 노드 즉 end point의 경우 축을 가질 필요가 없다. 각 joint는 부모의 rotation matrices만을 사용한다.

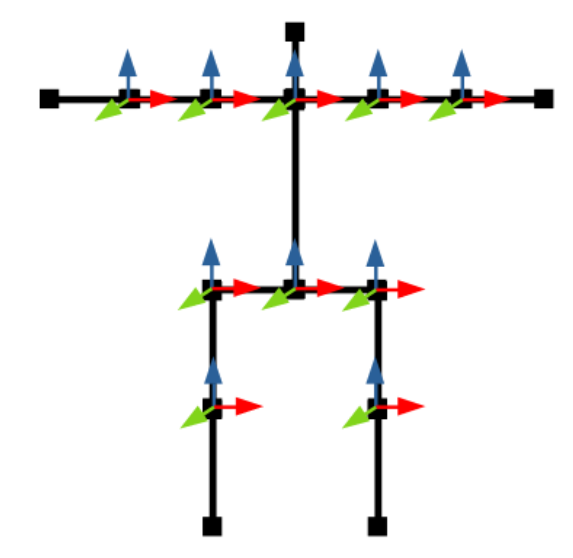
hip의 중간 포인트가 일반적으로 root joint로 정의되며 모든 것은 이에 관련되서 정의된다. 예를 들어 왼쪽 hip은 length x(1,0,0) vector, 왼쪽 무릎은 length x(0,-1,0) vector로 정의될 것이다. 모든 joint는 root joint가 아닌 축에 의해 정의되어야 한다.

joint의 position을 계산하려면 모든 부모 joint의 position을 계산해야한다. 따라서 chain of matrix multiplication을 사용한다. 예를 들어 발의 world position을 계산하려면 다음과 같다

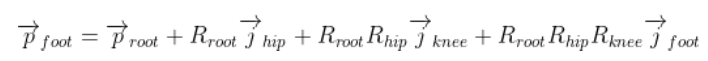
여기서 j vector는 direct parent에 대한 각 뼈의 offset이다. 이를 통해 세계 공간에서의 joint position을 얻고 joint angle을 계산하는 것이다.

Calculating Joint Angles

각 joint의 world position만 주어졌고 joint angle을 구해야한다고 가정하자. root joint를 결정하고(이때 root joint는 보통 center of the hips) 그 다음 root joint의 rotation을 결정해야한다. 즉, root joint에 축을 배치해야한다. 이는 왼쪽 hip을 x축 방향, 목을 y축 방향으로 선택해서 정한다. z축은 이 둘의 cross product이다. root joint의 단위 벡터를 정의한 후 세계 좌표계의 zero point(0,0,0)에 위치시키고 T pose와 일치하도록 회전시킨다.

def get_hips_position_and_rotation(frame_pos, root_joint = 'hips', root_define_joints = ['lefthip', 'neck']):

    """
    frame_pos is a dictionary that contains the current world space position of each joint.
    The root joint is named "hips" here and is the center between the left and right hip positions.
    We can define the x axis as vector pointing from 'hips' to 'lefthip'.
    We can define the y axis as vector pointing from 'hips' to 'neck'.
    """

    #root position is saved directly
    root_position = frame_pos[root_joint]

    #calculate unit vectors of root joint
    root_u = frame_pos[root_define_joints[0]] - frame_pos[root_joint]
    root_u = root_u/np.sqrt(np.sum(np.square(root_u)))
    
    root_v = frame_pos[root_define_joints[1]] - frame_pos[root_joint]
    root_v = root_v/np.sqrt(np.sum(np.square(root_v)))
    
    root_w = np.cross(root_u, root_v)

    #Make the rotation matrix
    C = np.array([root_u, root_v, root_w]).T
    
    #calculate the angles representing the root joint rotations.
    thetaz,thetay, thetax = utils.Decompose_R_ZXY(C)
    root_rotation = np.array([thetaz, thetax, thetay])

    return root_position, root_rotation

root position과 root rotation angle을 알고있다면 각 joint anlge을 구할 수 있다. 간단하게 하기 위해서 모든 joint position에서 root position을 빼서 세계 공간 중심에 오도록한다. joint angle을 계산하기 위해서 root joint에 가까운 joint부터 시작한다. 예를 들어 왼쪽 hip의 rotation matrix를 알고싶다면 무릎의 joint position을 사용해야한다.

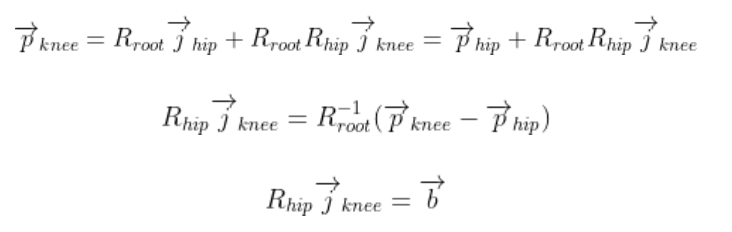
p는 관절 좌표, j는 부모 관절 축으로부터의 관절 offset이다. rotation matrix의 inverse는 transpose이다. 마지막 식은 vecjor j에서 vector b로의 회전을 나타낸다. 위의 Get_R() 함수를 호출해서 joint angle의 회전을 구할 수 있으며 roation matrix을 얻게 되면 joint angle을 구하기 위해 분해 함수를 호출한다

R = Get_R(j, b)
thetaz, thetax, thetay = Decompose_R_ZXY(R)

예를 들어 무릎의 roation matrix를 얻으려면 다음과 같다.

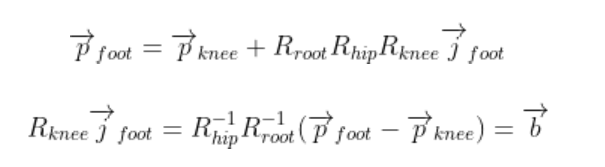
Closing remarks

보통 joint angle은 angle limit과 pose setup에 따라 고유하지 않기에 모델 학습에 좋지 않은 정보 인코더이다. 그러나, 포즈를 표준 골격으로 retargeting하는데 유용한데 예를 들어 대상마다 신체 비율이 다르기에 동일한 동작이어도 세계 좌표는 달라진다. 이를 해결하기 위해 joint anlge을 계산하고 이를 표준 골격에 넣어 해결할 수 있다. 또는 3D 좌표를 얻기위해 keypoint를 추정했으나 부정확성으로 일관성이 없을 때 사용할 수 있다.