Stacked DCNN

먕먕·2022년 5월 18일

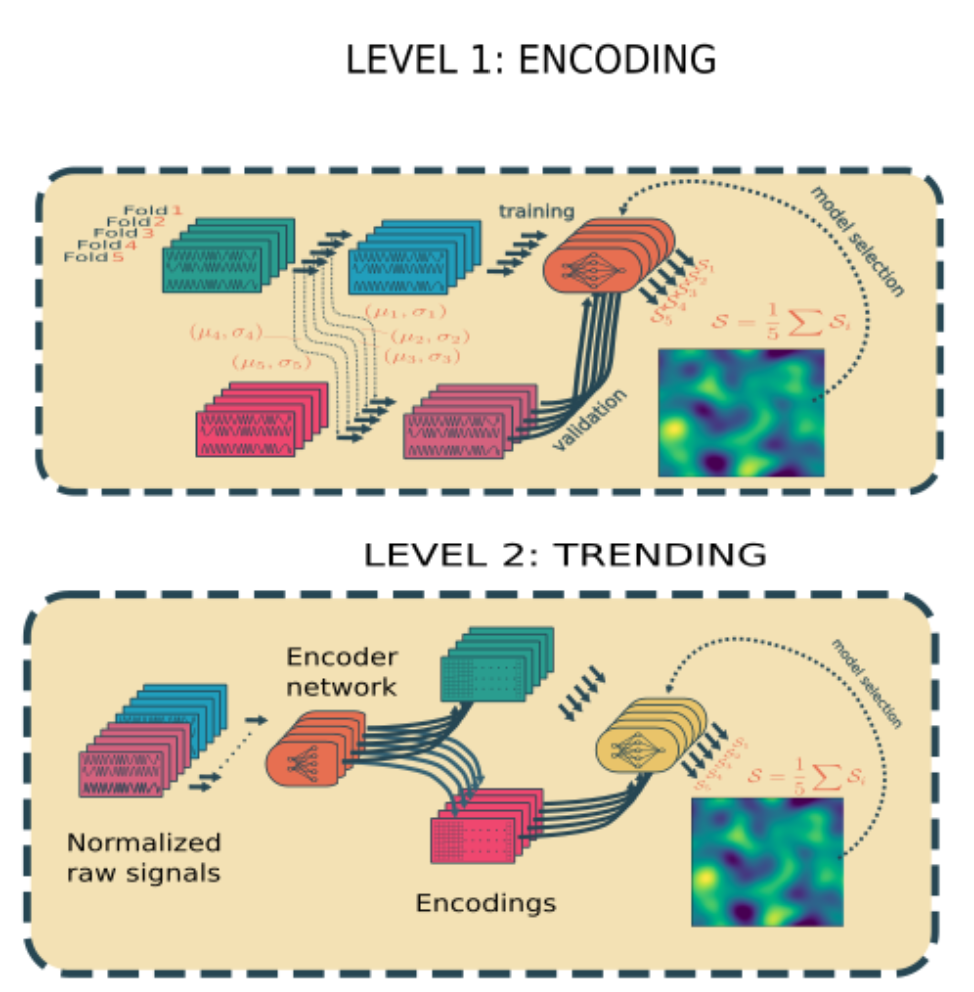
Level 1 : encoding 차원을 감소시키고 노이즈를 삭제
Level 2 : trending 인코딩으로 생성된 signal의 경향을 학습한다

서로 다른 모형을 개발하는 데 사용되는 20개의 변수는 서로 다른 scale를 가진다. 그러한 이유로, 제안된 네트워크에 그러한 데이터를 직접 공급하면 모델의 학습과 수렴이 느려진다. 따라서, 훈련 단계 전에, 변수를 공통 척도로 균질화하기 위해 데이터 정규화 단계가 필요하다.(표준 정규화)

평균과 분산은 각 훈련 교차 검증(cross-validation) 세트에 대해 계산되며 validation 세트를 정규화하는 데에도 사용된다.

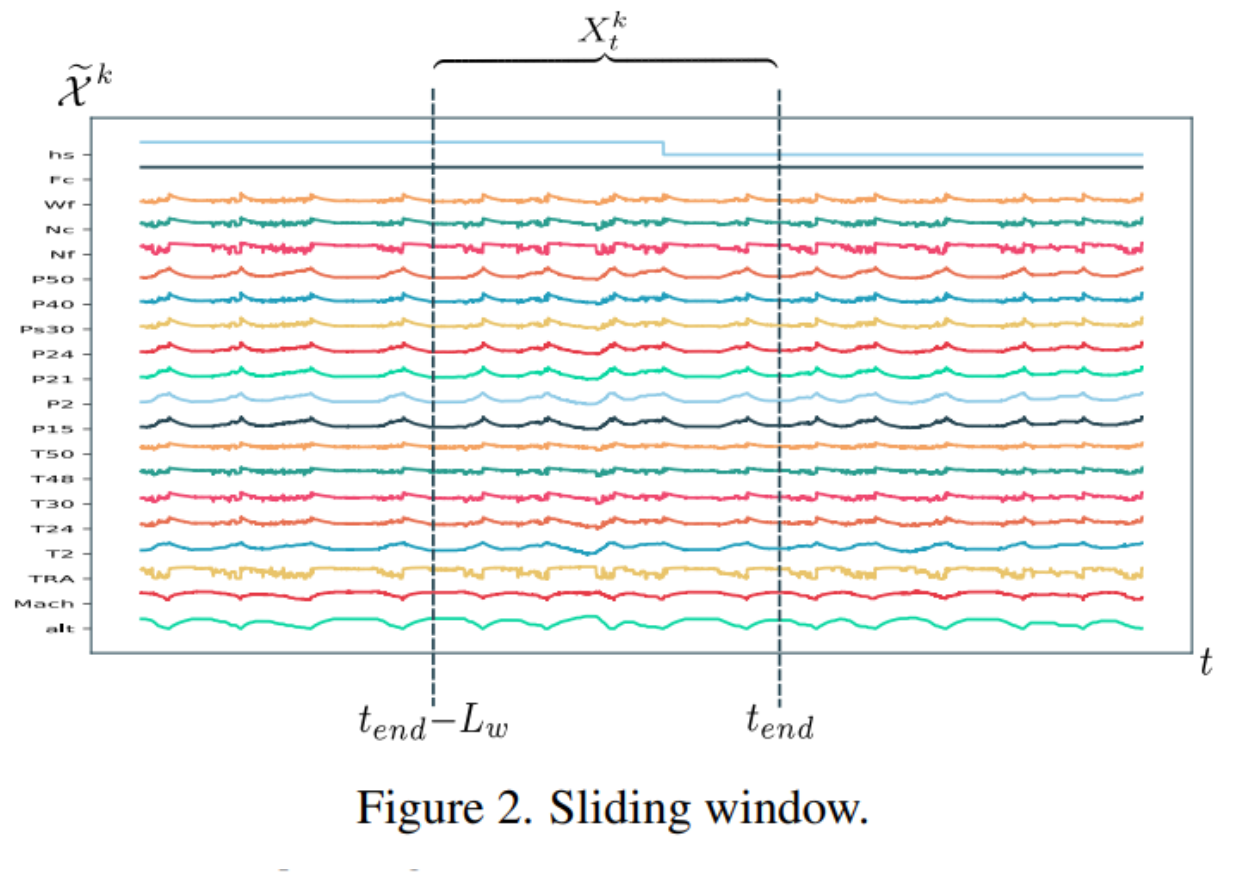
정규화된 데이터를 time window를 통해 sliding하면서 네트워크 인풋을 생성한다
즉 시계열 예측을 지도 학습으로 바꾸는 방법이다.

Level 1
인코딩이 필요한 이유 : raw input의 높은 차원을 감소시키기 위해 사용 + 노이즈 제거

여기서 DCNN을 사용한다
DCNN = 심층 컨볼루션 신경망

convolution : 파라미터 공유 및 로컬 수신 필드 구현
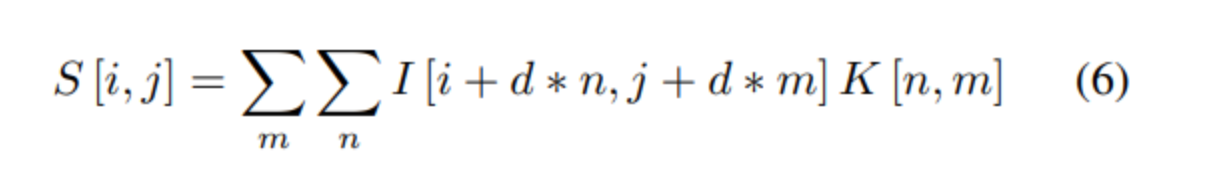
polling : 다운 스케일링 수행.
피처 맵이 축소되었기 때문에 상위 레이어에 대한 계산 요구 사항을 줄이고, 완전히 연결된 상위 레이어에 대한 연결 수(parameter)를 줄이고, 공간 변환 불변성의 형태를 제공하며, 과적합 위험을 완화하는 데 도움이 된다.

Level 2
위의 값을 input으로 받고 FC layer를 사용해 RUL의 regression 진행

교차 검증 : train set을 train+validation으로 분리하고, validation으로 검증한다
K-Fold Cross Validation : 회귀 모델에 사용. 데이터가 독립적이고 동일한 분포를 가진 경우 사용.

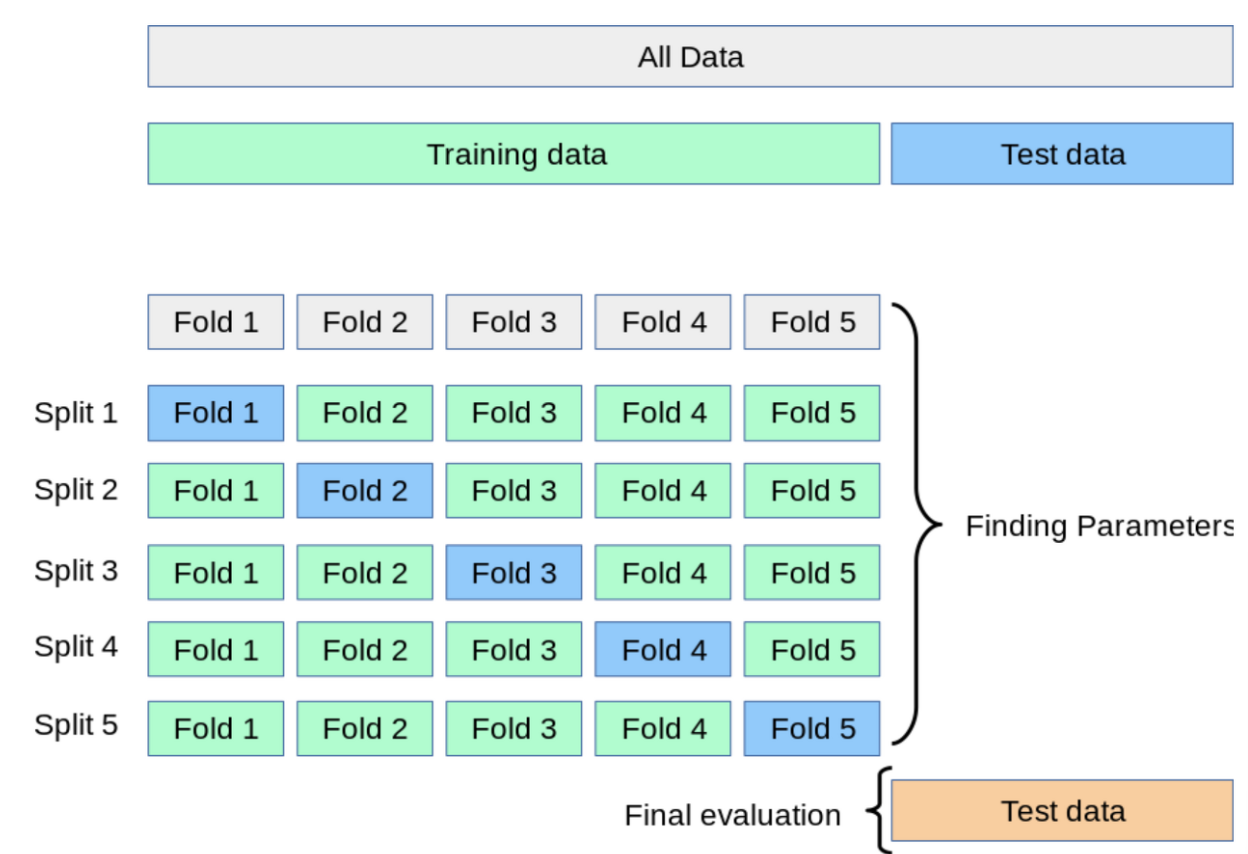
총 k 개의 성능 결과가 나오며, 이 k개의 평균을 해당 학습 모델의 성능이라고 한다.

베이지안 최적화와 RMSE loss를 사용하여 training한다. (RMSE 사용하는 이유 : NASA의 score는 미분 불가해서) 또한 early stop를 사용함

여기도 DCNN을 사용한다

0. Abstract

제시된 솔루션은 두 가지 레벨로 쌓인 두 개의 심층 컨볼루션 신경망(DCNN)을 기반으로 한다.
첫 번째 DCNN은 정규화된 raw 데이터를 입력으로 사용하여 저차원 특징 벡터를 추출하는 데 사용된다.
두 번째 DCNN은 이전 DCNN에서 추출한 벡터 목록을 수집하여 RUL을 추정한다.
모델 선택은 반복적인 무작위 하위 샘플링 검증 접근법을 사용하여 베이지안 최적화를 통해 수행되었다.

1. Introduction

최종 목표는 시스템 수명 중 임의의 시점에서 시스템 작동 조건이 주어졌을 때 이러한 고장이 발생하거나 열화 수준에 도달할 때까지 남은 시간을 추정하는 것이다. RUL 추정을 위한 두 가지 주요 방법론인 모델 기반 방법과 데이터 기반 방법을 문헌에서 찾을 수 있다.
모델 기반 방법 : 물리 및 통계를 기반으로 열화 모델을 설정하여 시스템의 열화 추세를 예측. 각 특정 구성 요소 및 고장 유형의 물리적 거동에 대한 강력한 지식이 필요하므로, 점점 복잡해지는 현재 시스템(Z)을 위한 모델을 개발하기가 어렵다. 모델에 대해 일부 가정을 해야 하므로 편향될 수 있다. 제한된 예측 성능을 가지며 각 다른 유형의 기계에 대해 임시로 설계되어야 한다.
데이터 기반 방법 : 사전 전문 지식이 필요하지 않다. 기계 학습 알고리듬을 사용하여 과거 상태 모니터링 데이터를 사용하여 시스템의 성능 저하 추세를 학습한다.

2. Data and Problem Description

CMAPSS data set은 이미 성능이 저하된 시스템에서 샘플만 추출하여 구축되었다. "따라서 fault의 발단은 예측될 수 없습니다. fault의 진전만이 예측됩니다."
N-CMAPSS는 fault가 발생할 때까지 건강한 상태로 시작하는 궤적의 전체 이력을 제공한다.
엔진의 모든 회전 구성 요소(팬, LPC, HPC, LPT 및 HPT)는 열화 프로세스의 영향을 받을 수 있다. 이 모델은 다음과 같은 비선형 시스템으로 정의된다. 여기서 xs는 물리적 특성, xv는 관찰되지 않은 특성, w는 시나리오 설명자 작동 조건, θ는 건강 모델 매개 변수이다.
7가지 고장 모드가 정의, 비행 길이에 따른 세가지로 나눈 비행 등급. 센서 출력 Xs, 시나리오 설명자 W 및 보조 데이터 A를 사용하여 시스템의 남은 내용연수 Y를 예측할 수 있는 모델 G의 개발을 중심으로 전개된다.

3. Proposed Methology

* Data normalization

20개의 변수는 서로 다른 척도를 가진다. 제안된 네트워크에 이러한 데이터를 직접 공급하면 모델의 학습과 수렴이 느려진다. 따라서 training 이전에 변수를 공통 척도로 균질화하기 위해 데이터 정규화 단계가 필요하다. 표준 정규화가 사용된다. 평균과 분산은 각 훈련 교차 검증 세트에 대해 계산되며 검증 세트를 정규화하는 데도 사용된다.

* Time window processing

정규화 이후, 네트워크의 입력은 정규화된 데이터를 통해 슬라이딩 타임 윈도우를 사용하여 생성된다. 실험 초기에 constant RUL을 설정하는 것이 일반적이지만, 이 연구에서는 이러한 종류의 가정이 모델에 편견을 도입할 수 있기 때문에 이 접근 방식을 따르지 않았다. 대신 ground-RUL lael을 각 unit Y의 RUL의 cycle의 선형함수로 설정했다.

* Level1 and Level2 model : Convolutional Neural Networks

Level1에서의 목표는 raw input signal의 time-windowed 인코딩에 좋은 모델을 찾는 것이다. 이 인코딩은 input data의 높은 차원때문에 필요하다. 인코딩의 또 다른 목표는 차수 감소 외에도 노이즈를 제거하는 것이다.
Level2에 위의 입력이 들어온다. 목표는 RUL의 추정치를 제공하는 것이다.
두 level 모두 DCNN(심층 컨볼루션 신경망)이 선택된다. CNN은 parameter sharing 및 subsampling을 사용하여 가장 중요한 로컬 특징이 있는 피쳐 맵을 추출한다. DCNN의 주요 작업은 컨볼루션과 풀링이다.
컨볼루션은 parameter sharing과 local receptive field를 구현한다. Kernel matrix는 input matrix를 지나가며 어느 곳에나 존재하는 패턴을 찾는다. FCN과 비교하면, overfitting의 가능성과 가중치의 개수가 줄어든다.
풀링은 이전에 직사각형 풀링 영역으로 분할된 입력의 각 영역에 통계 연산을 적용하여 다운스케일링을 수행한다. feature map이 다운스케일링 되기 때문에 upper layer에 대한 계산 요구 사항을 줄이고, 연결된 upper layer에 대한 매개 변수를 줄이며, spatial transformation invariance의 형태를 제공하고, overfitting 위험을 완화하는 데 도움이 된다.

* Cross validation

신경망은 조정해야 할 매개 변수의 수가 많다. 또한 슬라이딩 윈도우의 크기 또한 최적화되어야 한다. k-폴드 교차 검증은 k(폴드 수)가 증가할수록 검증 세트의 크기가 감소한다는 단점이 있다. 이 문제를 해결하는 k-fold repeated random subsampling validation 과 같은 대안이 있다.
이 연구에서 k = 5와 훈련 세트의 30%인 검증 접이식 크기, 즉 총 90개에서 27개의 무작위 단위를 사용하여 이후의 전략이 선택되었다.

* Model Selection

모델 선택 단계의 목표는 각 모델에 대한 최적의 매개 변수 구성을 얻는 것이다. 이를 위해 베이지안 최적화를 최적화 전략으로 선택했다. 모델은 손실 함수로 RMSE를 사용하여 훈련되었다. 그러나 베이지안 최적화가 테스트할 다음 모델 매개 변수 set을 결정하기 위해 사용하는 손실 함수는 score S이다.(RMSE와 Nasa's scoring function의 average)
Early stopping 방법이 모델 훈련 과정을 끝내는 시그널로 사용되었다.

4. Experiments and Results

최적의 모형을 찾는 데 사용되는 설정 및 매개변수에 대해 설명한다. 각 level의 결과들을 비교하고 최종 솔루션을 설명한다. 마지막으로 hidden test data에 적용한다.

* Level1 : encoding

Level 1의 encoding 모델의 목표는 raw 시그널에 대한 차원 감소와 노이즈 감소를 수행하는 것이다. 이를 위해 DCNN이 사용되었다. DCNN은 두 부분으로 나눌 수 있다.
첫 부분은 convolution과 pooling layer로 구성된 Nb 블록의 스택이다. 이 첫 부분의 목표는 task에 잠재적으로 유용한 특징을 추출하는 것이다.
두번째 부분은 fully connectedd layer들로 구성되어 있으며 이 경우 RUL의 회귀 분석을 한다. 최적의 하이퍼 파라미터 구성을 얻기 위해 Bayesian optimization이 100회 반복동안 실행된다. 처음 10회 반복은 무작위로 선택된 하이퍼 파라미터들로 모델이 구성된다. 이들은 error surface의 초기 추정을 생성하는 베이지안 프로세스에 사용된다. 10회 반복 이후 최적화 프로세스는 테스트 할 가장 유망한 하이퍼파라미터에 베이지안 규칙을 적용한다.
차트에서 볼 수 있듯이 고장이 더 일찍 발생할 경우 모형의 신뢰성이 더 높아진다. 첫 번째 주기에서 예측은 모형이 하강 추세를 포착할 수 있을 때까지 거의 일정한 것으로 보인다.

* Level2 :

Level 2의 목표는 최종 RUL 예측을 수행하는 것이다. 이 모델의 입력은 level 1모델에서 생성된 raw input의 인코딩이다. 따라서 fold 별 train과 test set의 인코딩을 생성하려면 첫 단계가 필요하다.
인코딩은 100개의 뉴런으로 구성된 두 번째 full connected layer에서 추출된다. 후보 level 2 모델에 대한 각 샘플 입력은 인코딩 위의 슬라이딩 윈도우를 사용하여 생성된다. 인코딩은 raw 신호의 차원 축소 버전이기 때문에 level 2 모델은 모델의 수용 영역을 확장하고 시간에 따른 추세에서 학습할 수 있다. 매개 변수 단계는 인코딩 간의 간격(초)을 정의한다.
그림 6은 모델의 입력 정보를 얻는 방법을 보여준다. Image channel은 입력을 구성하는 데 사용된다. 각 채널에는 100개의 벡터 인코딩이 있다. 따라서 입력의 총 인코딩 수는 100 · chanells이다.
레벨 2 모델도 DCNN이다. 최적화할 교차 검증 스키마와 파라미터 범위는 레벨 1 모델에서 동일하게 고려된다. 또한 이 L2 모델 최적화에서는 fc2, step 및 channel의 세 가지 매개 변수를 추가로 고려해야 한다. 매개 변수의 구성은 level 1과 level 2가 상당히 비슷하다. Level 1 하이퍼 파라미터가 시드로 최적화 프로세스에 제공되기 때문이다. 훈련 및 정규화 매개 변수에만 차이가 있다. 나머지 아키텍처는 동일합니다.
추가 파라미터와 관련하여 파라미터 단계에서 선택한 값이 989라는 점이 흥미롭다. 레벨 1 모델은 RUL에 대한 상당히 좋은 추정치를 제공하기 때문에, 레벨 2 모델은 trend를 포착하고 RUL을 개선하기 위해 희소 인코딩 집합만 필요하다. 이 모델의 교차 검증 점수는 3.44이지만 앙상블 점수(즉, 점수를 계산하기 전에 예측의 평균을 취함)는 2.95이다. 교차 검증 점수와 앙상블 예측 사이의 이러한 차이는 모델의 예측이 좋은 수준의 비상관성을 가지고 있다는 것을 의미한다.
그림 7(아래)은 수준 2 모형의 예측 및 신뢰 구간을 보여준다. 이를 레벨 1 모델(그림 7 상단)과 비교하면, 적층 모델의 예측이 매끄럽고 향상되었음을 알 수 있다. 그림 8은 실측 자료 규칙과 각 적층 모델에서 획득한 점수 사이의 관계를 보여준다. 마지막으로, 그림 9는 각 클래스의 각 모델의 성능을 보여준다. 비행이 짧을수록 모형이 더 잘 수행된다는 점에 유의하자. 마찬가지로, 레벨 2 모델 성능의 개선은 짧은 비행의 경우 더 높다.

RUL prediction on test data
일반적으로 모델의 성능을 검증하기 위해서는 훈련 세트의 일부를 최종 테스트 세트로 저장해야한다. 따라서 train/validation 세트의 샘플 수가 감소한다.
여기서는 폴드 당 훈련된 모든 모델을 ensamble로 사용하는 것으로 구성된다. 2가지 이점이 있다. 교차 검증을 통해 최종 ensamble 모델 성능에 대한 신뢰 메트릭을 얻을 수 있다. 또한 최종 평균 예측의 신뢰 구간을 생성하기 위해 표본당 예측을 사용할 수 있다는 것이다.

5. Conclusions

시스템에 대한 전문적인 지식 없이 RUL을 추정하기 위한 강력한 방법론을 노출했다. 본 연구에서는 최종 솔루션을 얻는 과정을 두 가지 학습 단계로 나뉜다. 첫 번째에서 원시 데이터의 인코딩을 학습하고 두 번째 학습 단계의 입력으로 사용하여 RUL을 추정할 수 있는 최종 모델을 얻는다. 현재 솔루션의 여러 가지 가능한 개선 사항이 향후 연구의 대상이 될 것이다.
1) cycle에서의 RUL을 smoothing하면 오류 공간을 smooth 할 수 있으므로 학습 과정에 도움이 될 수 있다.
2) 제안된 방법론에서, 필요한 것보다 더 낮은 수의 사이클을 갖는 입력은 훈련 프로세스에서 제외되었다. 검증 세트의 경우, 이러한 입력은 초기 인코딩으로 채워졌다. 동일한 filling 을 적용하는 네트워크를 훈련하면 과적합을 줄이는 데 도움이 될 것으로 예상된다.
3) 또 다른 가능한 개선은 각 고장 유형이 각 유효성 검사 세트에 적절하게 표현되도록 훈련 접힘의 균형을 맞추는 것일 수 있다.
4) 인코딩 간 랜덤 gap을 사용하여 2 모델을 교육하라. 이를 통해 훈련 세트를 확장하고, 신뢰 구간을 계산하는 추가 메커니즘을 가지며, 최종 평균화된 RUL을 계산하기 위한 예측 수를 늘릴 수 있다.
5) 마지막으로, class과 health state features가 얼마나 예측적인지를 연구하는 것은 흥미로울 것이다.