VAE & GAN
VAE
What is VAE?
- Latent variable z 의 분포를 추정하고 이를 통해 원래 데이터의 분포를 예측하는 확률 모델(probability model)
- 기존의 Variational Bayes 의 mean field 접근 방식의 intractability 문제를 개선한 SGVB(Stochastic Gradient Variational Bayes)를 optimization 방식으로 사용
- Marginal likelihood 에서의 lower bound (ELBO)를 최대화 (Gradient Ascend) 하며 parameter를 학습 → SGVB를 활용한 Auto-Encoding Variational Bayes
Keywords
- Marginal Likelihood:
- 모델 파라미터에 대한 분포(prior distribution)가 주어졌을 때 관측되는 데이터의 확률
- KL-divergence와 lower bound의 합으로 표현
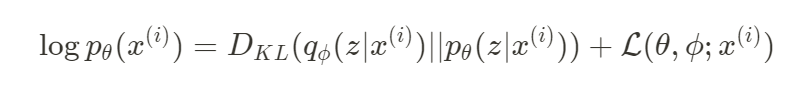
- KL-Divergence : 두 분포 간의 차이를 나타내는 지표, 언제나 0보다 크거나 같은 값
- VAE의 marginal likelihood에서는 true posterior와 approximate posterior의 차이
- Sampling:
- 주어진 input data x로부터 encoder를 통해 추출한 feature(z)를 latent variable space에 mapping 시키는 것
- Approximate Posterior:
- Latent variable z 의 분포
- VAE의 encoder부
- VAE의 궁극적 목표는 실제 데이터의 분포에 가까운 확률 분포를 찾는 것으로, 이를 위해 approximate posterior를 실제 posterior에 가까운 값을 찾는 것은 매우 중요
Method
-
Reparametrization Trick
- 은 평균 , 표준편차 의 분포를 따르는데, 이것을 sampling 하는 대신 표준 가우시안 분포를 따르는 를 sampling ()
- sampling 한 후에는 scale & shift 해서 원하는 평균과 표준편차를 구함
- intractablility 의 원인이 되었던 randomness를 다른 파라미터들()로부터 분리
-
Variational Bound
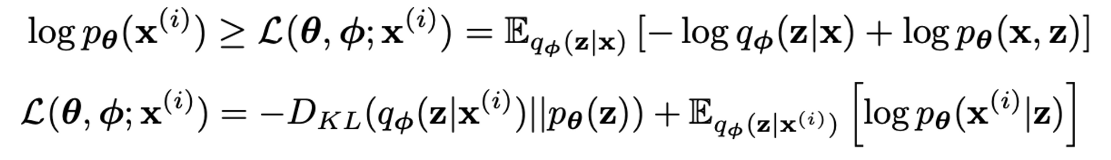
-
Apply Reparametrization

Conclusion
- SGVB는 variational lower bound의 이상적인 estimator
- continuous latent variable에 대한 효과적인 approximate inference가 가능
- AEVB는 SGVB를 활용한 optimization 알고리즘으로, 효과적인 inference와 학습이 가능
VAE 세줄 요약
- 확률 모델은 데이터의 분포를 구하는데 의의를 갖고, 이를 학습하는데 marginal likelihood에 최대한 가까워지는(최대한 큰) lower bound를 구해야함
- 하지만 lower bound는 approximate posterior와 더불어 직접적으로 계산해내기 겁내 어렵고, 이걸 intractable 하다고 표현함
- 이걸 해결하기 위해서 논문에서는 reparametrization trick 을 활용한 SGVB라는 gradient ascend 방식을 제안했고, SGVB를 이용한 optimization 알고리즘을 AEVB라고 함
GAN
Overview
생성 모델을 훈련하기 위해 적대적인 과정을 사용하는 새로운 프레임워크
G : 데이터 분포를 잡아내는 생성 모델
D : 샘플이 G가 아닌 훈련 데이터에서 나왔을 확률을 추정하는 판별 모델
생성 모델 G와 판별 모델 D 두 개를 동시에 훈련시킨다. G의 훈련은 D가 실수를 저지르도록 하는 확률을 최대화하는 방향으로 이루어진다. 즉 G가 훈련 데이터 분포를 복원하고 D가 모든 상황에서 1/2인 유일한 해가 존재한다. 다층 퍼셉트론으로 G와 D를 정의된다면, 역전파 알고리즘을 사용하여 전체 시스템을 훈련시킬 수 있다.
Value Function
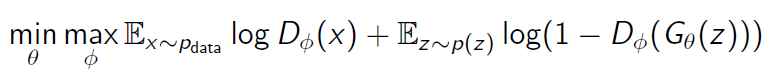
1을 실제 데이터, 0을 가짜(생성) 데이터라고 label을 부여
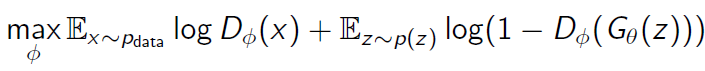
판별기는 D(x)를 1에 가깝게, D(G(z))를 0에 가깝게 만들어 위 식을 최대화하는 것을 목표로 한다. 즉 실제 데이터 x를 실제 데이터로, G(z)를 가짜(생성)데이터로 판별하도록.
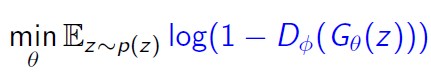
생성기는 D(G(z))를 1에 가깝게 만들어 위 식을 최소화하는 것을 목표로 한다. 즉 G(z)가 실제 데이터로 판별하도록.
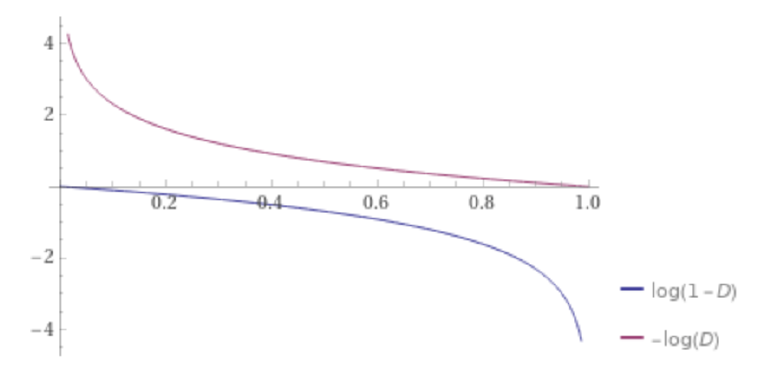
이때, 생성기의 성능이 좋지 않다면 log(1-D) 즉 D(G(z))가 0에 가까울 때 gradient가 0에 수렴하여 학습이 잘 되지 않는다. 따라서 아래 식을 대신 사용한다

Process Flow

pdata : training data의 분포
pg(G(z)) : G가 생성해낸 분포
D : D즉 판별기가 구분할 수 있는 확률

Limitation
training instability
두 개의 신경망을 경쟁시켜 학습하는데, 이 경쟁은 훈련 과정을 불안정하게 만든다. training epoch이 길어질 수록 oscilation이 발생하는 것으로, global optimum에 수렴하지 못함
mode collapse
G를 D를 업데이트하지 않고 너무 많이 훈련시키면 G가 너무 많은 z 값을 동일한 x 값으로 축소하여 충분한 다양성을 갖지 못해 pdata를 모델링하기에 충분한 다양성을 갖지 못하는 "Helvetica 시나리오”가 생긴다
즉 한 두 샘플과 비슷한 결과물만 생성되는 경우
evaluation
GAN의 성능을 객관적 수치로 표현할 수 있는 평가 지표 부재(GAN의 output이 새롭게 만들어진 데이터이므로 비교할 대상이 없음)
